基于RBF神經網絡-滑模觀測器的PMSM無傳感器矢量控制

(上海理工大學 光電信息與計算機工程學院,上海 200093)

永磁同步電機具有高功率密度和高效率的特點，因此被作為伺服電機廣泛應用于高動態性能和高密度場合[1]。

永磁同步電機矢量控制系統通常采用位置傳感器(如光電編碼器、霍爾傳感器)來獲取轉子位置，一方面增大了整個系統的體積，另一方面降低了整個系統的抗擾性，使其易因電磁干擾以及惡劣的環境條件產生故障，甚至危及操作者人身安全。無位置傳感器控制方案克服了這一缺陷，同時降低了成本，正在成為電機調速方法的重要研究方向。

在永磁無刷電機的無位置傳感器矢量控制方案中，準確的轉子實時位置信息尤為重要。PMSM的反電動勢包含了轉子位置和速度信息，因此基于反電動勢的估計方法被廣泛使用，如卡爾曼濾波法[1-2]、模型參考自適應法[3-4]、滑模觀測器法[5]。其中滑模觀測器法具有結構簡單、魯棒性強、對參數不敏感等特性，因此常被實際應用于PMSM的驅動控制中。

然而，滑模變結構方法因其時間和空間的滯后特性將會使系統產生抖振現象，估算結果含有高頻振蕩噪聲。并且，為了實現估計誤差的快速收斂以及滿足Lyapunov穩定性條件，滑模變結構方法中的切換增益需要足夠大，繼而加劇了抖振現象[2]。

人工神經網絡(ANN)可以在不需要確定系統精確數學模型的前提下實現準確的狀態估計[8]。人工智能特點之一就是其學習過程。基于此，有一些方法直接將電機參數(如α-β坐標下的電流、電壓)作為神經網絡的輸入[9]，電機轉速或轉子位置作為神經網絡的輸出來實現永磁無刷電機的無傳感器控制。這種方法利用了神經網絡的自學習能力，但依賴電機數據采樣進行離線訓練，并且結構復雜，設計和調試難度大，難以應用到實際操作中。

為了減弱上述滑模觀測器在應用中的抖振問題，以及簡化基于神經網絡控制方案的系統結構，提出一種利用RBF神經網絡的自學習能力動態調節滑模觀測器的切換增益的方法，即設定神經網絡的輸入為傳統滑模估計方案中的電流估計誤差，輸出為滑模增益，從而使估計模塊能夠獲得更準確的位置和速度估計。為了避免神經網絡的離線訓練對訓練數據的依賴以至產生過擬合，同時降低學習的時間成本，并提高神經網絡在實時工作中的魯棒性，本文方法將網絡的學習和運行過程進行了結合，使得網絡參數能夠在工作過程中進行適時調整。分析及仿真實驗表明，該方案有效減弱了滑模變結構方法中的抖振現象，為電機的矢量控制提供更準確得轉子位置信息，保證了系統穩定性和魯棒性。

1 永磁同步電機的數學模型

永磁同步電機在靜止α-β坐標系下的數學模型為

(1)

其中，

(2)

式中,iα,β為相電流；uα,β定子電壓；Eα,β為反電動勢；R為繞組電阻；L為定子電感；ωe為電角速度。

2 無傳感器控制中的觀測器設計

2.1 基于滑模觀測器的靜子電流觀測器

基于上述PMSM模型的觀測器可以寫為

(3)

式(1)、式(3)兩式相減，可以得到電流誤差方程：

(4)

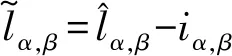
滑模控制律設計為

(5)

式中,KSW為滑模觀測器切換增益；sgn(x)為符號函數。

選擇滑模面為：

(6)

當觀測器狀態保持在滑模面上時，此時的控制量可以看作等效控制量。可得：

(7)

因此:

(8)

實際控制輸出量是一個有高頻擾動的不連續切換控制信號。因此，有必要添加一個額外的低通濾波器(LPF)來從中提取連續的反電動勢(back EMF)估計量。同時，基于估算公式(式(8))，還需要添加一個角度補償來彌補低通濾波器產生的相位延遲：

(9)

式中，ωc為低通濾波器的剪切頻率。并且，為減小抖振問題，采用sigmoid函數代替傳統的開關函數sgn(s)：

(10)

式中，a為可調參數。

2.2 觀測器穩定性分析

下面將由Lyapunov穩定性理論證明如下結論：系統在控制律(式(5))的作用下能夠在有限時間內達到滑模面(式(6))，并保證滑模面是漸進穩定的。

證明：定義Lyapunov函數：

(11)

其中，S(x)=[Sα(x)Sβ(x)]。則：

(12)

將式(3)、式(6)帶入式(12)并整理可得：

(13)

KSW>Max(eα,eβ)

(14)

因此，為了保證觀測器穩定，由RBF神經網絡輸出的增益KSW與α、β軸的反電動勢相比要足夠大。

3 RBF神經網絡-滑模觀測器

RBF神經網絡是一種三層前饋網絡，即輸入層、隱含層、輸出層，網絡結構簡單[11-13]。它也是一種局部逼近的網絡，且具有良好的泛化能力。把切換函數作為RBF網絡的輸入，滑模控制器作為RBF網絡的輸出，利用神經網絡的學習功能，可實現單輸入單輸出的神經滑模控制[8]，即用神經網絡動態調節滑模觀測器中的輸出切換增益。

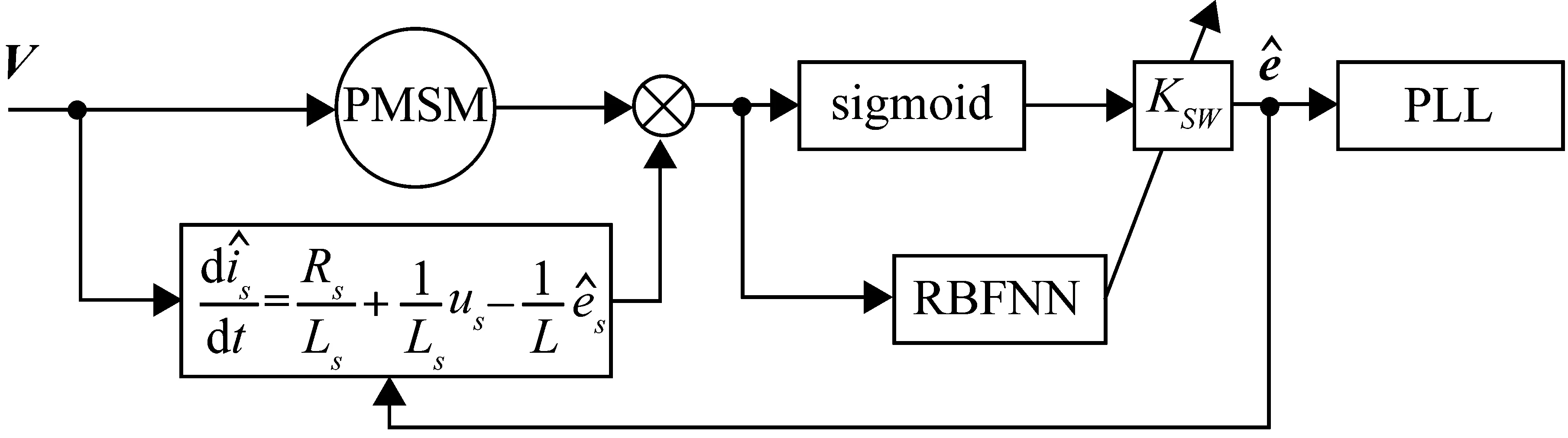
圖1 RBF神經網絡與滑模觀測器結構

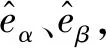
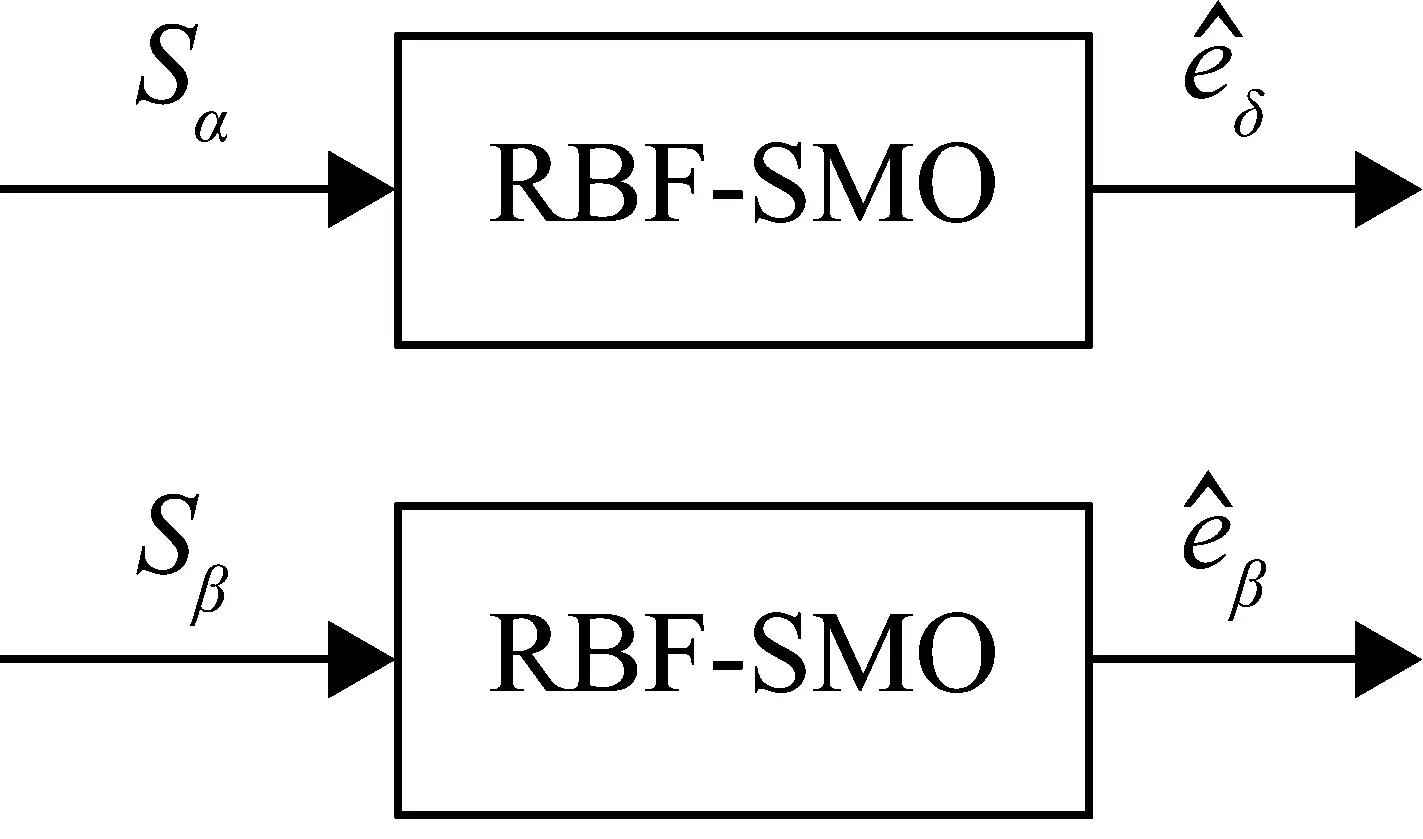
圖2 RBF網絡-滑模觀測器輸入和輸出

所設計的RBF神經網絡中，輸入層有一個參數，即電流誤差；隱層有5個神經元；輸出層有一個參數，即|KSW|。RBF神經網絡的初始權值隨機選定，工作過程中，每個神經元的輸出由前一層神經元對應的權值決定。

本文選擇高斯函數作為激勵函數：

(15)

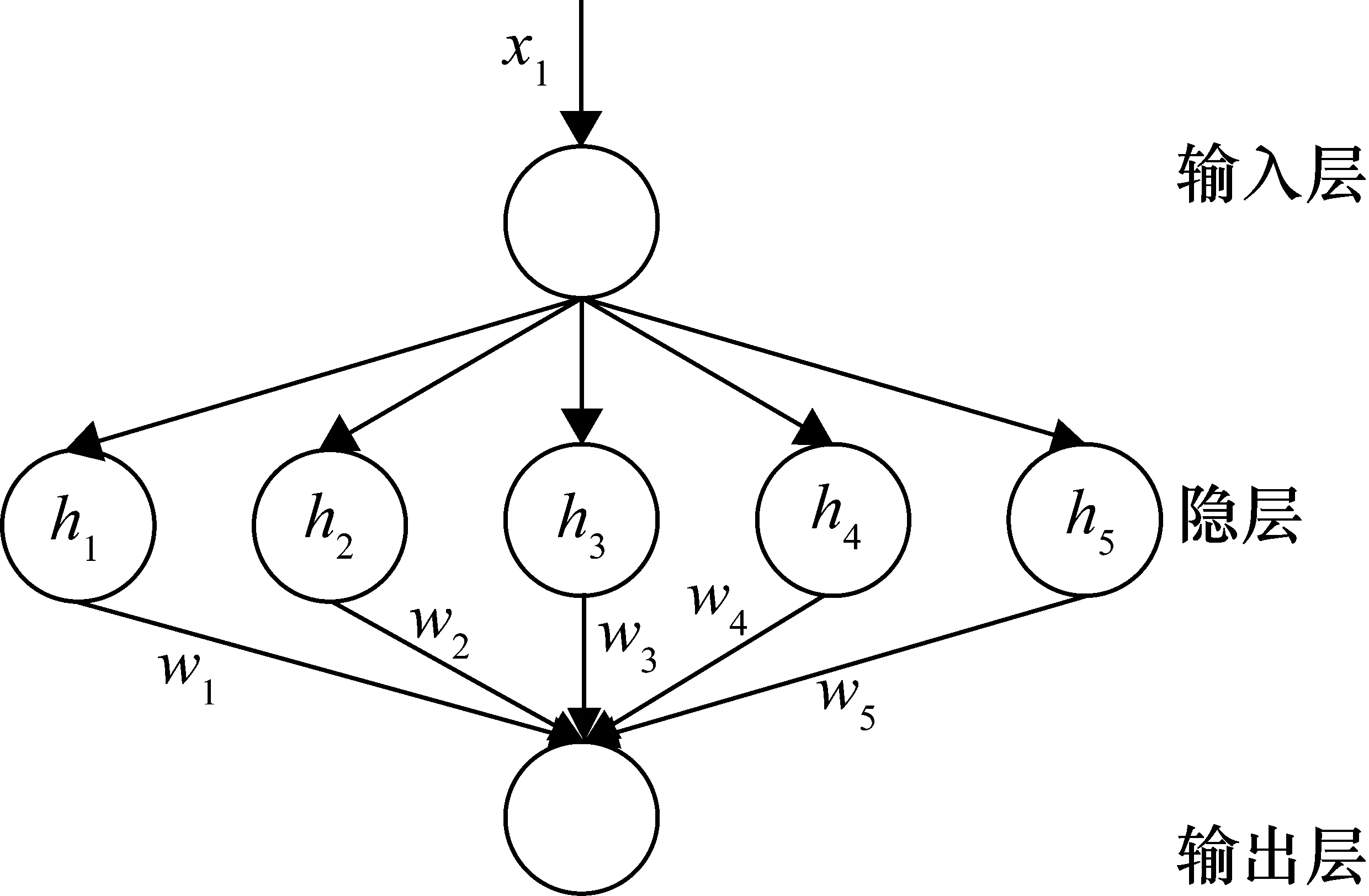
圖3 RBF神經網絡結構圖

式中，X即網絡輸入，徑向基函數向量為H=[h1,h2,…,h5]T，i即網絡隱含層第i個神經元，mi為神經元i的中心，σi為神經元i的寬度。

神經網絡輸出的絕對值是切換函數的增益：

K=|WTh(x)|

式中，WT為神經網絡權值;h(x)為高斯核函數輸出。

神經網絡中誤差函數選擇為

根據梯度下降理論，神經網絡的權值變化公式為

(16)

解之可得：

(17)

式中，C為常數。于是：

(18)

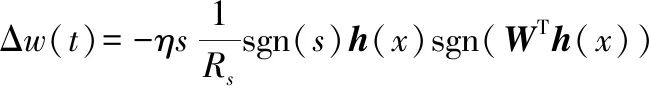
(19)

權值替換公式為：

w(t)=w(t-1)+Δw(t)+α(w(t)-w(t-1))

(20)

式中，α為慣性系數，α∈(0，1)；η為學習速率，η∈(0，1)。神經網絡通過以上權值更新公式實時、動態調節輸出增益，保證滑模面的漸進穩定性，使得估計的反電動勢更準確。

4 仿真結果及分析

為了驗證上述RBF-SMO方法的有效性，采用Matlab/Simulink仿真分析工具來建立永磁同步電機控制模型，控制框圖如圖4所示，電機相關參數見表1。

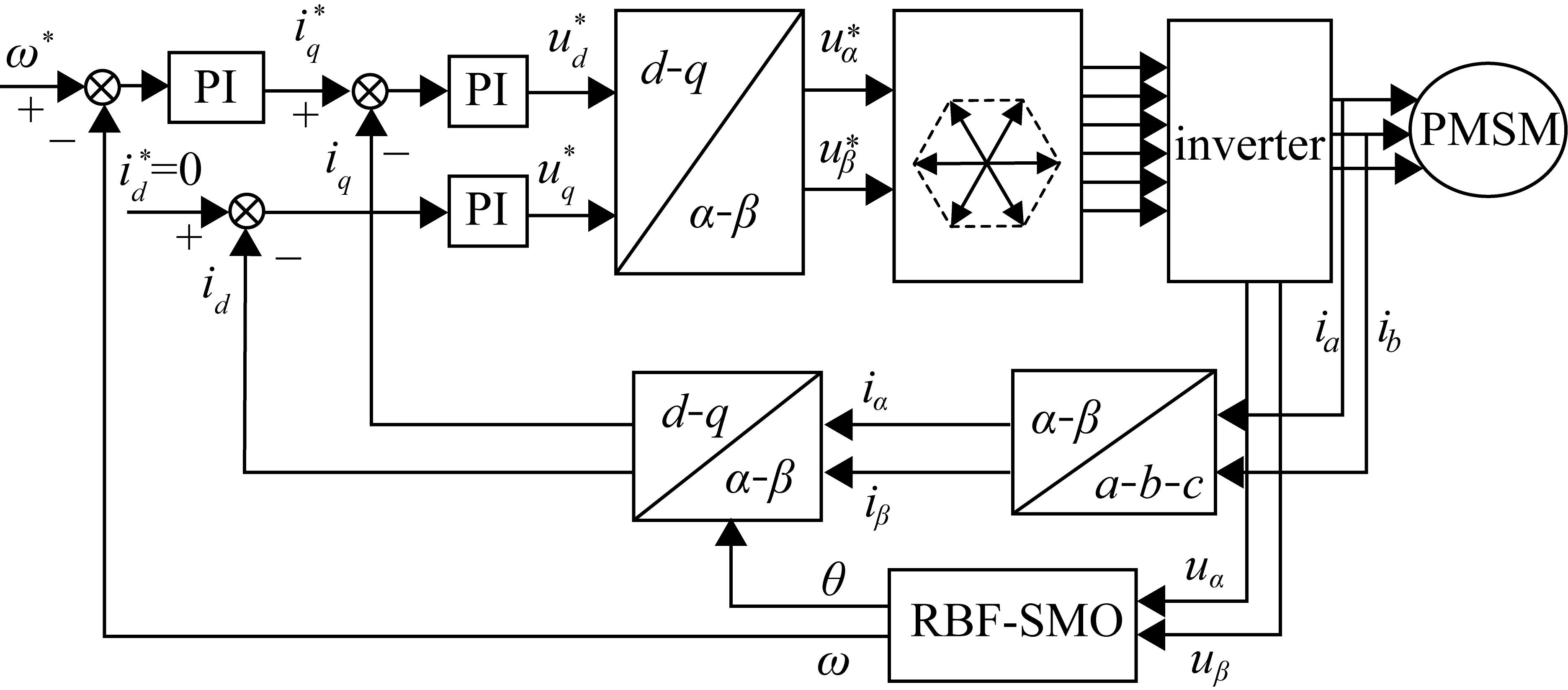
圖4 Simulink仿真結構框圖

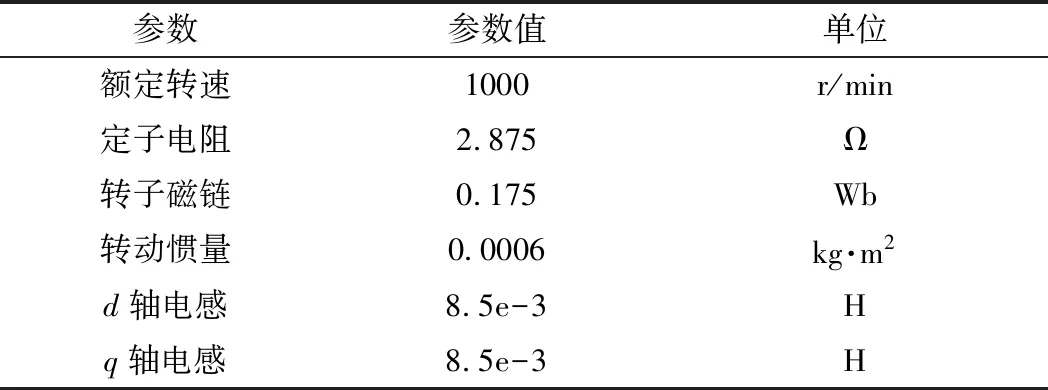
參數參數值單位額定轉速1000r/min定子電阻2.875Ω轉子磁鏈0.175Wb轉動慣量0.0006kg·m2d軸電感8.5e-3Hq軸電感8.5e-3H

仿真模型中速度環調節器PI參數為Kp=1,Ki=0.2,兩個電流環PI參數都為Kp=17,Ki=5750。電機設定轉速為1000 r/min。

仿真實驗將把本文的RBF網絡-滑模觀測器方法和傳統滑模觀測器方法(分別簡寫為SMO和RBF-SMO)對于電機相關參數的估計值分別與電機參數實際值進行對比。在整個永磁同步電機的控制系統中，由于模塊間不可避免的耦合關系，SMO和RBF-SMO的輸出都將通過影響電機的實際運行參數間接地影響兩個模塊各自的輸入，而所提出方法的有效性可以通過整個系統的運行性能來驗證。因此參照圖4所示仿真框圖中RBF-SMO模塊的輸入和輸出，以下對于仿真結果的分析討論將重點展示輸入的反電動勢和輸出的位置及速度估計。其中，為方便觀察，反電動勢和角度單位均采用標準化處理，其中角度映射范圍為(0,2π)。

兩種方法估計的α軸、β軸反電動勢及其局部放大圖分別如圖5和圖6所示。

圖5和圖6為SMO方法和RBF-SMO方法對于電機反電動勢(α軸和β軸)的估計對比圖。從圖中可以看出，利用神經網絡的學習和逼近能力，所提出的方法有效減弱了滑模觀測器的抖振，使得估計的反電動勢抖動更小，更接近真實值。同時，準確的反電動勢估計值也將使速度跟蹤更精確。

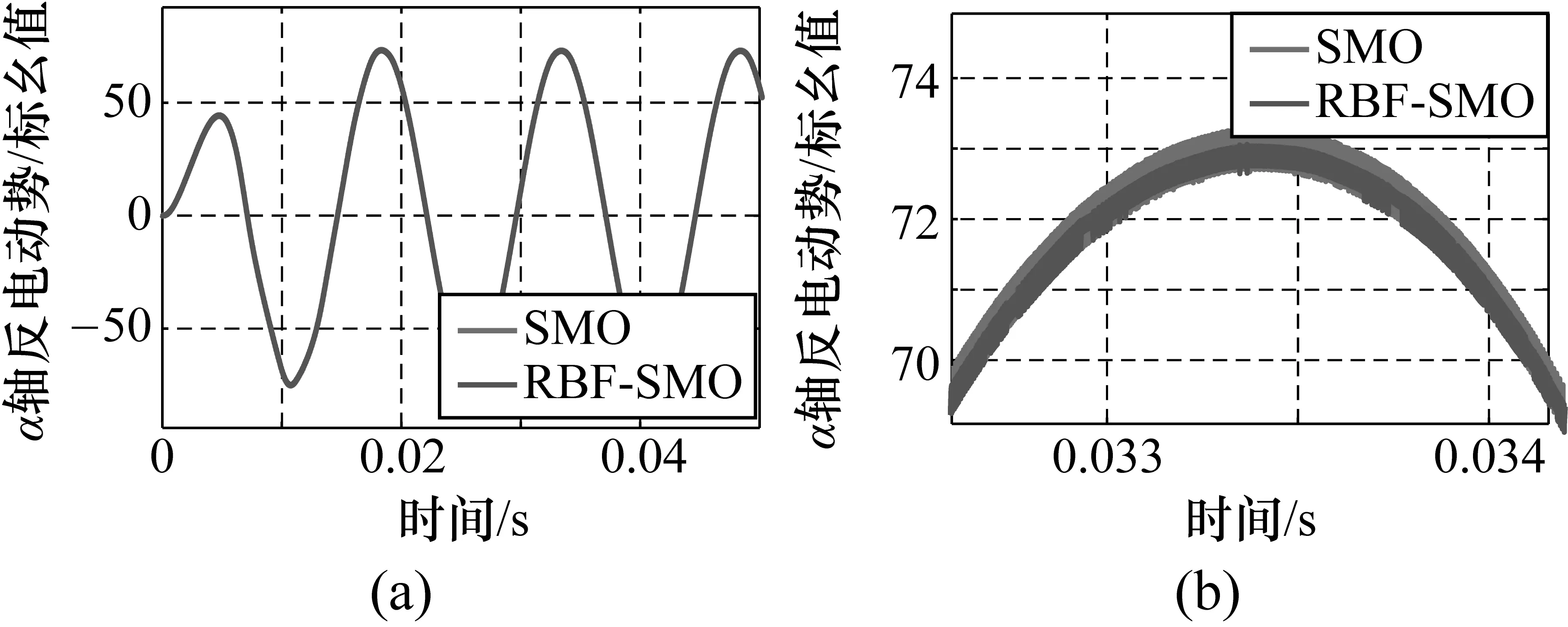
圖5 估計反電動勢vα及其局部放大圖

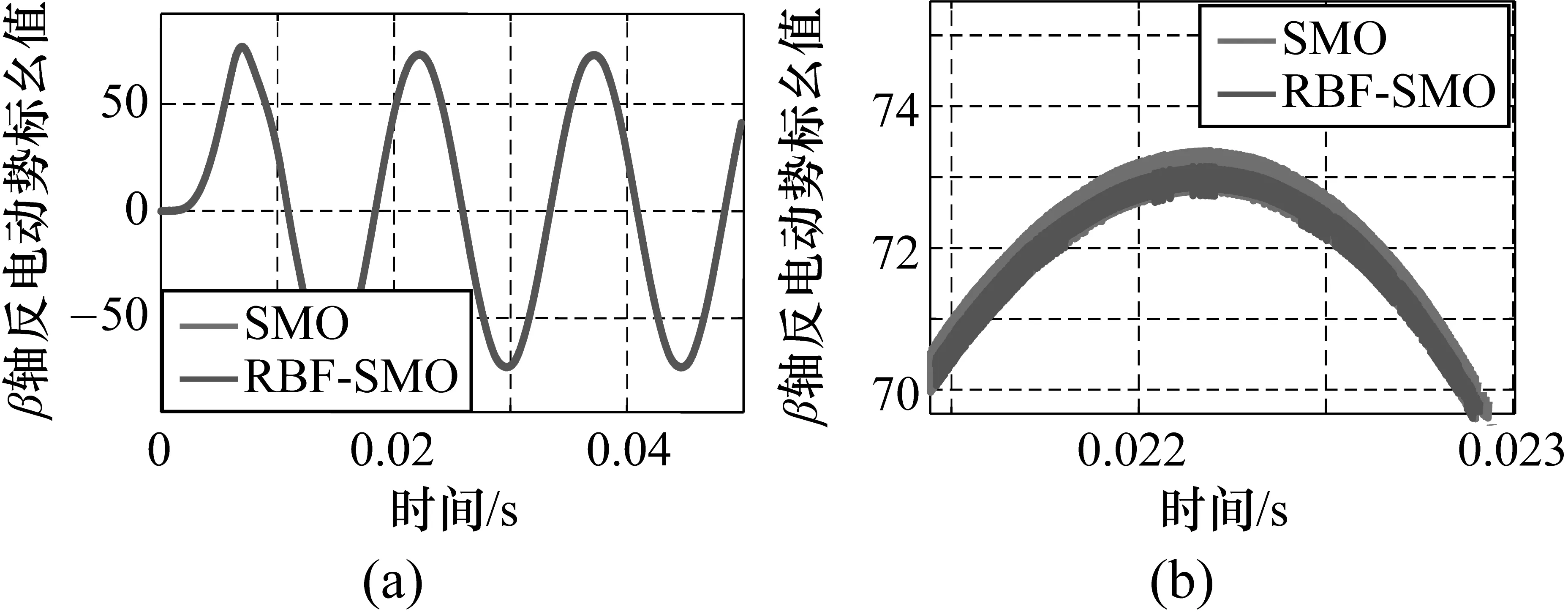
圖6 估計反電動勢beta及其局部放大圖

兩種方法對轉子位置及速度的估計及其局部圖分別如圖7和圖8所示。

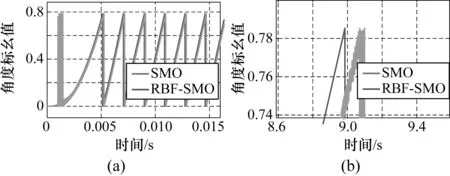
圖7 轉子估計位置及其局部放大圖

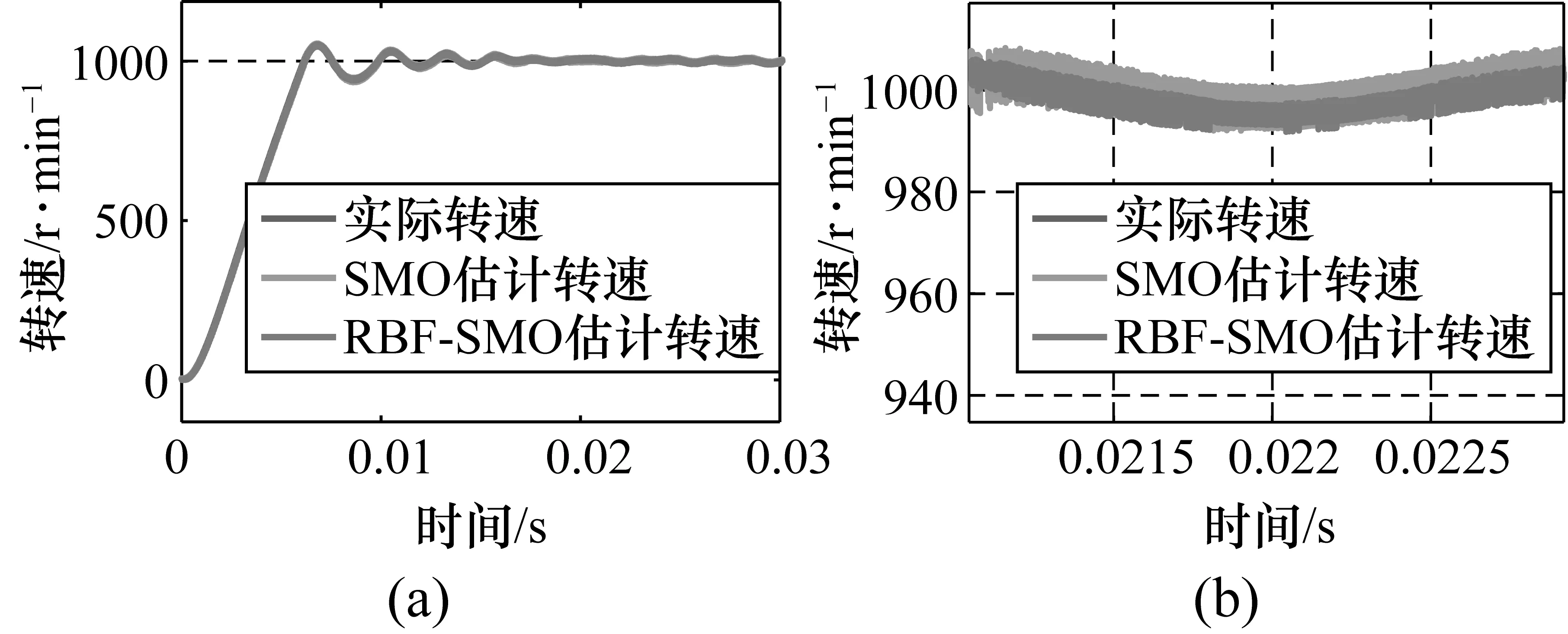
圖8 估計轉速及其局部放大圖

圖7(b)為傳統SMO方法和RBF-SMO方法對轉子位置估計的對比圖。從圖中可以看到，RBF-SMO方法對于轉子位置的估計與轉子實際位置之間的誤差相對傳統SMO方法更小，提供的位置信息更精確。如前所述，這樣的效果當是由對反電動勢更加精確的估計所致。精確的位置估計必然帶來更精確的速度估計，進而如圖8(b)所示，基于所提出的RBF-SMO方法所提供的轉子速度相對于傳統SMO方法抖動較小，最終使得電機的運轉更加平穩。

5 結束語

本文針對永磁同步電機提出一種使用RBF神經網絡調節滑模觀測器增益的無傳感器位置辨識方法，并對其估計效果進行了分析；其中，通過Lyapunov穩定性理論對該控制器的穩定性進行了證明。仿真結果表明，所提出的方法能夠有效減弱傳統滑模方法中的抖振問題，進而提供更準確的轉子位置信息，增強系統魯棒性。實驗結果更進一步印證，該方法可經適當簡化應用于實踐。