高中數學智慧課堂教學思考

摘 要：在高中數學教學中，構建智慧課堂，主要是為了促進學生智慧發展，完善學生人格。而教師作為智慧課堂構建的引導者，需要將自身的教育智慧完全發揮出來，并能夠在教與學的活動之中關注學生的發展，幫助其提升思維品質，這樣才能形成充滿活力、和諧的課堂教學狀態。

關鍵詞：高中數學;數學教學;智慧課堂

成尚榮教授通過對有關“智慧”研究的論述進行綜合分析之后提出：智慧，其本身屬于一種整體品質，主要是在情境之中誕生與表現，基于能力作為基本核心，以美德與創造作為方向，將頓悟和敏感作為特征，以機智來作為表現，人文素養與科學素養的相互結合，就賦予其張力和底蘊。教師作為智慧課堂構建的引導者，需要將自身的教育智慧完全發揮出來，能夠在實際教與學的活動中關注學生的發展，幫助學生提升思維品質，從而營造一種充滿活力、和諧的課堂教學氛圍。在高中數學的智慧課堂中，構建藝術，就是基于“互聯網+”和現代的教學媒體，并充分利用教師的課堂智慧，提高數學課堂的教學效率，促進學生更好的發展。

一、智慧課堂分析

所謂智慧，實際上就是“彰顯聰敏、謀略豐富、見解獨到”。“智慧課堂”主要是在實際的教學環節生成對應的學習智慧，并且還能提高教學的質量和效率。針對知識課堂來說，高中數學智慧課堂就是從原本的知識課堂逐漸朝著智慧課堂轉移，這樣才可以推動數學學習的智慧發展，基于智慧課堂的有效應用，將傳統課堂的弊端打破，最終實現高質量、高效率的學習[1]。

二、高中數學智慧課堂教學幾點思考

雖然利用信息技術教學手段，已經使教學質量和效率得到了很大提升，學生也越來越喜歡這種教學模式，但要想發揮智慧課堂更大的作用，每位數學教師都需要在課前、課中、課后投入更多的心思。它無形當中，又對教師提出了更高的要求。每位教師不僅要制作適合自己教學風格的課件，合理利用信息技術手段，還要充分利用自己的教學智慧讓學生快樂學習、發展能力。對于當前智慧課堂的數學教學，我認為并不是完全摒棄傳統教學方法，也不全應用信息技術，而是有效結合兩者。在當前的高中數學智慧課堂教學中，為了滿足課堂教學的需求，我們在教學方法上做些嘗試，比如運用問題導學、合理利用智慧課堂、利用思維導圖、運用留白自我提煉幾個層次進行改進，從而滿足新課改對數學教學的要求，促進學生的發展。

（一）運用問題導學，激發學生思維細胞

所謂問題導學法，就是基于課堂之前所設計的一系列問題，利用問題將整個課堂直接串聯起來，確保在問題回答中，學生可以保持高度集中，最終掌握知識。

例如，以“立體幾何初步”中的“空間幾何體”知識作為案例。通過設計，制定如下問題：棱柱包含哪幾種？每一種定義、圖形和性質是怎樣的？正棱錐需要滿足哪些條件？等等。對于這一部分教師提出的問題，也可以讓學生大膽提出自己的想法，對于問題進行后續的追問。如“在一個幾何體中，當提及一定的時候，其球表面積是否最小”這一問題，雖然這一個問題的結果是“是”，但是學生所思考的是利用反向思維，然后追問：當表面積一定，那么其球的體積是否最大。這一種追問和被追問的模式，就可以讓整個課堂真正“活”起來，并且表現出較好的氛圍。利用問題導學模式，就可以提升智慧課堂教學效率，其主要通過問題來幫助學生集中注意力，同時在實際的回答之中，針對相對模糊的部分答案，也可以選擇利用假設、求證等一系列的方式來回答，其本身也算是對智慧的引導，同時，就邏輯思維能力而言，也是一種非常好的磨煉方式。

（二）合理利用平板電腦，構建智慧課堂

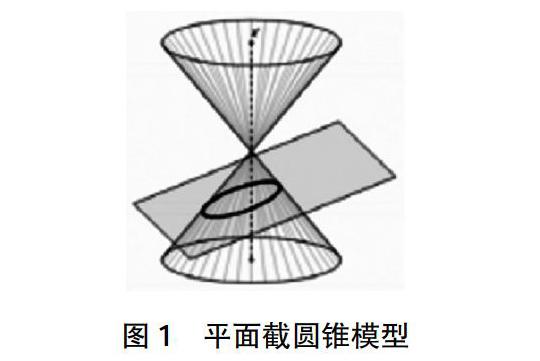
高中數學之中對于教師產生困擾的是學生“立體感”不強，甚至是毫無立體感，對于立體幾何學生是茫然不知所措。但是擁有平板電腦，就可以讓立體幾何真正“活”起來，通過旋轉，合理利用3D模型的演示，就可以呈現立體感，并且幫助學生建立對應的空間感。一直以來，在高中數學中，“圓錐曲線與方程”是難點，但是也是高考的重點，在這一節課，要讓學生對一個平面截一個圓錐面加以體會，由于不同位置平面獲取不同的圖形，從而初步認識橢圓、拋物線、雙曲線，是立體幾何與平面幾何的過渡。在實際的教學環節，教師就可以將平板電腦的優勢發揮出來，為學生呈現好的動畫模擬，最終通過改變位置加以觀察（如圖1）。

教師：通過自己的觀察，大家是否發現改變平面位置時候，截面的圖形是否存在不一樣，是否可以進行概括？

學生：在改變平面位置之后，有橢圓、圓，也就拋物線和雙曲線。

教師：如果我們假設主線和軸線之間的夾角為θ，而軸線同平面之中的正投影夾角為α，我們可以了解當θ與α的大小關系變化時，其實際的截面圖形變化（圖2）。

（三）利用思維導圖，提高知識邏輯條理

數學本身是一門具有條理性和邏輯性的學科，但是數學知識中的很多概念，對于部分公式或者是定理，教材之中往往就會利用一定篇幅的文字來加以說明，為了避免因為閱讀文字而分散自己的注意力，就可以選擇利用思維導圖的方式來提升知識的邏輯條理性，最終打造智慧課堂[2]。

如針對“復數”的學習中，在講課之前，首先就可以利用思維導圖的方式，讓學生清晰地了解這一章節的內容，如圖3所示。

復數復數的基本性質復數的分類復數的向量表示共軛復數復數的代數運算代數形式的各種運算i的性質復數域上因式分解復數的三角運算三角形式的各種運算復數的模與性質復數的輻角與性質復數與幾何復數計算的幾何意義復數與解析幾何

這一張思維導圖實現了整個單元與章節內容的合理梳理，在正式上課之前，教師首先展示出思維導圖，主要是讓學生對教師這一章節的內容了然于心，從而真正掌握需要掌握的學習任務。其次，隨著教學內容的持續深入，在自行補充之下，學生也可以將其完善，這樣就可以基于學生實際理解度和對知識進行分析，從而形成一張專屬于自己的思維導圖（見圖4所示）。當對復數相關的內容有了完整性的學習之后，所有的知識點都可以利用思維導圖的方式加以呈現，這就是一種將書本讀薄的有效模式，無論是學生現在的學習，還是對于經過一段時間的復習，都可以不用再回到教材之中進行一頁一頁的翻、一點一點的找，而是利用這一張思維導圖，可以實現知識的擴散與聯想，很明顯，這一種方式是非常高效的。

（四）自我提煉，用留白來完善小結

良好的開端還需要好的結尾，教師在課堂小結的時候適當進行“留白”，需要將學生的自主性充分發揮出來，讓學生可以實現自我鍛煉，能夠真正帶著問題走出課堂，進而在有限之中尋求無限。

例如，以函數y=Asin（ωx+φ）的圖象為例，教師就可以要求學生對本節課所學習的知識加以回顧，然后歸納出y=sinx圖象變換成為y=Asin（ωx+φ）圖象的基本步驟，并且嘗試著將圖5的流程圖完成，提煉出“先平移后伸縮”“先伸縮后平移”兩種不同的變換方式，這樣有利于智慧課堂的合理構建[4]。

總而言之，對于高中數學教學而言，合理構建智慧課堂，才是當前高中數學教學中需要重點解決的問題。因此，高中數學教師需要懂得合理的創設、引領以及捕捉，這樣才能在學習過程中讓學生充滿激情，才能讓數學課堂充滿智慧與活力。

參考文獻：

[1]劉邦奇，李新義，袁婷婷，董晶晶.基于智慧課堂的學科教學模式創新與應用研究[J].電化教育研究，2019（4）：1-6.

[2]朱建國.基于高中數學核心素養的智慧課堂教學研究：《瞬時變化率》一課的教學設計與思考[J].數學之友，2018（2）：42-43.

[3]薛超群.智慧課堂教學模式研究[J].寧德師范學院學報（自然科學版），2018（1）：101-103.

[4]安永新.高中數學教學實踐創新探究[J].學周刊，2016（23）：161-162.

作者簡介：彭曉芹（1982.12—），女，籍貫：安徽六安，民族：漢，學歷：職稱（職務）：中學二級，研究方向：應用數學。