超音速分離線噴管內流場數(shù)值模擬①

李 鑫，李 耿，王周成，張 飛，趙 康，劉元敏

(中國航天科技集團有限公司四院四十一所，西安 710025)

0 引言

超音速分離線噴管(Supersonic Splitline Nozzle)是固定部分與可動部分之間的分界線位于噴管超音速區(qū)域的一種矢量噴管[1]。相比亞音速分離線噴管，具有零部件數(shù)量少、結構簡單、偏轉效率高以及能夠減小發(fā)動機后開口尺寸等一系列優(yōu)點，歐美等發(fā)達國家在這一領域開展了較系統(tǒng)的研究，并在多發(fā)戰(zhàn)術發(fā)動機和大型發(fā)動機上進行了熱試車[2-6]。

本文通過流場仿真，給出了超音速分離線噴管不同擺角下的內流場分布規(guī)律，獲得了噴管的受力情況，對比分析了超音速分離線與亞音速分離線噴管的偏轉效率，并給出了擺動對噴管內兩相流粒子濃度分布的影響，為噴管設計及工程研制提供理論參考。

1 數(shù)學與物理模型

圖1給出了超音速分離線與亞音速分離線噴管(Subsonic Splitline Nozzle)的擺動對比示意圖。可看出，亞音速分離線噴管在擺動過程中噴管內型面保持不變，內流場基本不受干擾；而超音速分離線噴管的擺動使得內型面發(fā)生了較明顯的變化，內流場出現(xiàn)了復雜的壓縮-膨脹波系[7]，流場不再具備軸對稱的特點，從而可能會對噴管的氣動力及燒蝕情況造成影響。

1.1 基本假設

固體火箭發(fā)動機內流場的流動屬于典型的二相流動過程，這里采用Euler-Lagrangian法對該過程進行數(shù)值模擬。在Euler坐標系中求解氣相控制方程，同時在Lagrangian坐標系中對凝相顆粒進行跟蹤，兩者之間的耦合通過在控制方程增加源項來完成。

在進行數(shù)值計算時，對內流場的流動做如下假設：

(1)不考慮燃氣中的化學反應；

(2)不考慮凝相的燃燒、蒸發(fā)、破碎過程；

(3)假設過程為定常流動。

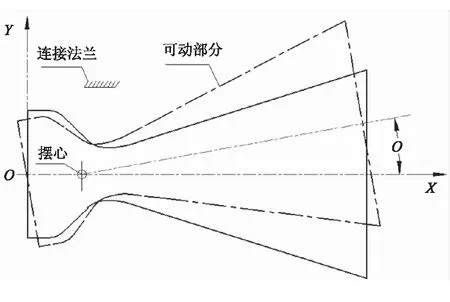
(a)亞音速分離線噴管

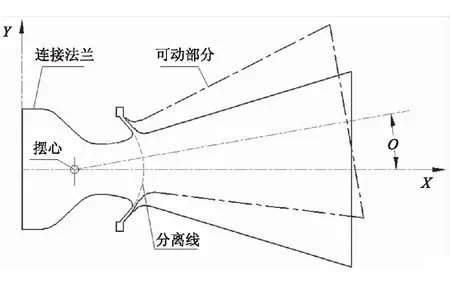
(b)超音速分離線噴管

1.2 氣相控制方程

氣相質量守恒方程：

(1)

氣相動量守恒方程：

(2)

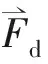
考慮凝相的作用，氣相的能量守恒方程為

(3)

式中I為比內能；Qd為顆粒作用的能量源相；σ為熱通量項，包括熱傳導項和焓擴散項。

1.3 兩相流模型

兩相流模型采用DDM(Discret Droplet Model )模型，將顆粒看成離散質點，顆粒的運動方程為

(4)

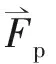
顆粒的軌跡方程為

(5)

顆粒的能量方程為

(6)

式中hp為顆粒表面對流換熱系數(shù)；Ap為顆粒表面積。

在Lagrangian坐標系下，對每個粒子進行跟蹤，計算顆粒相的質量、動量、能量與連續(xù)相的交換量成為源相，加入到隨后連續(xù)相的計算中，連續(xù)相計算又對凝相計算產(chǎn)生影響，二者交替計算，直至收斂[8-13]。

1.4 物理模型及計算域

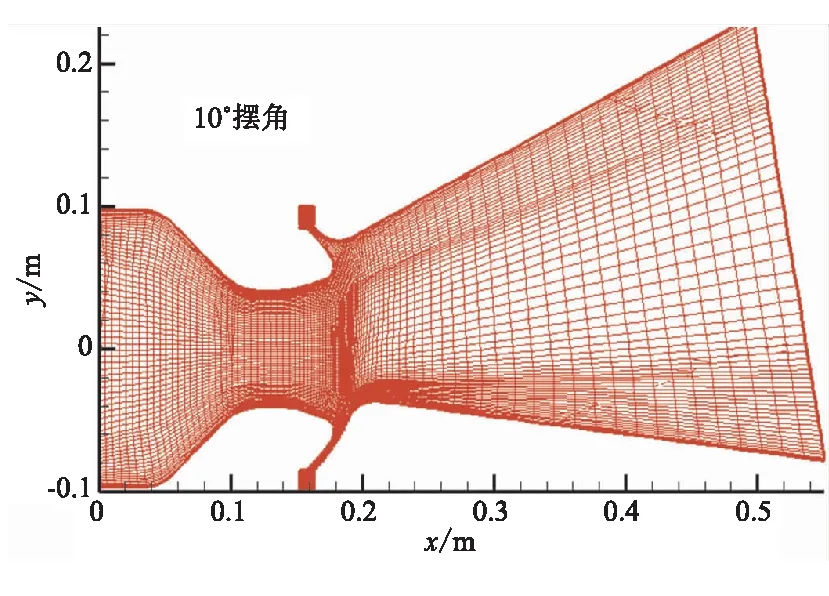
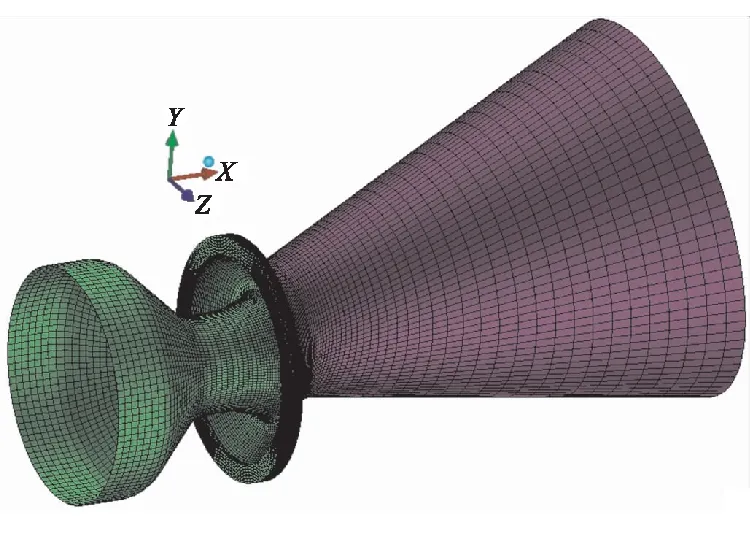
采用ICEM軟件進行六面體網(wǎng)格劃分，為保證計算結果準確，對壁面處網(wǎng)格進行加密處理，確保第一個內節(jié)點P位于對數(shù)分布律成立的范圍內。采用疏密兩種網(wǎng)格進行網(wǎng)格無關性驗證，以發(fā)動機推力作為指標。0°擺角結果表明，兩種網(wǎng)格計算得到的發(fā)動機軸向推力幾乎完全一致，側向推力相差0.075%。因此，較稀疏的網(wǎng)格完全可滿足計算要求。

圖2為超音速分離線噴管計算模型及網(wǎng)格劃分情況。噴管喉徑為φ81 mm，入口部位收斂比為5.7，出口擴張比為15.2，活動體與固定體分界線位于喉部下游，擴張比為1.7，處于超音速流場區(qū)域。擴張段型面為直錐型。為了提高精度和計算效率，采用結構網(wǎng)格離散計算區(qū)域[14-15]，網(wǎng)格數(shù)量為66.16萬。

(a)對稱面網(wǎng)格

(b)表面網(wǎng)格

2 物性參數(shù)及邊界條件

數(shù)值計算采用FLUENT 軟件。燃氣的定壓比熱容和氣體常數(shù)根據(jù)熱力計算結果獲得，燃氣密度按照理想氣體狀態(tài)方程給定，粘性系數(shù)按照Sutherland公式計算，熱導率選擇kinetic-theory。因標準κ-ε湍流模型用于強旋流或者帶有彎曲的壁面流動時會出現(xiàn)一定失真，這里選用RNGκ-ε模型提高數(shù)值計算的準確度。氣相壓力入口邊界為入口壓強10 MPa，總溫3781 K。氣相壓力出口邊界為出口壓強101 325 Pa，出口環(huán)境溫度293 K。氣相壁面邊界條件采用無滑移及絕熱壁面邊界條件；假定凝相粒子的直徑遵循Rosin-Rammler分布，平均粒徑為4×10-5m，粒徑范圍為1×10-5～4×10-5m，凝相粒子的初始速度為0.1 m/s，壓力入口及出口均采用逃逸邊界，壁面采用反彈模型[16]。

3 計算結果與分析

相比亞音速噴管，超音速分離線噴管的擺動會對噴管內流場分布及噴管的氣動力產(chǎn)生更大的影響。因此，本文以噴管擺角作為主要變量，對0°、2.5°、5.0°、7.5°、10.0°不同擺角下的內流場進行計算分析。

3.1 不同擺角對馬赫數(shù)分布云圖的影響

圖3～圖5給出了超音速分離線噴管0°、5.0°、10.0°三個典型擺角下擺動平面內內流場馬赫數(shù)分布云圖及分離線位置狹縫區(qū)域環(huán)向剖面的速度和流線分布圖。從圖3可看出，0°擺角下噴管內流場呈軸對稱分布，噴管入口燃氣經(jīng)過收斂段加速之后在喉部達到音速，之后經(jīng)擴張段進一步加速為超音速氣流；燃氣在噴管活動體小端部位產(chǎn)生了一系列錐形壓縮波，此族壓縮波沒有在軸線附近封閉，在軸線附近還有一系列膨脹波，引導超音速氣流繼續(xù)加速直到噴管出口。0°擺角下分離線狹縫區(qū)域流速很低，最高速度僅為23.2 m/s，且區(qū)域內為不規(guī)則的漩渦流動。

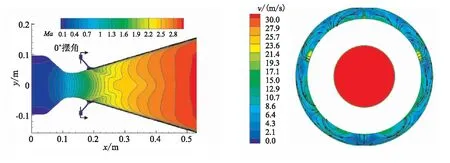
(a)馬赫數(shù)分布云圖 (b)速度流線圖

圖4為5.0°擺角下噴管擺動平面內的馬赫數(shù)云圖及分離線狹縫區(qū)域環(huán)向剖面速度云圖和流線圖。從馬赫數(shù)分布圖可看出，相比0°擺角，超音速氣流在噴管活動體小端的壓縮波已增強為斜激波，而且噴管內流場已不再具有軸對稱的特性。在噴管擺動平面內，活動體小端靠近軸線一側的激波強度最強，而遠離軸線一側的激波強度則較弱。

從環(huán)向剖面的速度和流線圖可看出，5.0°擺角下狹縫區(qū)域已經(jīng)存在明顯的由“滯止區(qū)”向“源區(qū)”的環(huán)向流動，部分區(qū)域的速度已經(jīng)達到834.0 m/s。從馬赫數(shù)云圖可注意到，在“源區(qū)”與噴管擴張段相交的地方有一簇不規(guī)則曲面激波。這是因為“源區(qū)”附近狹縫區(qū)域的超音速氣流必須經(jīng)過激波的壓縮以滿足邊界條件，然后再經(jīng)過擴張段的擴張作用，加速達到超音速。

圖5為10.0°擺角下噴管擺動平面內的馬赫數(shù)云圖及分離線狹縫區(qū)域環(huán)向剖面速度和流線圖。從馬赫數(shù)分布云圖可看出，隨著擺角的增大，噴管活動體小端產(chǎn)生的激波均進一步增強。其中，靠近軸線一側活動體激波強度的增幅最大。

從環(huán)向剖面的速度和流線圖可看出，10.0°擺角下狹縫區(qū)域的環(huán)向流動進一步加強，部分區(qū)域的速度已經(jīng)達到1031.9 m/s。從馬赫數(shù)云圖可注意到，在“源區(qū)”與噴管擴張段相交地方的曲面激波也進一步增強。

(a)馬赫數(shù)分布云圖 (b)速度流線圖

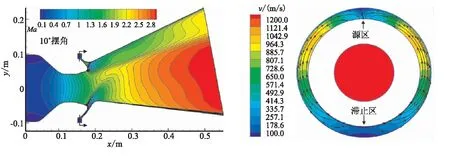
(a)馬赫數(shù)分布云圖 (b)速度流線圖

3.2 不同擺角對壓力分布云圖的影響

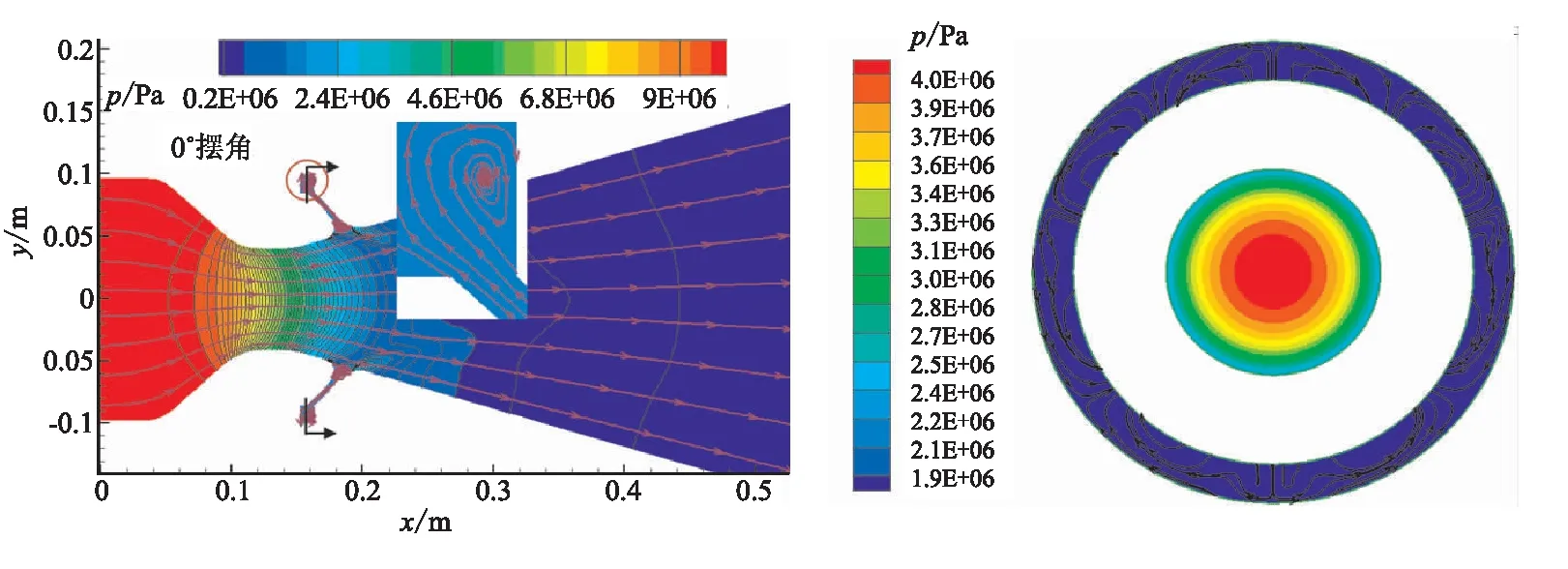
圖6～圖8給出了超音速分離線噴管0°、5.0°和10.0°三個典型擺角下擺動平面內壓力云圖及分離線狹縫區(qū)域環(huán)向剖面的壓力云圖和流線分布圖。從圖6可看出，0°擺角下噴管內壓力呈軸對稱分布，由于活動體小端區(qū)域壓縮波的存在，致使波后壓強有小幅的增加。從分離線狹縫區(qū)的局部放大圖可看出，0°擺角下區(qū)域內存在不規(guī)則漩渦流動。

從環(huán)向壓力和流線圖可看出，此時狹縫區(qū)內壓強幾乎處處相等，約為1.78 MPa，為流動滯止區(qū)，這與圖3中速度分布趨勢也相吻合。燃氣在此區(qū)域速度很低，呈現(xiàn)不規(guī)則流動狀態(tài)。

從圖7可看出， 5.0°擺角下噴管內的壓力分布已不具有軸對稱的特征。由于活動體小端激波的存在，該區(qū)域壓強進一步升高。在噴管擺動平面內，靠近軸線一側的活動體小端的壓強升高更加明顯，遠離軸線一側的升高幅度則較小一些。另外，從分離線區(qū)域的局部放大圖可看出，5.0°擺角下狹縫區(qū)域內的漩渦流動消失，轉變?yōu)椤霸磪^(qū)”，源區(qū)內的壓強較0°擺角下顯著增大，達到2.81 MPa。

從環(huán)向剖面的壓強和流線圖可看出，5.0°擺角下分離線狹縫區(qū)域已經(jīng)存在明顯的環(huán)向壓強差，“滯止區(qū)”即靠近噴管軸線的一側壓強最高，達到3.17 MPa，而遠離軸線一側的“源區(qū)”壓強則較低，從而導致區(qū)域內形成了由“滯止區(qū)”向“源區(qū)”的環(huán)向流動。

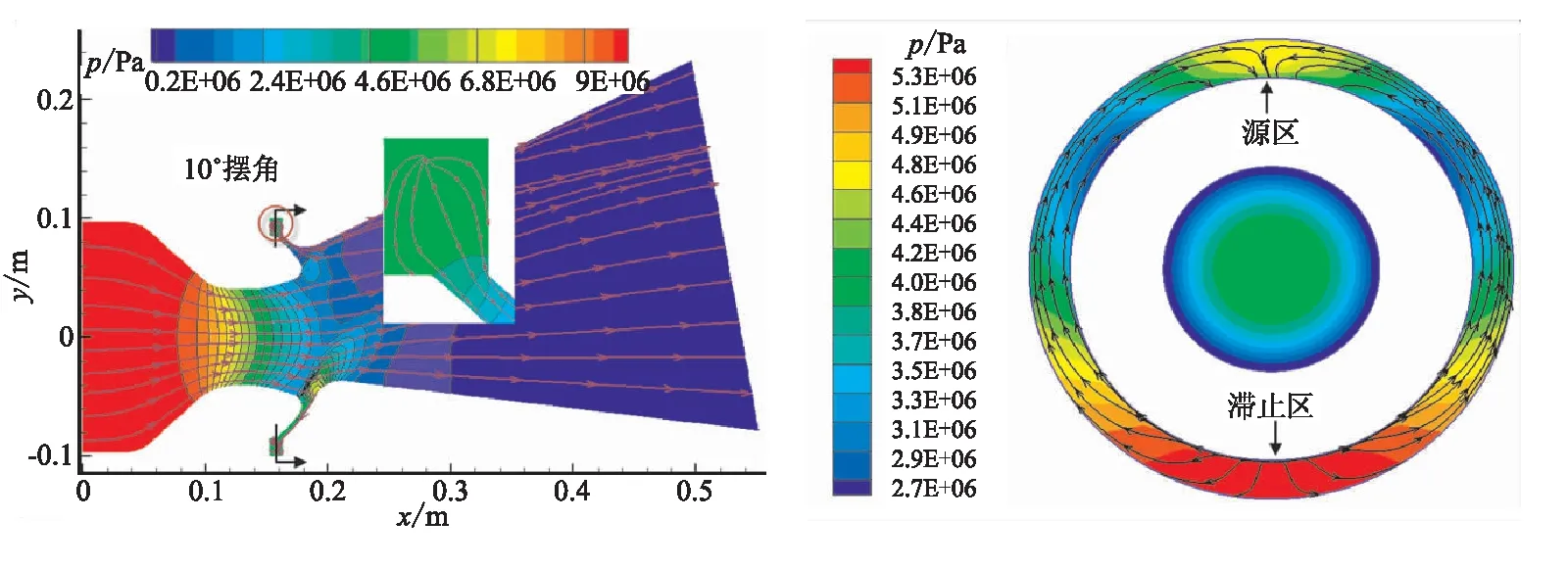
從圖8可看出，隨著擺角的增大，噴管內壓力場的非對稱性進一步加強，活動體小端的壓強也進一步增大。其中，靠近軸線一側的壓強增幅最大。從分離線區(qū)域的局部放大圖可看出，10.0°擺角下狹縫區(qū)域內流動狀態(tài)仍為“源區(qū)”，壓強達到4.73 MPa。

從環(huán)向剖面的壓強和流線圖可看出，10.0°擺角下分離線狹縫區(qū)域環(huán)向壓差進一步加大，“滯止區(qū)”即靠近噴管軸線的一側壓強最高，達到5.48 MPa，比“源區(qū)”高出2.76 MPa，這也致使區(qū)域內由“滯止區(qū)”向“源區(qū)”的環(huán)向流動進一步增強，流動速度增大。

(a)壓力分布云圖 (b)環(huán)向流線圖

(a)壓力分布云圖 (b)環(huán)向流線圖

(a)壓力分布云圖 (b)環(huán)向流線圖

3.3 噴管受力及放大因子分析

從上述分析可知，擺動會引起超音速分離線噴管內流場的顯著變化，從而導致噴管內的氣動力分布改變，影響發(fā)動機的推力大小及方向。這里對不同擺角下超音速分離線噴管內流場進行壓力積分，獲得不同方向的受力情況，如表1所示。表1中，同時給出了亞音速分離線噴管對應擺角的受力情況。從表1可看出，在擺動角度相同的條件下，超音速分離線噴管的軸向力(X向)略小于亞音速分離線噴管，而徑向力(Y向)則顯著大于亞音速分離線噴管。這說明在擺動條件下，相比亞音速分離線噴管，超音速分離線噴管的軸向力略有損失，而徑向力則有較明顯的增大，即噴管的偏轉效率會顯著提高。從流場計算結果分析可知，造成上述現(xiàn)象的主要原因是超音速分離線噴管在擺動后引起了擴張段上非對稱的壓縮-膨脹波系，該波系導致氣流進一步向著噴管的擺動方向發(fā)生了偏轉，引起了徑向力的增大，而在軸向上的分力則會相應減小。另外，超音速分離線噴管擺動引起的壓縮-膨脹波系造成的流動損失，也是導致噴管軸向推力減小的原因。

由于徑向力對飛行器的偏轉起著主要作用，為便于研究，定義相同機械擺角下超音速分離線噴管和亞音速分離線噴管的徑向力比值為噴管的偏轉放大因子。圖9和10分別給出了超音速分離線噴管軸向推力比值及偏轉放大因子與擺角的關系。可知，隨著擺角增大，超音速分離線噴管軸向力損失增大；而偏轉放大因子則隨著擺角增大呈現(xiàn)先增大、后減小的變化規(guī)律，但其值始終大于1.0，從本文算例來看，2.5°擺角時偏轉放大達到最大，其值為1.36。

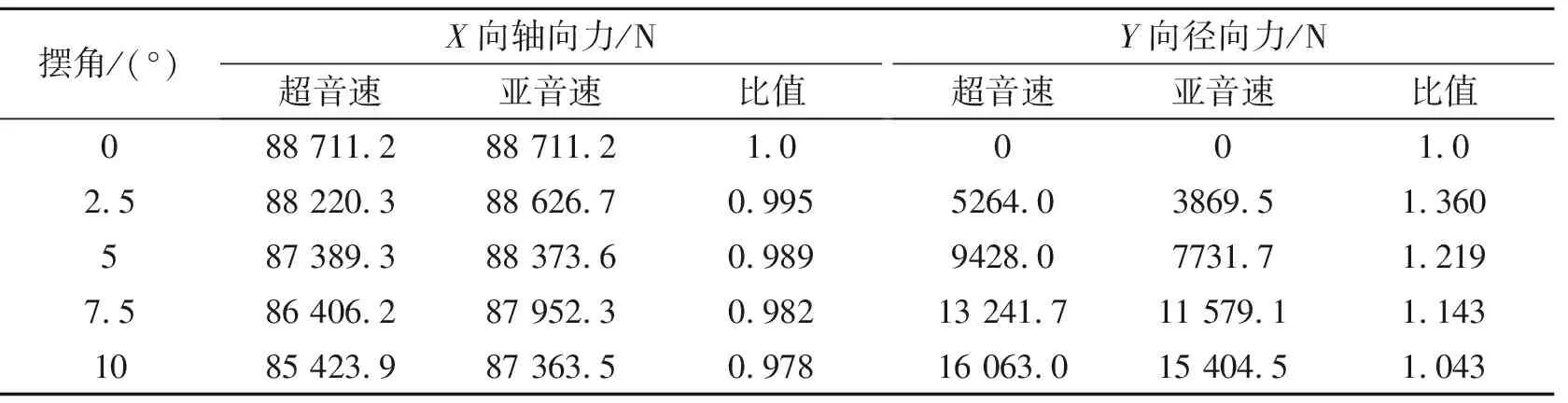
表1 噴管作用力隨擺角變化情況對比

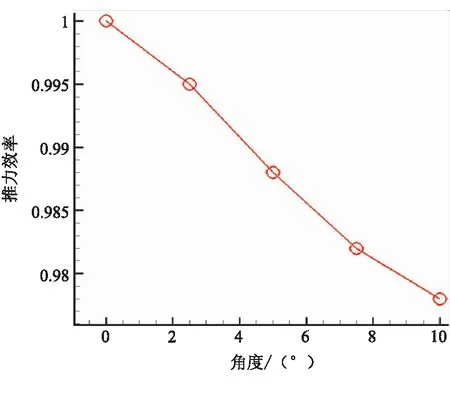
圖9 軸向推力效率

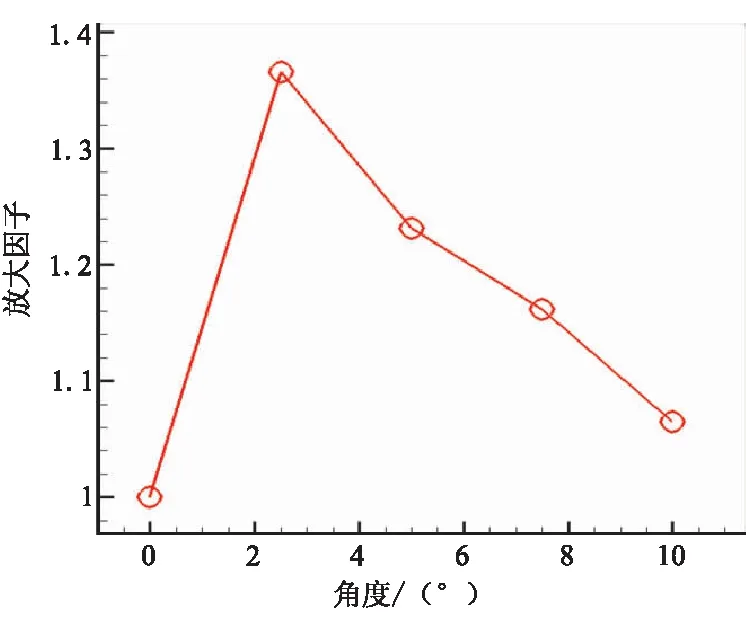
圖10 偏轉放大因子

3.4 噴管偏轉對粒子分布規(guī)律的影響

圖11～圖13給出了0°、5.0°、10.0°三個典型擺角下超音速分離線噴管內流場粒子濃度的分布情況。可看出，0°擺角下，Al2O3粒子基本集中在軸線附近，呈現(xiàn)對稱分布，整個噴管喉部下游內壁面基本沒有粒子的撞擊，極限流線與壁面之間形成“無粒子區(qū)”[17]。5.0°擺角下，噴管活動體小端一側由于擺動靠近流場的粒子集中區(qū)，在氣相流場的共同作用下，Al2O3粒子的分布不再具有軸對稱特性，靠近軸線一側的活動體小端粒子濃度顯著增大。當擺角達到10.0°時， Al2O3粒子分布的非對稱特性進一步加劇，噴管活動體小端靠近軸線一側受到粒子撞擊，致使該區(qū)域粒子濃度進一步增加。

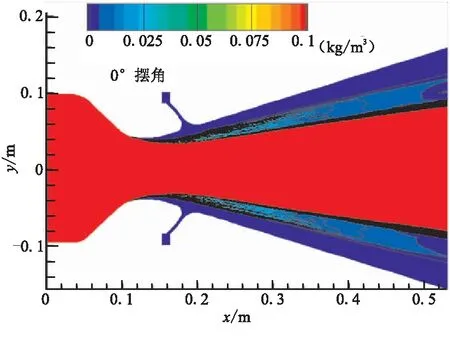
圖11 粒子濃度分布(0°)

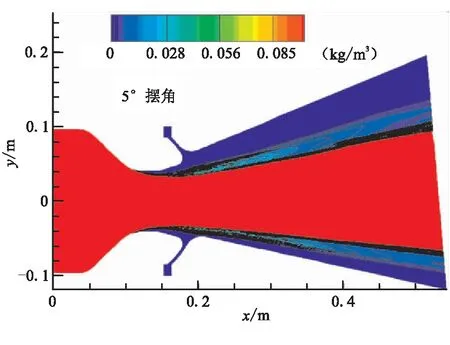
圖12 粒子濃度分布(5.0°)

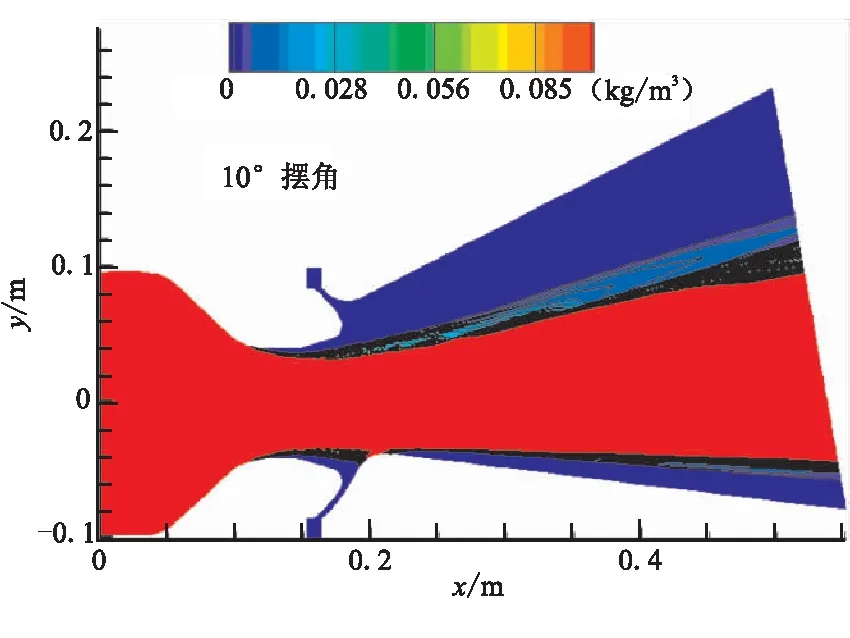
圖13 粒子濃度分布(10.0°)

4 結論

(1)從計算結果可知，與亞音速分離線噴管不同，擺動條件下超音速分離線噴管內流場呈現(xiàn)顯著的三維流動特征，且隨著擺角增大，噴管內激波強度和內流場的非對稱性不斷增加。

(2)在相同擺角下，相比亞音速分離線噴管，超音速分離線噴管的軸向分力略有減小，而徑向分力則呈現(xiàn)增大的趨勢；超音速分離線噴管與亞音速分離線噴管的徑向分力比值，即偏轉放大因子，則隨噴管擺角呈現(xiàn)先增大、后減小的變化規(guī)律，但其值始終大于1.0，本算例中的最佳放大因子為1.36，對應的噴管擺角為2.5°。

(3)隨著擺角增大，超音速分離線噴管內流場Al2O3粒子分布的非對稱性逐漸加強，噴管活動體小端的粒子濃度也逐漸增大，由此可能造成的燒蝕增大在超音速分離線噴管的熱防護設計中應予以考慮。