非均勻剛度彈性邊界結構優化設計及實驗驗證①
杜凱繁,郝 鵬,董曼紅,王 博
(1. 大連理工大學 工業裝備結構分析國家重點實驗室 工程力學系,大連 116023;2. 北京宇航系統工程研究所,北京 100076)
0 引言
運載火箭地面實驗加載系統通常采用均勻剛度的彈性邊界將軸壓彎矩等載荷加載至主承力筒殼結構中。然而,主承力筒殼結構在真實服役狀態下載荷邊界通常是剛度非均勻的。同一載荷作用下,非均勻剛度彈性邊界使得主承力筒殼結構受到非均勻載荷作用,局部載荷較大,而傳統的均勻剛度彈性邊界使得主承力筒殼結構受到均勻載荷作用,局部載荷較小。因此,傳統的均勻剛度彈性邊界過低地估計了實驗載荷,需要提出一種非均勻剛度彈性邊界的結構設計。
面向運載火箭主承力筒殼結構,國內外學者開展大量關于筒殼軸壓實驗研究[1-6]。王博等[7-8]面向運載火箭主承力筒殼結構開展軸壓屈曲實驗,驗證實驗系統的可靠性和數值預測方法的準確性。Bisagni[9]針對筒殼結構軸壓失穩實驗開展加載方式研究,定量地分析了靜態加載與動態加載對軸壓筒殼結構的影響程度,該研究對數值仿真具有指導意義。王棟[10]通過研究彈性邊界試驗方法,即對待測結構施加彈性支撐,在分別獲得整體與支撐結構頻響后,通過頻域子結構解耦方法,去除支撐結構對待測結構的影響,以得到待測結構自由狀態頻響,進而解決自由懸吊方法進行結構自由狀態頻響測試難以滿足要求的難題。
對于航天領域主承力筒殼結構,國內外學者開展大量優化設計工作[11-20]。郝鵬等[21]針對箭體中典型的網格加筋柱殼結構,提出自適應代理模型優化設計方法,顯著提升優化設計效率。王博和郝鵬等[22]提出了針對多級加筋殼的自適應等效策略分層次優化設計方法。該方法的基本思想是將復雜的優化設計問題分解成多個簡單的優化設計問題,從而有效降低結構優化設計維度,根本上保證了筒殼結構性能分析的準確性和優化算法的穩定性。針對非均勻軸壓載荷,郝鵬等[23]提出網格加筋結構的布局優化設計方法,實現了筒殼結構的同步失效,大幅提高筒殼結構承載效率。
為解決非均勻剛度彈性邊界的設計問題,本文開展如下工作:(1)剛度等效指標選取研究,通過對比真實彈性邊界與均勻剛度彈性邊界情況下主承力筒殼結構的邊界響應,獲得剛度等效指標;(2)考慮剛度等效指標的非均勻剛度彈性邊界優化設計,以剛度等效指標為設計目標,均勻剛度彈性邊界桁條分布角度為設計變量,獲得非均勻剛度彈性邊界結構設計;(3)非均勻剛度彈性邊界結構原理性實驗,通過對比真實彈性邊界與均勻剛度彈性邊界情況下主承力筒殼結構的邊界響應,驗證該優化設計方法的有效性。
1 剛度等效指標選取
為了使得真實彈性邊界的剛度與非均勻剛度彈性邊界的剛度一致,需要等效剛度指標來定量化描述兩者的剛度分布。因此,以主承力筒殼結構邊緣處的位移響應來描述兩種邊界的剛度分布情況。
為獲得等效剛度指標,對比分析真實彈性邊界與均勻剛度彈性邊界的剛度分布情況,算例設置如表1所示。算例筒殼結構的幾何參數:直徑D=500 mm,高度H=510 mm。材料屬性:鋁合金2024,T62狀態,彈性模量E=72 GPa,泊松比0.31,屈服強度363 MPa,強度極限463 MPa,密度2.8×10-9t/mm3,延伸率0.12。單元采用ABAQUS提供的S4單元(4節點全積分殼單元)。模型節點數為9120,單元數為8968;真實邊界部段節點數為9552,單元數為9284。軸壓工況載荷F=5.0 kN,彎曲工況載荷M=6250.0 kN·mm,組合工況載荷F=5.0 kN。有限元分析之后,提取主承力筒殼結構距離50 mm上邊緣處的節點位移作為主承力筒殼結構的位移響應。如圖1所示。
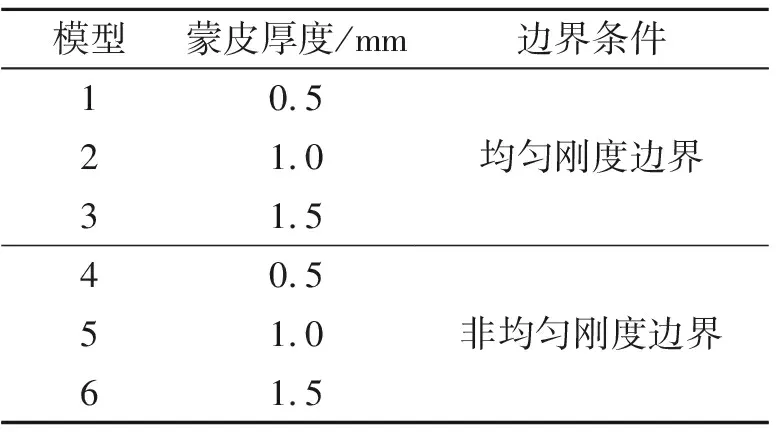
表1 彈性邊界設計算例
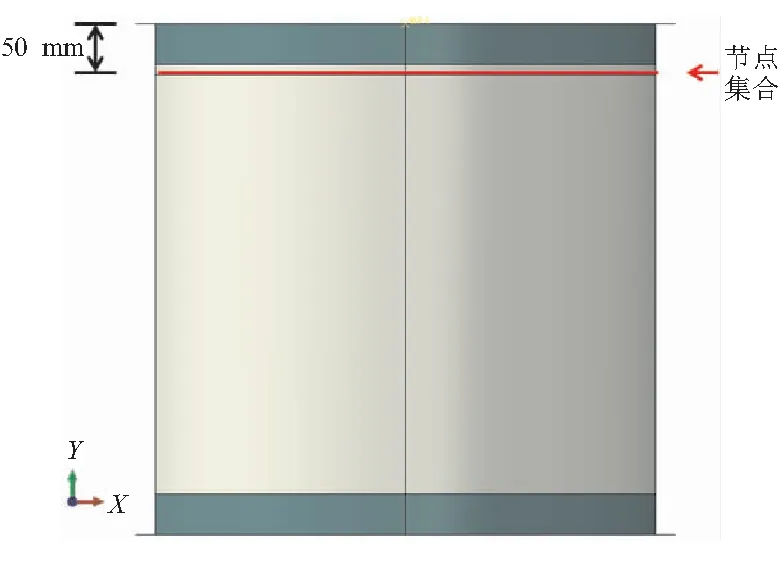
圖1 主承力筒殼結構邊緣處的位移響應
通過數值算例分析,得到主承力筒殼結構邊緣處的位移響應如圖2所示。對于軸壓工況,均勻剛度彈性邊界對應的軸向位移為一條直線,剛度分布均勻,而真實彈性邊界的軸向位移近似為正弦曲線,剛度分布非均勻,故選擇軸向位移為剛度等效指標,如圖2(a)所示。對于彎曲剛度工況,均勻剛度彈性邊界的徑向位移呈近似正弦曲線,而真實彈性邊界的徑向位移較均勻剛度彈性邊界有顯著的波動,故選擇徑向位移為剛度等效指標,如圖2(b)所示。對于組合載荷工況(軸壓+彎曲),均勻剛度彈性邊界與真實彈性邊界的軸向位移和徑向位移均有顯著的不同,故選擇軸向位移和徑向位移為剛度等效指標,如圖2(c)、(d)所示。
綜上所述,軸壓工況剛度的等效指標為軸向位移;彎曲工況的剛度等效指標為徑向位移;組合工況的剛度等效指標為軸向位移、徑向位移。
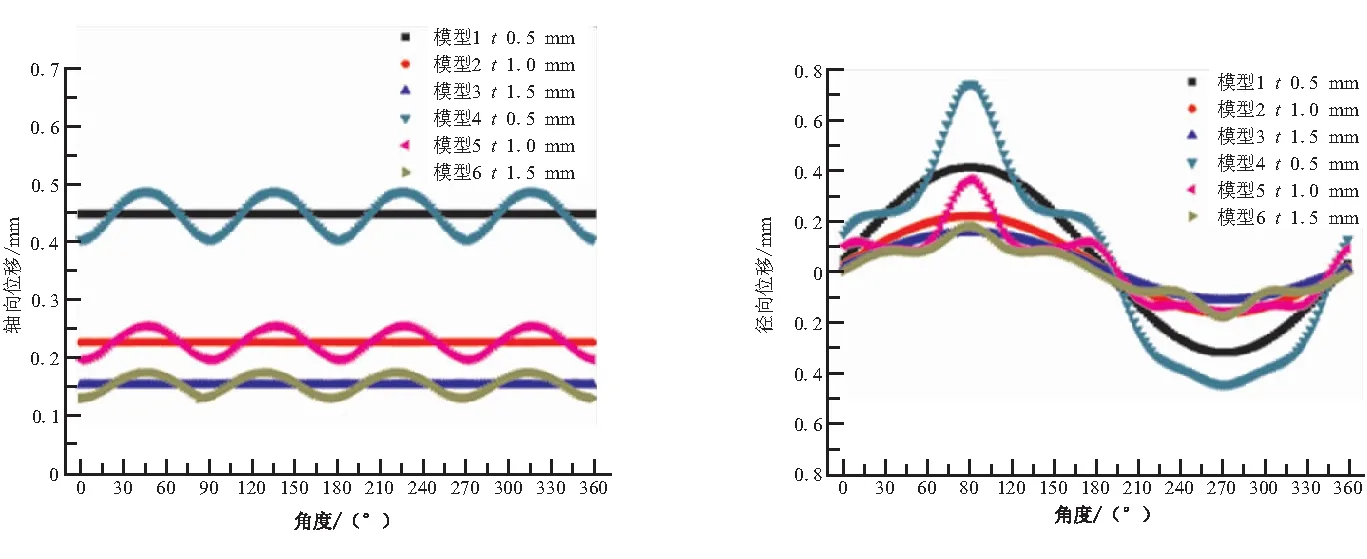
(a)軸壓工況軸向位移 (b)彎曲工況徑向位移
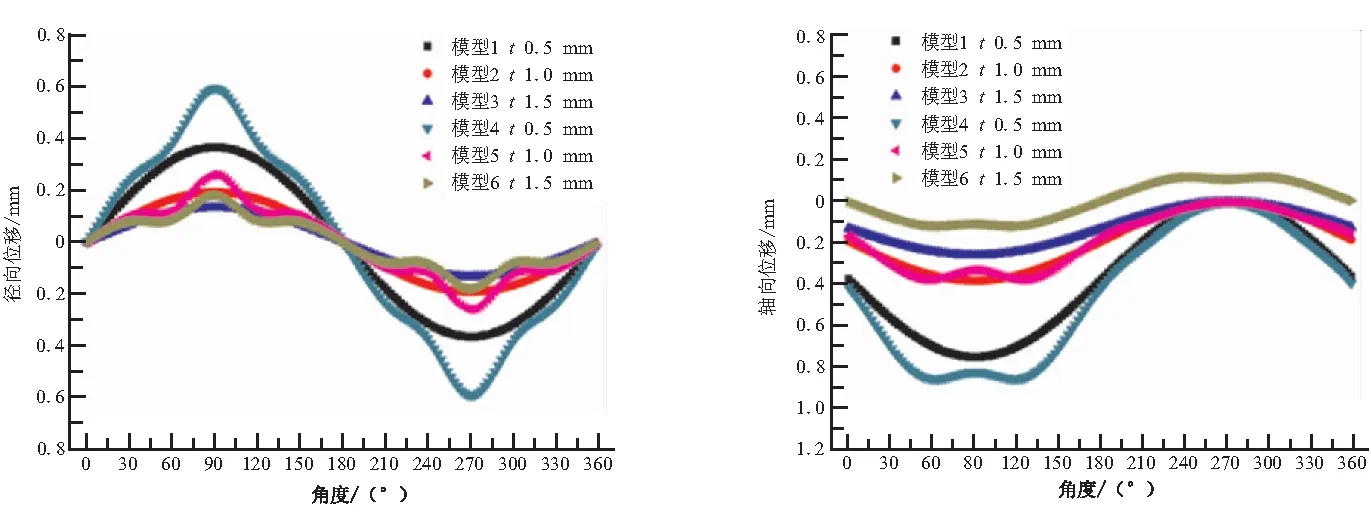
(c)組合工況徑向位移 (d)組合工況軸向位移
2 非均勻剛度彈性邊界優化設計
基于以上等效剛度指標,建立了非均勻剛度彈性邊界結構優化設計列式。以均勻剛度邊界的縱向桁條的分布角度為設計變量,以等效剛度指標的均方差最小為設計目標,開展優化設計。當設計目標值趨近于零時,認為非均勻剛度彈性邊界與真實的結構邊界相一致。此外,根據所得到的等效指標,建立了不同設計目標。優化列式如下:
(1)
式中αi為桁條分布角度;σi為各節點的剛度等效指標的均方差;σ為各節點的剛度等效指標的均方差之和;N為節點數目;n為桁條數目。
為了減少設計變量,提高優化效率,引入式(2)來描述桁條分布角度函數。
(2)
式中L為桁條分布角度之和;nj為桁條數目;λi為分布指數。
因此,設計變量轉化λi和nj。為考慮到結構的對稱性,L=45°。當λi=1的時候,桁條均勻分布;當λi≠1的時候,桁條呈指數分布,在[0,L]的區間由稀疏到密集。
表2給出了優化設計空間及最優設計。圖3給出了均勻剛度邊界及設計變量分布。
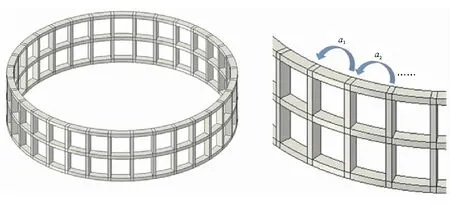
(a)均勻剛度邊界 (b)設計變量分布
軸壓工況、彎曲工況和組合工況下,優化設計目標(軸向位移的均方差)最優解分別為0.000 6、0.038 4、0.078 9,說明該優化設計目標與真實彈性邊界吻合較好。此外,軸壓工況、彎曲工況和組合工況下,優化設計的剛度等效指標的曲線與真實彈性邊界的曲線吻合較好(如圖4~圖6),說明了提出的優化設計方法及剛度等效指標的有效性。
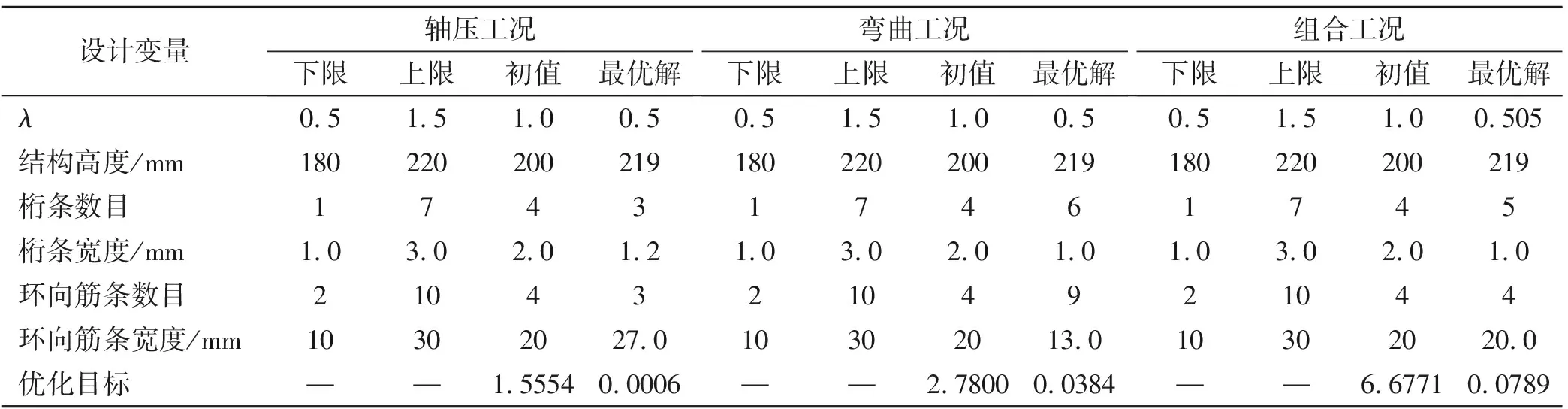
表2 優化設計空間及最優解
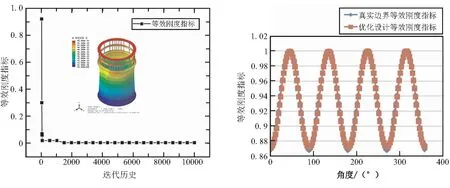
(a)軸壓工況迭代曲線 (b)軸壓工況軸壓位移曲線對比
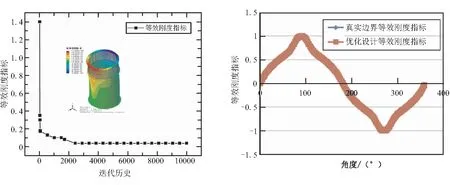
(a)彎曲工況迭代曲線 (b)彎曲工況徑向位移曲線對比
3 非均勻剛度彈性邊界原理性實驗
為進一步驗證非均勻剛度彈性邊界結構優化設計方法的有效性,開展非均勻剛度彈性邊界優化設計原理性實驗。實驗思路:通過對比真實邊界結構與優化設計得到非均勻剛度彈性邊界結構的應力水平,驗證該設計方法的可行性。
等效剛度邊界設計方法原理性實驗的實驗試件如圖7所示。實驗方案由試件,工裝和加載器組成。等效剛度邊界設計方法原理性實驗的實驗方案圖8所示。實驗試件及工裝等均采用鋼Q235,這是為了便于結構加工制造。考慮到軸壓載荷便于實驗加載,因此僅驗證軸壓載荷工況下等效剛度邊界工裝的傳力路徑。原理性實驗中的軸壓載荷為50 kN。
試件A為主承力筒殼結構,結構參數為H=510 mm,R=250 mm,t2=1.0 mm,h1=20 mm,b1=40 mm,t1=3 mm;試件B為真實彈性邊界結構,結構參數為H=510 mm,R=250 mm,t2=2.0 mm,h1=20 mm,b1=40 mm,t1=3 mm,開孔尺寸為250 mm×150 mm;試件C為傳統的均勻剛度彈性邊界結構,試件D為優化設計的非均勻剛度彈性邊界結構,參數見表2軸壓工況算例初值和優化值。
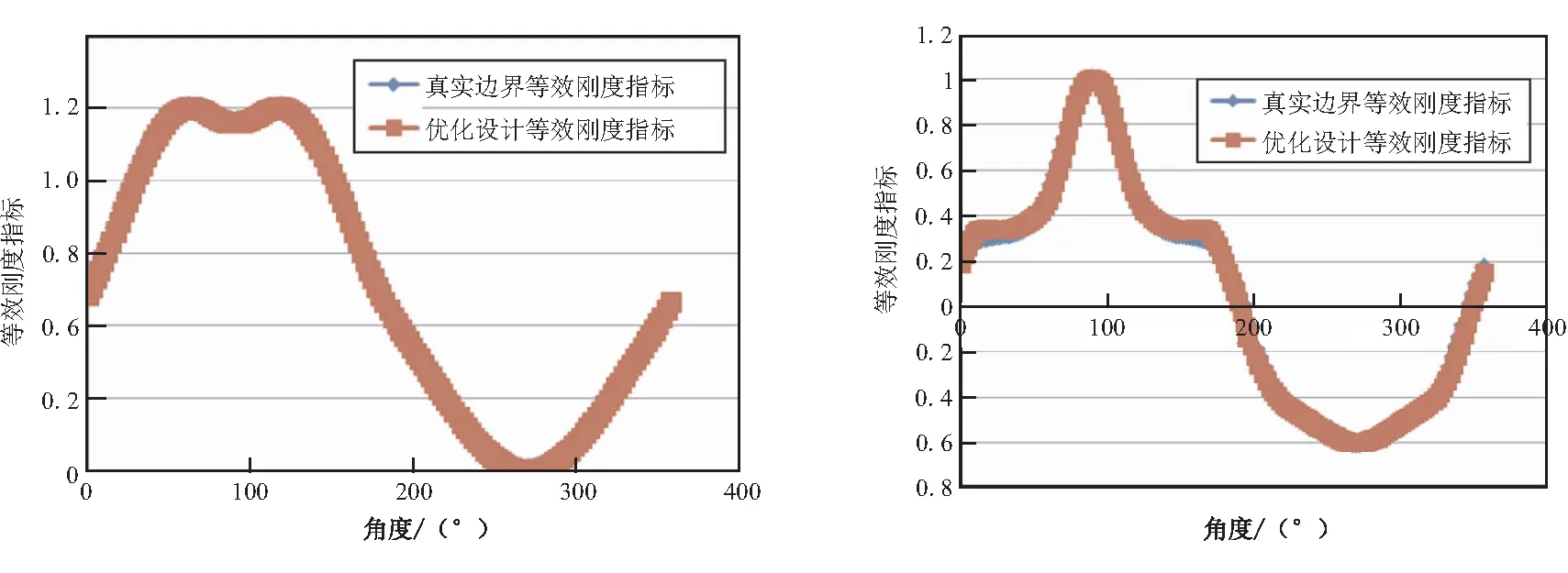
(a)組合工況軸向位移曲線對比 (b)組合工況徑向位移曲線對比
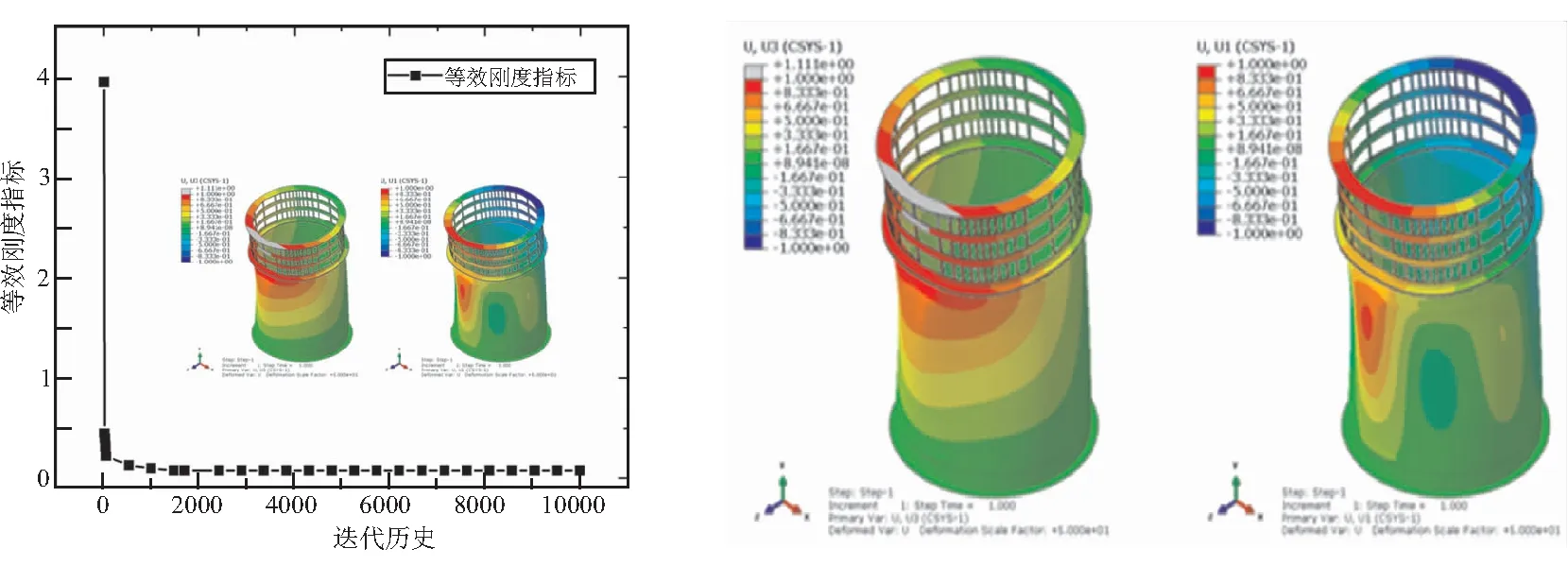
(c)組合工況迭代曲線 (d)軸向位移及徑向位移分布
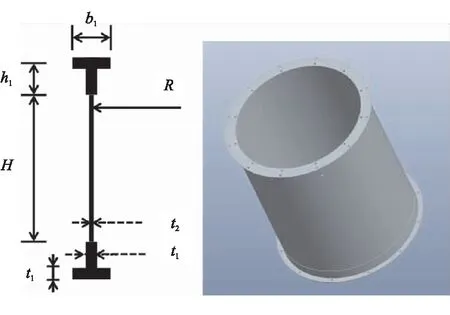
圖7 試件結構參數
圖9給出了數值預測及實驗結果對比,均勻剛度彈性邊界(實驗1)觀測的應力分布較均勻(如Test-1-Single),而真實彈性邊界(實驗2)和優化設計彈性邊界(實驗3)的應力分布相同(如Test-2-Combined和Test-3-Opt)。實驗1和實驗2的應力分布不相同說明均勻工裝和真實邊界工裝的傳力效果不同,應變的平均誤差為-22.29%。實驗2和實驗3的應力分布相同,且平均誤差為-13.70%,說明等效剛度邊界可以模擬真實邊界工裝的傳力效果。

圖8 實驗方案
圖9(b)給出了數值預測應力分布,該數值預測是模擬真實邊界工裝的傳力路徑算例的應力分布。數值預測與實驗2的應力分布相同,平均誤差為-16.88%,略高于實驗2和實驗3的平均誤差。數值預測與實驗結果不同的原因是實驗過程中存在不可避免的實驗誤差,主要為實驗蒙皮與端框的焊點不均導致應力分布不均勻,采樣點處受到更大的應力值。這也是實驗1的應力分布非絕對均勻的原因。
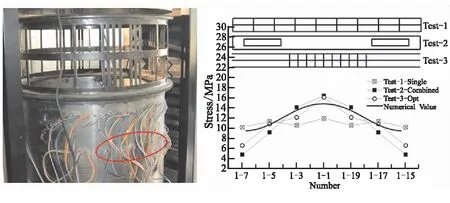
(a)應變片位置 (b)結構應力分布
4 結論
(1)通過開展剛度等效指標研究、考慮剛度等效指標的非均勻剛度彈性邊界優化設計研究以及原理性實驗研究,提出了非均勻剛度彈性邊界結構的優化設計流程,解決了傳統均勻剛度彈性邊界造成的載荷分配不均勻的問題。
(2)對于航天領域常見的三種工況(軸壓工況、彎曲工況和組合工況),提出了剛度等效指標來描述不同工況下非均勻彈性邊界結構的響應,為進一步的優化設計流程提供優化目標。
(3)對于非均勻彈性邊界結構優化問題,提出了基于剛度等效指標的非均勻彈性邊界結構優化列式。該優化設計列式可以考慮不同載荷工況下的剛度等效指標,實現非均勻剛度彈性邊界的優化設計。為提高優化設計效率,提出了引入指數函數來描述桁條分布規律,簡化了設計變量,大幅提高了優化設計效率。
(4)為進一步驗證非均勻剛度彈性邊界結構優化設計方法的有效性,開展了非均勻剛度彈性邊界優化設計原理性實驗。實驗結果顯示,優化設計結果與真實彈性邊界結果基本一致,驗證了等效剛度邊界設計方法的有效性。

