金字塔型點陣材料夾芯板抗爆性能仿真與優化

亓 昌， 郝鵬程， 舒 劍， 楊 姝

(大連理工大學 汽車工程學院，遼寧 大連 116024)

高孔隙率和變化多樣的微結構使得點陣材料具有獨特而優良的力學性能，諸如比強度大，比剛度高，以及非常理想的抗沖擊性能。常見的點陣材料拓撲結構主要包括四面體型，金字塔型，Kagome和Lattice block構架等[1]。金屬點陣材料夾芯板是以點陣金屬作為芯體，外加兩層較薄的金屬面板組成的復合結構，既能充分發揮點陣材料輕質、吸能等優點，又能利用面板提供所需的結構剛度并對芯體形成保護。

隨著現代軍用裝備機動與防護并重的發展需求，金屬點陣材料夾芯板在軍用裝備防護，尤其是爆炸防護方面的應用研究也逐漸增多。相比于其他拓撲結構點陣材料，金字塔型點陣復合材料除輕質、高強特性外,還具有隔熱、隔振和電子屏蔽等多功能可設計性,是極具潛力的先進多功能材料[2]。國內外學者對金字塔型點陣夾芯結構在爆炸載荷作用下的力學響應進行了較多研究，Dharmasena等[3-5]結合實驗與仿真，分別研究了金字塔型點陣夾芯結構在空氣、水下及沙土等介質中的爆炸沖擊響應，同時分析了具有不同厚度面板的夾芯板在炸藥處于不同距離下的變形及失效模式；Wei等[6]綜合采用實驗測試、有限元仿真和理論解析等多種方法，研究了多層金字塔點陣夾芯結構在爆炸載荷下的動態響應特性；朱凌雪等[7]提出了芯體截面梯度變化的金字塔型點陣夾芯結構，并通過理論分析和數值仿真證明了該結構面比吸能和壓潰載荷率優于傳統點陣夾層結構；王同銀等[8]提出了面板上薄下厚、芯體層上粗下細的功能梯度金字塔型點陣夾芯結構，并利用數值仿真證實了新結構可進一步提高金字塔型點陣夾芯結構抗爆性能。

在金字塔型點陣夾芯結構性能優化方面，Xue等[9]研究了金字塔型點陣材料、方形蜂窩和波紋板三種芯體夾芯結構的抗爆性能，并以各自的幾何參數為設計變量進行了以輕量化為目標的優化；Lee等[10]利用連續變焦遺傳算法對金字塔型點陣夾芯結構中內部芯子截面進行了形狀優化以增強其壓縮性能；Liu等[11]采用均質化方法并結合理論解析，優化了金字塔型點陣夾芯結構在承受彎曲、橫向剪切和面內壓縮等工況下的機械性能；易建坤等[12]利用ALE方法模擬爆炸載荷加載，分析了幾何參數對填充鋁泡沫的金字塔型點陣金屬夾芯結構抗爆性能的影響，指出了優化設計方向；泮世東等[13]提出了芯體與面板結合強度與芯體強度協調優化的思路，并對面外剪切載荷作用下的金字塔型點陣夾芯結構進行了優化設計，提高了其整體等效剪切強度。截至目前，涉及爆炸載荷下金字塔型點陣夾芯結構多目標優化與可靠性的研究尚不多見。

本文首先建立了用于金字塔型點陣金屬夾芯板爆炸沖擊響應仿真的詳細有限元實體模型和簡化梁單元計算模型；其次，基于Dharmasena等研究中的實驗數據驗證了模型的有效性和準確性；然后，利用仿真計算分析了芯體結構設計變量對夾芯板抗爆性能的影響規律；最后，以背板變形量、吸能特性及輕量化為目標，通過建立徑向基函數近似模型，對本文中基準金字塔型點陣夾芯板進行了多目標優化設計與針對不確定載荷的可靠性研究。

1 數值模擬

1.1 物理模型

金字塔型點陣材料夾芯板(Pyramidal Lattice Sandwich Panel，PLSP) 基準物理模型如圖1所示。夾芯板由上下面板和金字塔型點陣材料芯體(Pyramidal Lattice Core，PLC)組成。其中，上下面板分別對應結構的迎爆板(Front face)和背板(Back face)。面板與芯體均采用AL6XN不銹鋼。面板邊長L=420 mm，上下面板厚度tf=tb=1.52 mm，芯體厚度Hc=25 mm，炸藥當量設為200 g TNT，炸高h=150 mm。金字塔型芯體單胞構型如圖2所示，胞元底邊長l=35 mm，其腹桿截面為正方形，截面邊長tc×tc=1.9×1.9 mm，腹桿與面板的夾角α=45 °。

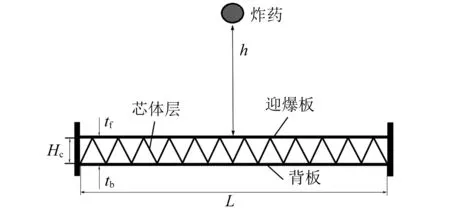
圖1 爆炸載荷下的金字塔型點陣材料夾芯板物理模型Fig.1 Physical model of PLSP under blast loading

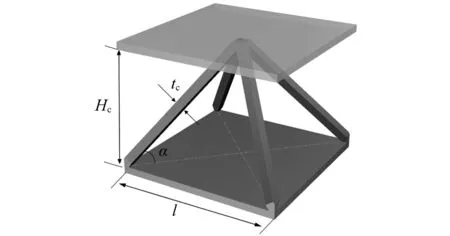
圖2 金字塔芯體單胞結構及尺寸Fig.2 Unit cell structure and size

1.2 有限元模型

基于顯式動力學分析軟件LS-DYNA，在前處理軟件Hypermesh中建立有限元分析模型。考慮結構對稱性，為節約計算時間，采用1/4模型并設置對稱約束邊界條件。面板采用4節點Belytschko_Wong_Chiang殼單元，芯體腹桿則分別采用六面體型實體單元(Element_Solid)與三維梁單元(Element_ Beam)劃分網格。對芯體定義自動單面接觸，面板和芯體間采用Contact_Tied_Surface_To_Surface接觸模型模擬焊接。考慮到文獻實驗中未發生焊點失效現象，仿真模型中不考慮焊點失效。Dharmasena等研究中金字塔型夾芯板爆炸實驗中板四邊采用螺栓固定，并支承在工字型支架上。相應地，有限元模型中采用周邊全約束，即將夾芯板四周各節點的3個平移和3個轉動自由度均設為零。爆炸載荷采用CONWEP算法模擬，并通過設置關鍵字Load_Shell加載到上面板上。仿真時間設為3 ms。夾層板材料AL6XN不銹鋼的主要性能參數總結于表1，采用分段線性塑性材料本構模型(Mat_Piecewise_Linear_ Plasticity)，失效塑性應變設為0.4。材料在不同應變率下的真實應力—應變曲線如圖3所示。

表1 夾芯板材料主要性能參數Tab.1 Mechanical properties of sandwich material

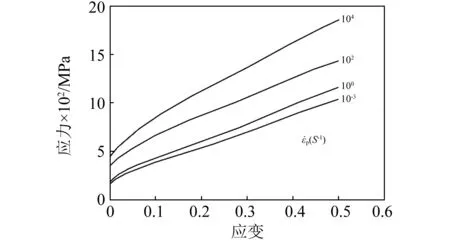
圖3 不同應變率下AL6XN不銹鋼應力-應變曲線Fig.3 Stress-strain curves of AL6XN under different strain rates

1.3 仿真模型簡化

在點陣材料夾芯結構有限元模型中，芯體一般采用實體單元建模以仿真詳細變形過程[14]。采用詳細實體單元模型的單次仿真計算時間一般尚可接受，但若涉及優化設計，實體單元模型的計算規模和計算時間往往難以接受。此外，實體單元對模型的參數化要求更高，不利于開展優化設計。考慮到三維梁單元能很好地反映截面屬性且易于實現模型參數化，因此，采用簡化梁單元替代實體單元對芯體腹桿進行建模，如圖4所示。兩種模型的節點數、單元數以及在4核英特爾xeon處理器上的單次仿真求解時間對比于表2。與實體單元模型相比，梁單元簡化模型規模僅為前者的3.8%，仿真計算時間不到前者的1%，計算效率大大提高，為點陣夾芯結構抗爆性優化設計提供了可能性和便利條件。簡化模型的等效性和仿真精度將在后文做進一步分析。

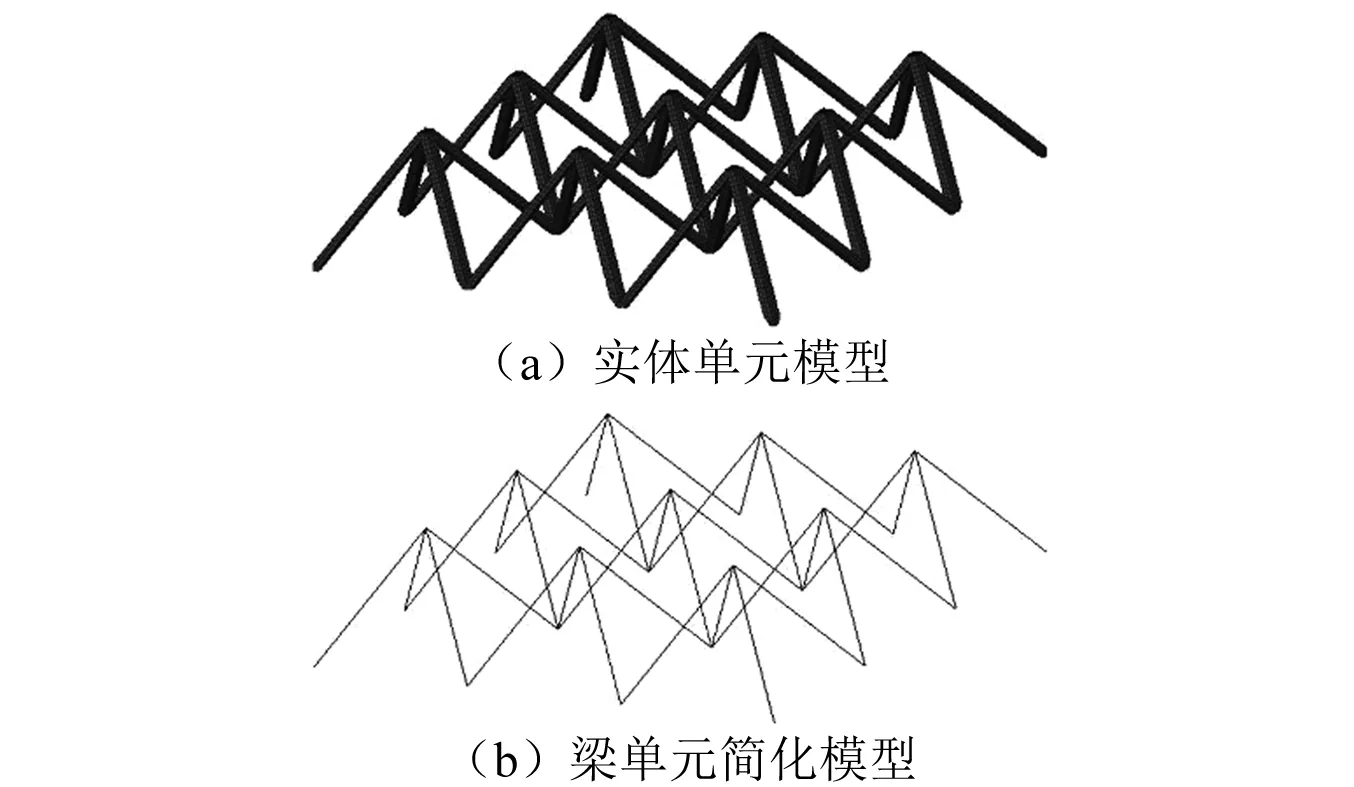
圖4 實體單元和簡化梁單元芯體有限元模型Fig.4 Solid element and beam element FE model of lattice core

模型類型節點數單元數計算時間/min1/4實體單元模型113 24890 8644061/4梁單元簡化模型4 3323 4564

1.4 抗爆性能評價指標

夾芯板被用作爆炸防護結構時，背板一側倘若變形過大，會對與之接觸的被保護的人或物造成損害。因此，選取背板最大瞬時位移量MaxD作為夾芯結構抗爆性能關鍵評價指標。另外，作為裝甲車輛、艦船等的防爆結構時，夾芯板的吸能特性和輕量化水平也要重點考慮。面比吸能(Areal Specific Energy Absorption，ASEA)定義為單位面積質量結構吸收的能量[15]，這一指標一方面體現了結構吸能能力；另一方面也將重量考慮在內，可作為夾芯結構抗爆性能的另一個重要評價指標。ASEA可表示為

ASEA=En/MA

(1)

式中：MA為單位面積內的質量；En為結構的總吸能量。

2 仿真結果分析

2.1 有限元模型驗證

為驗證本文的有限元建模方法，提升仿真結果的可信度，依據Dharmasena等研究中給出的實驗條件建立有限元驗證模型。模型中各參數值與圖1所示基準模型均相同。仿真150 g C4炸藥在炸高分別為75 mm，150 mm和200 mm時的金字塔型點陣金屬夾芯板爆炸響應。圖5為炸高150 mm時兩種仿真模型預測的夾芯板在t=3 ms時刻的最終變形與實驗結果的對比。由圖5可知，最大變形均出現在板心，兩種仿真模型中芯體腹桿的變形模式也與實驗結果吻合良好。不同炸高下的背板最終變形量總結于表3；仿真值與實驗結果相對誤差均在6%以內。上述結果驗證了本文有限元建模方法的正確性和有效性。本例中，炸高為75 mm和150 mm時，與實體單元模型相比，梁單元簡化模型對背板最終變形量的預測值更接近實驗數據，說明在一定范圍內簡化模型也能夠準確地預測夾芯板爆炸響應，可以替代實體單元模型用于結構優化設計。在不影響仿真精度的前提下，簡化模型的仿真計算時間減少了99%(見表1)，對后續優化中的試驗設計提供了很大便利。

表3 仿真結果與實驗結果對比Tab.3 Comparison of simulation and experimental results

圖5 仿真與實驗結果對比Fig.5 Comparison of simulation and experimental results

2.2 芯體相對密度

點陣夾芯層的相對密度為點陣材料密度與制造點陣材料的基體材料密度之比，也即點陣夾芯材料腹桿體積與芯體所占空間總體積之比。參考圖2所示金字塔型點陣材料胞元，對于腹桿截面為正方形 (tc×tc)，腹桿和面板間夾角為α的點陣材料芯體層，其相對密度ρ*可表示為

(2)

2.3 胞元結構參數對抗爆性能的影響分析

芯體相對密度對夾芯結構抗爆性能影響顯著。由式(2)可知，胞元結構參數Hc，tc和l均會影響芯體相對密度。以下在基準模型尺寸基礎上，基于梁單元簡化模型仿真結果，采用單一變量法分別考察胞元各結構參數對夾芯板抗爆性能的影響。

首先，保持tc和l不變，研究芯體厚度Hc的影響。圖6為芯體厚度從20 mm增加到30 mm過程中背板最大變形量MaxD和面比吸能ASEA的變化過程擬合曲線。由圖可知，MaxD隨芯體厚度增加非線性增大，當芯體厚度從20 mm增加到30 mm時，MaxD從15.8 mm單調上升到17.0 mm，增加了7.6%。與此同時，面比吸能基本呈線性上升，變化范圍為3.614～3.803kJ/(kg·m2)，增加了5.2%。這是由于芯體厚度增加使得腹桿與面板夾角變大，芯體層密度增加(見式(2))，剛度增強，傳遞到背板的爆炸波能量增加，從而導致背板變形量增加；另一方面，厚度增加使得芯體腹桿變長，腹桿壓縮距離增大，吸能更多。

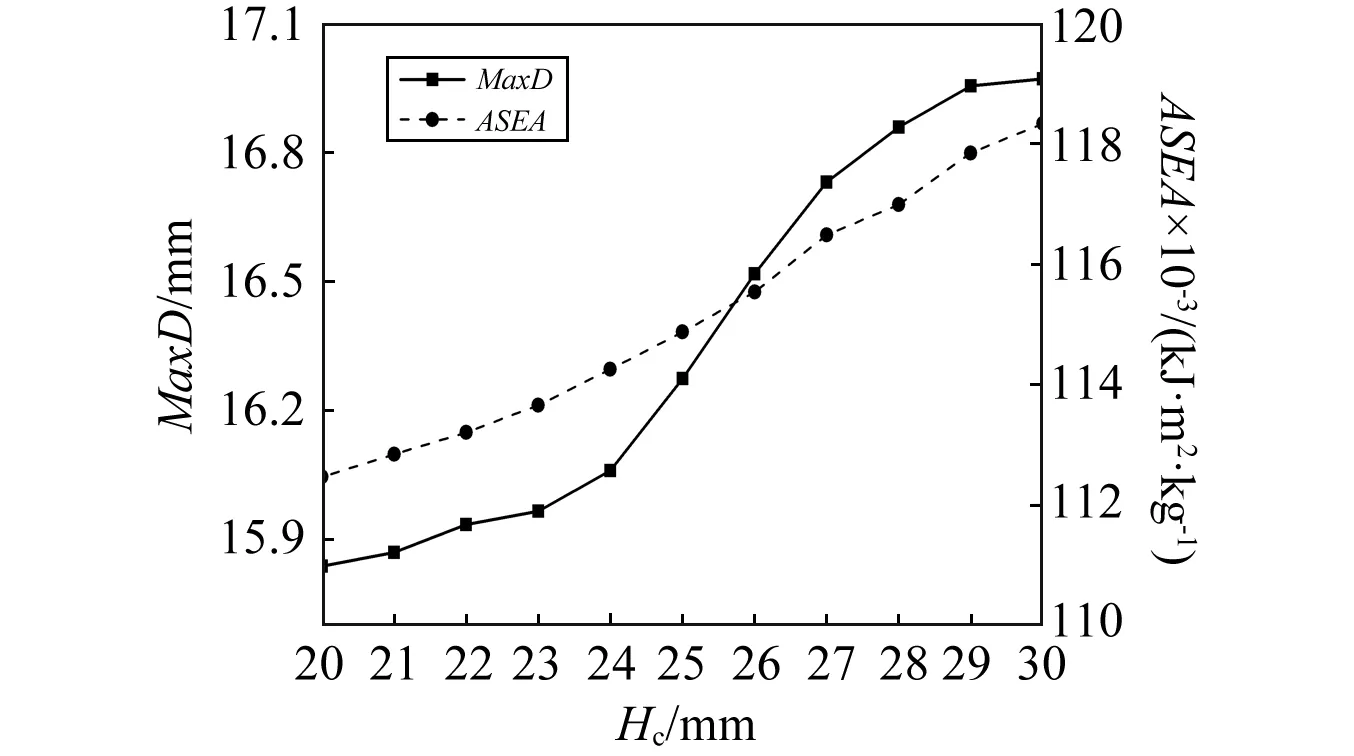
圖6 芯體厚度對PLSP抗爆性能指標的影響Fig.6 Effects of core thickness on blast-resistant indices of PLSP

其次，保持Hc和l不變，改變芯體腹桿截面邊長tc，研究其對抗爆性能的影響，結果如圖7所示。隨著芯體腹桿變粗，ASEA基本呈線性下降。這是由于芯體腹桿較粗，上面板厚度相對較小時，芯體腹桿不能被充分壓縮吸能。另一方面，腹桿變粗導致芯體相對密度增加，也會降低ASEA。此外，芯體腹桿過粗時面板成為主要吸能部件，易造成面板失效。與ASEA不同，MaxD隨tc增大呈現先增大后減小的趨勢，其原因在于當tc<2.1 mm時，背板主要呈現整體變形，隨腹桿強度增加，芯體層剛度增加導致吸能減少，傳遞到背板的爆炸波能量增加，背板最大變形量增加；當tc>2.1 mm后，由于腹桿強度過大，在爆炸沖擊下，芯體層并沒有起到足夠的緩沖作用，而是向下擠壓與背板連接的節點處，導致背板出現局部變形，最大變形量反而減小。

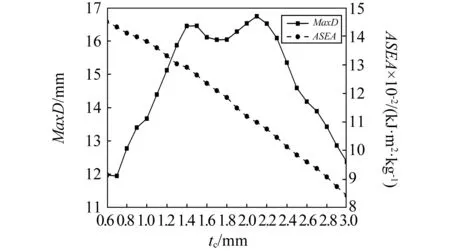
圖7 腹桿截面邊長對PLSP抗爆性能指標的影響Fig.7 Effects of side length of lattice bar cross section on blast-resistant indices of PLSP

最后，保持Hc和tc不變，研究胞元底邊長l的影響。為保證單胞結構完整性，設定l分別為42 mm，35 mm和30 mm，對應整個面板中單胞陣列數分別為10，12及14，腹桿與面板的夾角α則分別為40 °，45 °和50 °。仿真得到的各夾芯板變形模式近似，三種構型夾芯板的吸能和背板最大變形量時程曲線對比,如圖8所示。從圖8可知，胞元底邊長度對夾芯板抗爆性能影響明顯，一定范圍內，胞元底邊長減小，夾角α增大，單胞數量增加，芯體變“密”，阻礙芯體腹桿充分壓縮，吸能量減小；同時，腹桿與背板連接處節點數量增多，背板局部變形增大，導致背板整體變形減小，從而減小了背板最大變形量。當胞元底邊長l=35 mm，芯體腹桿與面板的角度為45 °，陣列數為12時，背板變形量與結構吸能均居中，綜合抗爆性能較好，可以此為基礎進行夾芯板優化設計。

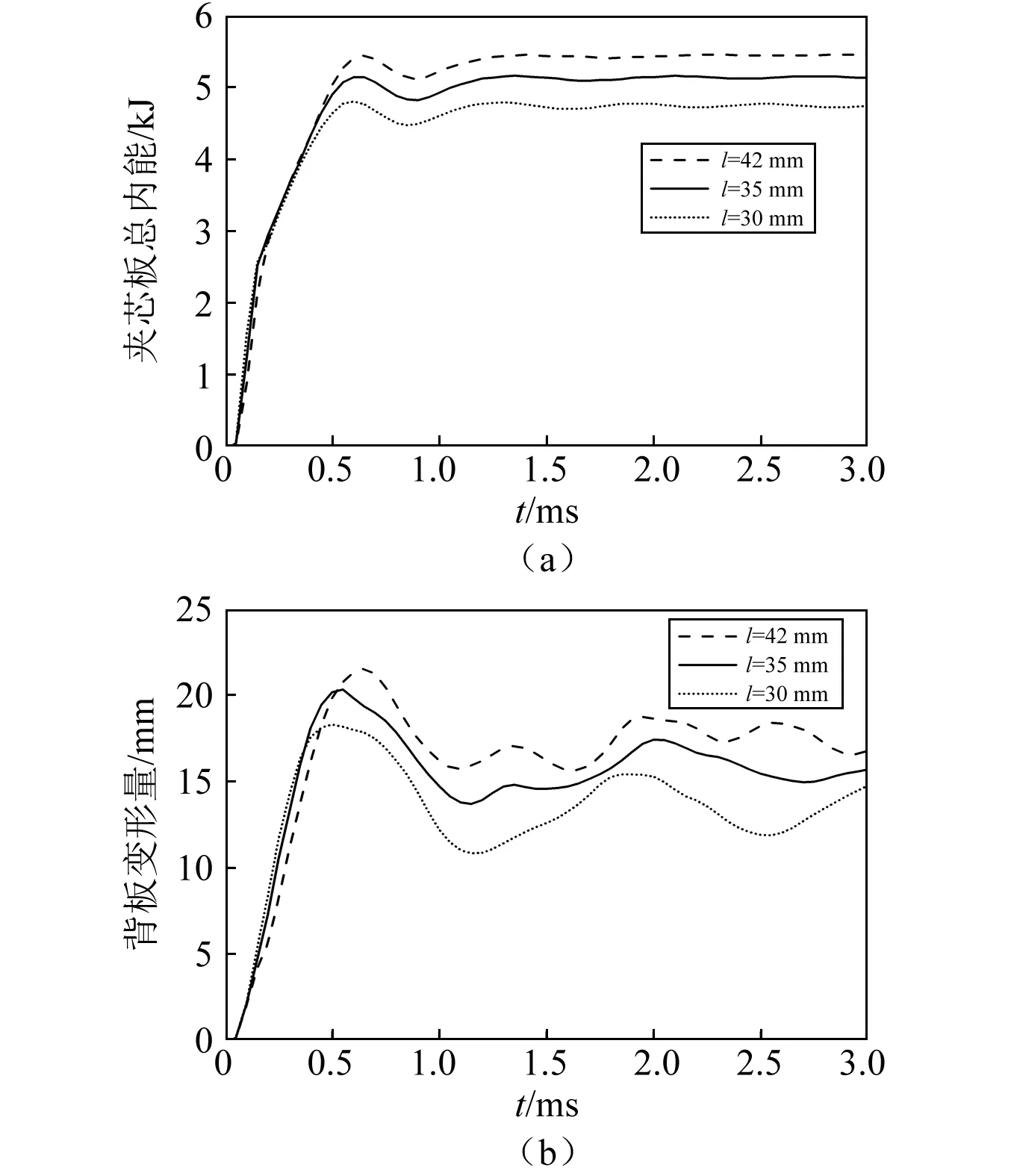
圖8 芯體胞元底邊長度對PLSP抗爆性能的影響Fig.8 Effects of bottom surface side length of unit cell on blast-resistance of PLSP

3 夾芯板抗爆性能多目標與可靠性優化

3.1 優化問題定義

考慮將PLSP應用于工程實際，對其進行優化設計。以軍車防雷應用為例，夾芯板附加于乘員艙底部，保護車內乘員不受地雷爆炸傷害。由于夾芯板背板厚度主要取決于車體底板，優化時將背板厚度設為定值tb=2 mm。在l=35 mm時的結構排布基礎上，以上面板厚度tf，芯體腹桿截面尺寸tc和芯體厚度Hc為設計變量，以面比吸能ASEA和背板最大變形量MaxD為目標函數，并且以夾芯板總重量為約束條件，定義PLSP多目標優化設計問題，其數學模型為

(3)

現實中，夾芯板所承受的爆炸載荷往往是不確定的，不同爆炸載荷下夾芯板響應差異很大。設計時如果忽略載荷不確定性，可能導致結構失效，降低夾芯板防爆性能設計的可靠性。為此，本文基于加權方法對夾芯板抗爆性能進行可靠性優化設計，通過給不同載荷賦予一個概率值，計算綜合各種設定載荷的目標函數期望值，其他約束條件不變。通過加權計算的面比吸能和背板最大變形量的期望值分別為[16]

(4)

(5)

式中：ASEAc和MaxDc分別為多種爆炸載荷下結構ASEA和MaxD的綜合加權值；ASEAi和MaxDi則分別代表第i種載荷下夾芯板的面比吸能和背板最大變形量；Wi為第i種載荷的發生概率，且有如下關系式

(6)

為方便討論，指定W1=W2=W3=1/3，尋求該概率分配下的設計最優解，其中W1,W2，W3分別代表200 g，300 g和400 g TNT當量爆炸載荷發生的概率。值得說明的是，此處的概率雖由人為設定，但不影響本文所提出的優化設計方法的一般性。

3.2 多目標優化結果

采用Sobol試驗設計(Design of Experiments,DOE)方法在設計域中抽取200個設計點，利用ANSYS APDL語言建立參數化仿真模型，并通過優化軟件集成流程自動完成不同載荷下200個DOE點的有限元分析，得到背板最大變形量MaxD和結構面比吸能ASEA，組成各載荷下的夾芯板優化初始DOE表。用于可靠性設計的初始種群抗爆性能指標是各種設定載荷下MaxD和ASEA的期望值，由式(4)、式(5)計算得到。建立徑向基函數(Radial Basis Function，RBF)響應面[17]，并預先在初始DOE點中留出5個測試點，進行響應面精度測試。表4為5個測試點的MaxD與ASEA仿真值與響應面預測值，以及預測值相對誤差。最大相對誤差僅為1.6%，說明所建立的響應面模型預測精度較高，可用于夾芯板的抗爆性多目標優化設計。

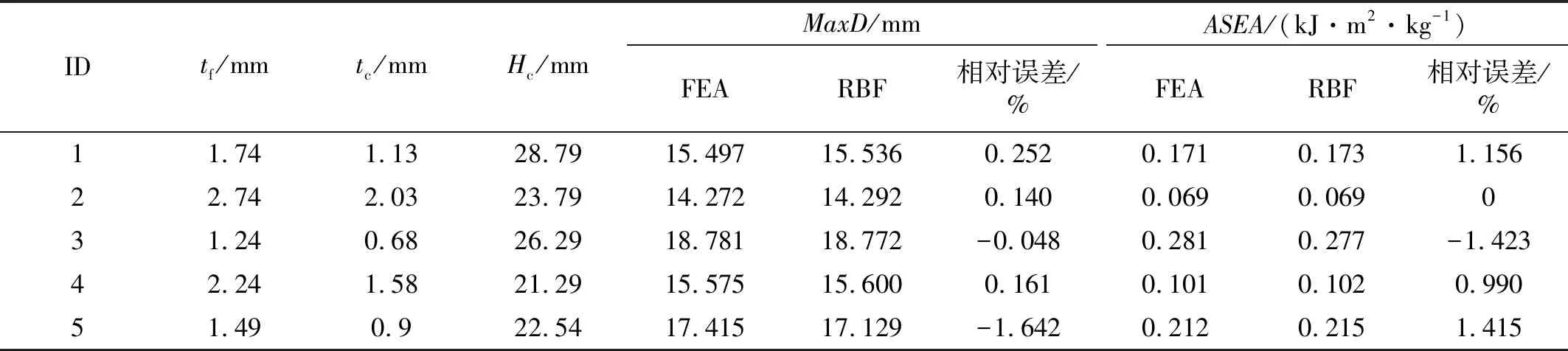
表4 5個測試點的仿真值、響應面預測值以及預測值相對誤差Tab.4 FEA and RBF response surface results of 5 testing points

基于RBF響應面，采用改進的非支配排序遺傳算法(NSGA-II)分別對三種爆炸當量(200 g，300 g和400 g TNT)下的PLSP進行優化設計，遺傳代數設為100，變異系數0.9，優化流程如圖9所示。計算得到對應不同載荷的式(3)中多目標優化問題的Pareto前沿，如圖10所示。提供了滿足不同設計需求的非受控最優解集。由圖10可知，三種載荷下夾芯板的兩個抗爆性能指標MaxD和ASEA無法兼顧，一個指標改善(惡化)的同時會導致另一個指標惡化(改善)。另外，對比三條Pareto前沿曲線可以看出，爆炸當量的增加會導致ASEA和MaxD同時增大，從而使相應的Pareto前沿向性能空間(-ASEAvs.MaxD)右下方移動。

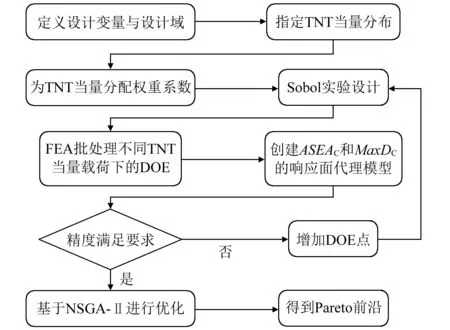
圖9 夾芯板抗爆性能多目標優化流程圖Fig.9 Flowchart of multi-objective optimization of PLSP

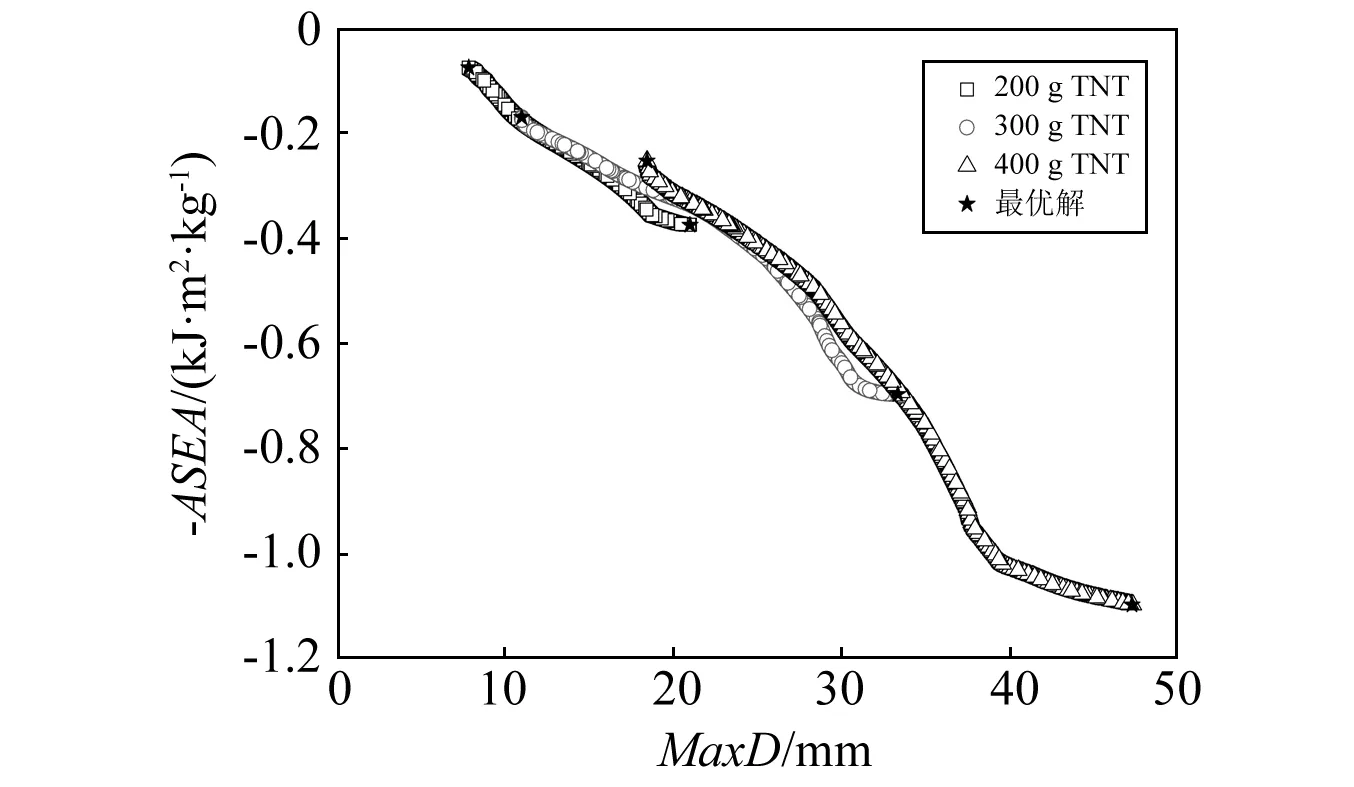
圖10 不同爆炸當量下PLSP的多目標優化Pareto前沿Fig.10 Pareto fronts for MDO of PLSP under blast loads with three intensities

表5列出了三種爆炸當量下PLSP的單目標理想最優解，即使得MaxD最小的解和使ASEA最大的解。可以看出，對應MaxD最小和ASEA最大的最優構型不同。三種載荷下最大ASEA對應的芯體厚度Hc和上面板厚度tf分別為各自取值范圍的上限(Hc=30 mm)和下限(tf=1 mm)。前者是由于芯體腹桿最長時壓縮空間最大，吸能增加；后者是由于上面板與芯體是主要的吸能組件，上面板“軟”有利于兩者均變形吸能。而對應不同載荷的腹桿截面邊長大致相同，說明tc和tf之間存在一個與外載荷無關的合理比值，使得夾芯板總體吸能水平最高，本例中，此比值約為1.1。另一方面，最小MaxD對應tf上限值，說明上面板“硬”有利于減小變形量；此外，tf與tc隨載荷強度的不同變化較大，說明載荷變化對最優解影響較大，即最優解的可靠性較差。

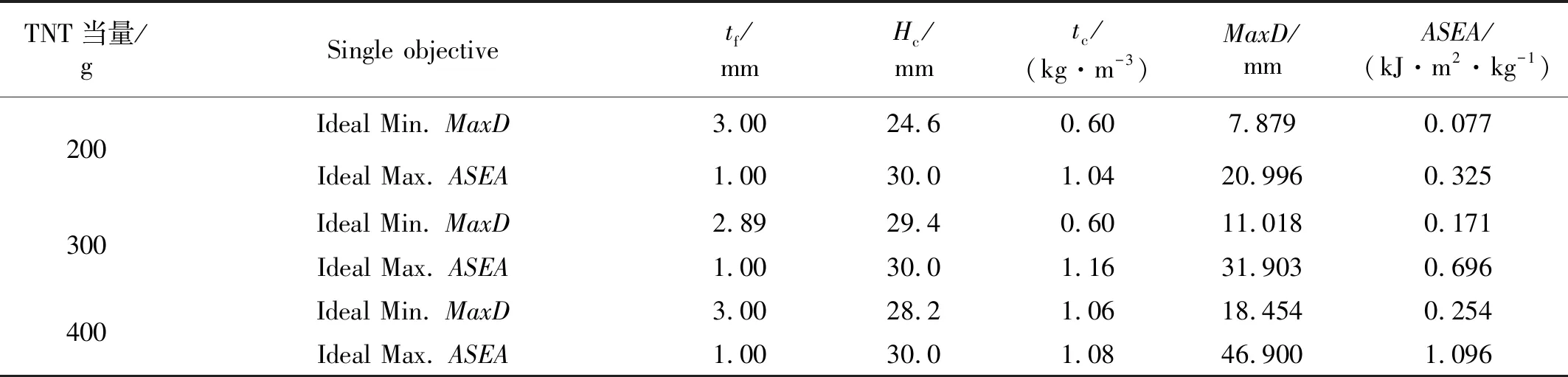
表5 三種爆炸載荷下PLSP的單目標理想最優解Tab.5 Single objective ideal optimal solution of PLSP under three explosive loads

3.3 可靠性優化結果

考慮載荷不確定性對夾芯板進行可靠性優化。如前所述，根據三種設定爆炸載荷下200個DOE點的仿真結果，按照W1=W2=W3=1/3計算得到考慮載荷不確定性的優化目標期望值ASEAc和MaxDc，并以此為訓練樣本建立RBF響應面模型。進而，以DOE設計作為初始種群，采用NSGA-II算法完成夾芯板抗爆性能可靠性優化，遺傳代數設為100，變異系數設為0.9。

夾芯板可靠性優化設計的Pareto前沿如圖11所示。由圖可知，MaxDc和ASEAc之間仍存在無法協同的矛盾，但Pareto前沿提供了考慮載荷不確定性的非受控(Non-dominated)解集。表6列出了考慮載荷不確定性的防爆性能單目標理想最優解。與單一載荷下的單目標最優設計對比可以看出，考慮載荷不確定性的可靠性設計中變量最優值和性能函數值沒有取到上下限和極值，這意味著設計結果為了抗爆性能的可靠性而選擇了妥協和折衷。

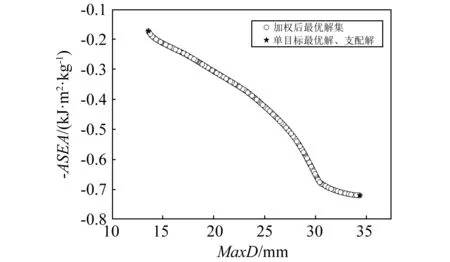
圖11 考慮載荷不確定性的PLSP多目標優化Pareto前沿Fig.11 Pareto front for MDO of PLSP under blast load uncertainty

表6 考慮載荷不確定性的PLSP的單目標理想最優解Tab.6 Single objective ideal optimal solution of the PLSP under uncertain blast load

4 結 論

(1)在保證計算精度的前提下合理使用簡化模型能大幅度減小仿真規模，縮短計算時間，為結構優化設計提供便利；在PLSP抗爆性能分析與優化中采用芯體梁單元簡化模型可達到上述目的。

(2)PLSP芯體關鍵幾何參數，包括：芯體厚度、腹桿截面邊長和胞元底邊長對其抗爆性能影響很大；其中，芯體厚度和腹桿截面邊長對ASEA的影響是線性單調的，但對MaxD的影響是非線性的。

(3)以關鍵結構尺寸為設計變量，以MaxD和ASEA為目標函數，基于RBF響應面模型和NSGA-II可以實現PLSP抗爆性多目標優化設計，得到Pareto最優解集，為設計方案選擇提供基礎。不同爆炸載荷下夾芯板Pareto前沿不同，但兩個抗爆性評價指標MaxD和ASEA均無法兼顧。

(4)通過設定不同載荷的發生概率，利用加權方法定義夾芯板MaxD和ASEA的期望值，可以實現考慮載荷不確定性的PLSP抗爆性能可靠性優化。可靠性最優設計有別于確定性載荷下的最優設計，一定程度上選擇了折衷方案。

值得說明的是，本文設定的載荷權重系數主要為說明可靠性優化方法，工程實際中應根據爆炸載荷強度概率分布研究確定。