基于隨機有限元的無砟軌道服役可靠性分析

李再幃， 張 斌， 雷曉燕， 高 亮

(1.上海工程技術大學 城市軌道交通學院, 上海 201620；2. 華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，南昌 330013；3. 北京交通大學 土木建筑工程學院, 北京 100044)

無砟軌道結構作為高速列車的行車基礎，其服役狀態直接關系到運營安全。在無砟軌道日常養護維修中，由于其扣件、軌道板、砂漿層等構件相對比較穩定，不易產生較大的變化，檢測與維修的重點往往集中于軌道幾何形位[1]。所以，研究和分析軌道不平順對無砟軌道服役可靠性的影響具有一定的理論價值和實踐意義。

為了深入的分析和控制無砟軌道服役可靠性，國內外學者從結構部件強度與設計理論、部件損傷、疲勞效應等多方面進行了研究，并采用了概率分析、一次二階矩、響應面等分析方法。如文獻[2]采用概率統計方法對Ⅲ型軌枕的可靠度及影響因素進行了討論。文獻[3]分析了在列車荷載及溫度梯度荷載作用下無砟軌道的橫向可靠度，利用一次二階矩法對可靠度指標進行驗算。文獻[4]利用多重疊合梁模型對CRTSⅡ型無砟軌道板產生開裂病害后結構可靠度進行分析，通過蒙特卡羅抽樣算法得到軌道板彈性模量、輪載等隨機變量的結構失效概率。文獻[5]基于可靠度理論構建了CRTSⅢ型無砟軌道結構耐久性與安全性評價體系，給出了混凝土碳化、凍融氯離子侵蝕等因素作用下結構的可靠度。文獻[6]則采用了響應面方法對無砟軌道結構部件損傷條件下結構的可靠性進行分析。文獻[7]分析了凍融條件下無砟軌道結構的疲勞可靠性度。這些研究得到了部分控制無砟軌道服役可靠性的因素及養護維修策略，深化了對無砟軌道服役可靠性的認識。但值得注意的是，上述研究多是利用相關結構設計參數展開，對目前相關維修檢測數據應用較少，且研究方法多采用確定性分析的方法，對隨機分析方法應用較少。與實際的無砟軌道結構服役狀態具有一定的差別。所以，有必要采用隨機理論相關方法對無砟軌道服役可靠性進行研究。

本研究利用車輛單元和軌道單元的有限元模型，采用神經網絡模型進行輪軌關系映射，利用輪軌動力學隨機因素構建無砟軌道服役極限狀態方程，通過蒙特卡洛混迭建模方法分析軌道不平順對無砟軌道服役可靠性的影響，從而實現對無砟軌道服役狀態進行定量化評估的目的。

1 無砟軌道結構可靠度相關概念

對無砟軌道服役可靠性而言，目前尚無一個統一的定義，既有規范和研究往往針對各自分析的問題進行概念界定。所以，根據相關成果[8-9]，本研究中將無砟軌道服役可靠性相關概念進行界定。

可靠性為無砟軌道結構在服役期限內保證列車安全平穩通過的能力。可靠度為可靠性的概率度量，即無砟軌道結構保證服役狀態的概率；與其對應的軌道結構失穩則為失效概率。當無砟軌道整體或部分構件超過某一特定狀態就不能滿足相關設計規定的車輛-軌道系統安全行車的要求，該特定狀態稱為無砟軌道服役極限狀態。

鑒于既有無砟軌道結構的偏安全性設計，在正常的服役限期內，其結構承載的應力與變形往往可以滿足列車安全運營的要求。因此，本研究這里引入了輪軌動力學隨機因素作為評判指標來評估無砟軌道服役狀態。在軌道隨機不平順的激勵下，輪軌系統的動力響應呈現了顯著的隨機特征[10]，其輪軌作用力可作為直接的特征向量。由于評估列車運行安全性標準中，多采用脫軌系數和傾覆系數作為評價指標[11]。所以，本文中這里采用這2個指標作為評估無砟軌道可靠性的標準,其對應的無砟軌道服役極限狀態方程為

(1)

(2)

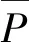
由上述兩式可知，在輪軌系統隨機因素(如軌道不平順等)作用下，尚無法用明確的解析表達式來表征相應的無砟軌道服役極限狀態方程，即方程隱式化問題。所以，本研究中，采用隨機有限元方法對此問題進行研究和分析。

2 基于隨機有限元-神經網絡-蒙特卡洛的混迭建模方法

一般而言，隨機有限元方法包含有限元一次二階矩法和有限元蒙特卡洛法，前者只適合于弱非線性系統，而后者則適用于極限狀態方程隱化的高度非線性系統[12]。因此，本研究中采用了有限元蒙特卡洛法進行分析求解，但由于此方法在求解節點數較多的非線性結構體系時，需要的運算量大、計算時間長的缺點，這里利用神經網絡非線性映射能力強的特點，對輪軌系統響應量與輸入量的映射關系進行逼近。

2.1 輪軌動力學有限元模型

利用有限元理論，建立車輛-軌道非線性耦合動力模型，將整個系統離散為車輛單元和軌道單元。其中，車輛單元為一個附有二系彈簧阻尼的多剛體動力系統，如圖1所示。軌道單元為路基上CRTS II 型板式無砟軌道，如圖2所示。

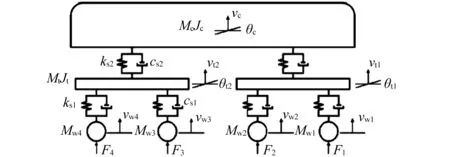
圖1 車輛單元模型Fig.1 Vehicle element model

圖1 中:Mc和Jc分別為車體質量與轉動慣量；Mt和Jt分別為轉向架質量與轉動慣量；Mwi(i=1, 2, 3, 4)為第i個車輪質量；ks1和cs1分別為車輛一系懸掛剛度與阻尼；ks2和cs2分別為車輛二系懸掛剛度與阻尼；vc和vti(i=1, 2)分別為車體和前后轉向架的沉浮運動豎向位移；θc和θti(i=1,2)分別為車體和前后轉向架的點頭運動角位移；vwi(i=1, 2, 3, 4)為第i個車輪的豎向位移；l1和l2分別為車輛固定軸距之半和車輛定距之半。

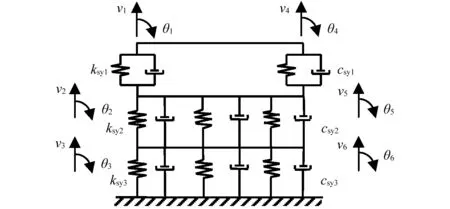
圖2 CRTS II型板式軌道單元模型Fig.2 Track element model of CRTS II

圖2中：u1和u4分別為鋼軌的豎向位移；θ1和θ4分別為鋼軌的轉角；u2和u5分別為預制軌道板的豎向位移；θ2和θ5分別為預制軌道板的轉角；u3和u6分別為水硬性混凝土支承層的豎向位移；θ3和θ6分別為水硬性混凝土支承層的轉角；ksy1，ksy2和ksy3分別為無砟軌道扣件、CA砂漿和防水層的剛度；csy1，csy2和csy3分別為無砟軌道扣件、CA砂漿和防水層的阻尼。

利用有限元集成法可形成車輛-軌道耦合系統總剛度矩陣K、總質量矩陣M和總阻尼矩陣C，得到車輛-軌道耦合系統動力有限元方程

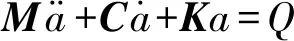
(3)

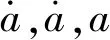
式(3)可以通過Newmark-β積分法實現數值求解[13-14]。

2.2 混迭計算模型

由式(3)可知，由于車輛及軌道單元節點數較多，特別是當軌道長度較長時，需要耗費大量機時進行輪軌動力學響應運算。而根據規范的可靠度指標的相關要求，應用蒙特卡洛法(MonteCarloSimulation，MCS)至少要進行1×105以上的運算次數，這無疑不利于對無砟軌道結構服役狀態的及時評定。因此，本文這里引入人工神經網絡模型對輪軌關系進行映射，以期在保證計算精度的前提下提高運算效率。

相關理論表明：在隱含層節點數充分大的情況下，單隱層的BP神經網絡可以以任意精度逼近任何一個具有有限間斷點的非線性函數。這里采用了三層BP神經網絡結構進行輪軌關系映射，其中，輸入變量為2種軌道不平順(高低及軌向)、輸出變量為2個即脫軌系數及輪重減載率極限狀態方程值。根據文獻成果與前期試算，將網絡結構選為2-5-2結構，即包含5個隱含節點。

在此基礎上，采用MCS進行計算，計算流程如圖3所示。

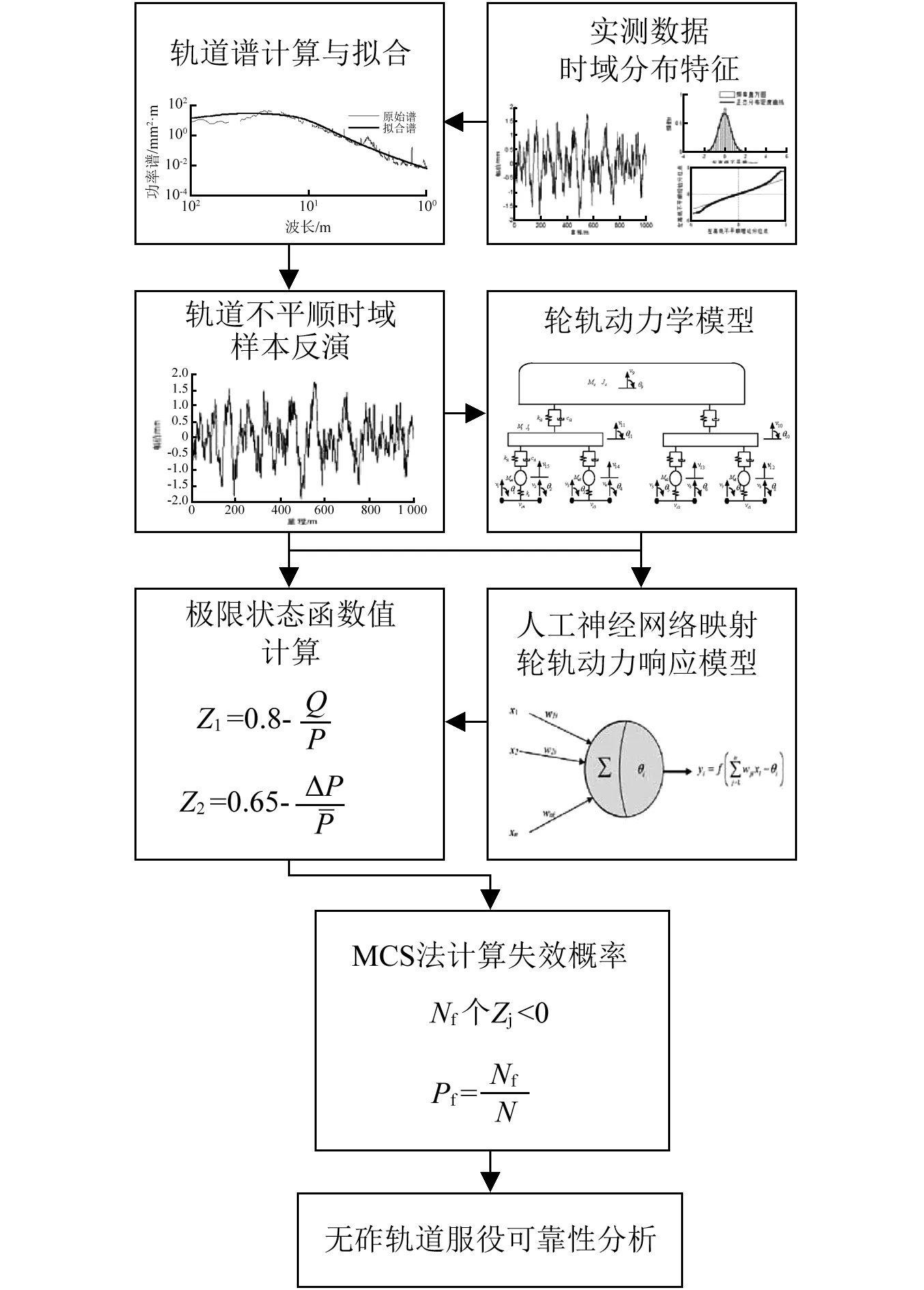
圖3 混疊建模計算流程Fig.3 Calculation flow of hybrid model

具體計算步驟為：

步驟1軌道不平順時域隨機樣本的生成，利用實測樣本進行隨機樣本的擬合與反演；

步驟2基于車輛-軌道單元的輪軌動力響應及極限狀態方程計算；

步驟3利用三層BP神經網絡進行輪軌映射關系構建；

步驟4對軌道不平順隨機量進行N次時域反演，并采用映射模型進行極限狀態方程值求解，得到N個Zj(j=1,2,…,N)值；

步驟5設在N個Zj中存在Nf個Zj<0，當N充分大時，無砟軌道結構的失效概率為

(4)

3 算 例

為了對本文所提分析方法進行驗證，這里采用如下算例：高速列車為標準CRH 3C型動車組、運行速度為350 km/h，軌道結構為CRTS II型板式無砟軌道，基礎為路基結構。

3.1 軌道不平順的擬合與時域反演

根據動檢車實測樣本進行軌道不平順統計特征計算，實測樣本如圖4所示。采用文獻[15]方法進行軌道不平順譜計算，獲得樣本軌道譜參數后，將其作為目標函數，并利用二進制小波方法進行樣本時域波形反演。

時域樣本的擬合結果和反演的時域樣本如圖5及圖6所示。所采用的目標擬合公式為中國鐵路7參數公式；擬合參數結果如表1所示。

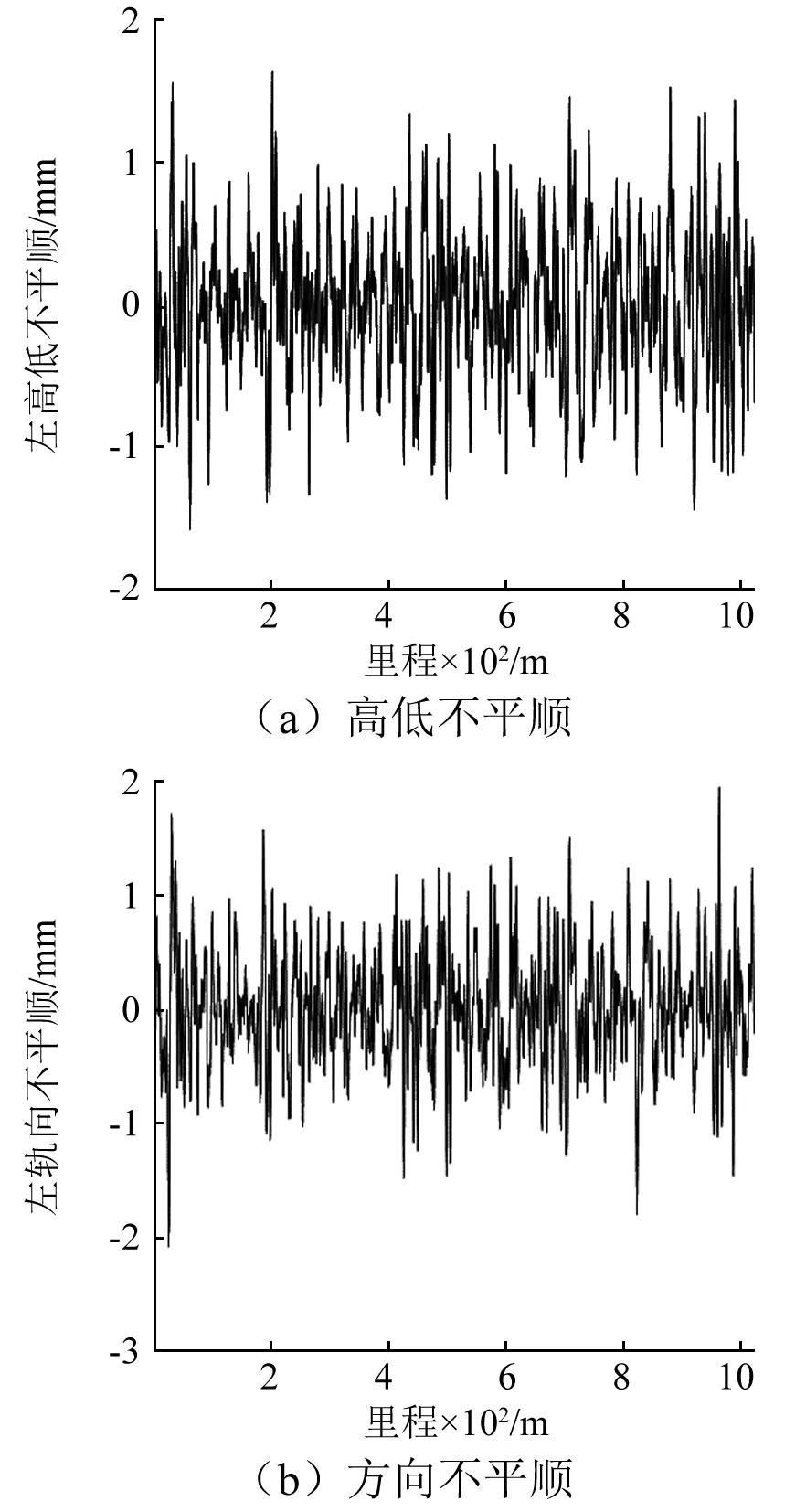
圖4 軌道不平順時域分布Fig.4 Time domain of track irregularity

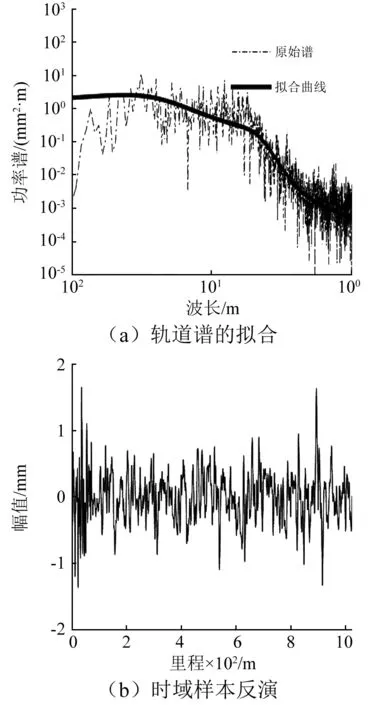
圖5 左高低不平順的擬合與時域反演Fig.5 Fitting and time domain inversion of left longitudinal irregularity

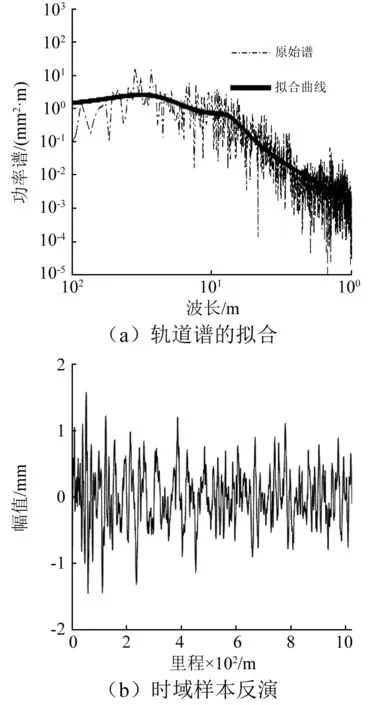
圖6 左軌向不平順的擬合與時域反演Fig.6 Fitting and time domain inversion of left alignment irregularity

參數ABCDEFG左高低0.000 35-0.611 990.136 97-0.408 770.056 36-0.002 920.000 09右高低0.000 67-0.685 120.159 21-0.449 30.066 8-0.002 640.000 07左軌向0.001 62 -0.208 84 0.016 93 -0.314 88 0.034 60 -0.001 45 0.000 03 右軌向0.001 77 -0.260 22 0.018 79 -0.320 41 0.035 00 -0.001 48 0.000 03

由以上圖表可知，所得的擬合譜參數可以較好地反映出原始軌道不平順的時頻特征。因此，采用表1參數進行軌道不平順時域波形的反演。

3.2 神經網絡模型的訓練

輸入變量為隨機生成的軌道不平順樣本，長度為1 000；輸出變量為對應輪軌動力計算得到的脫軌系數及輪重減載率極限狀態方程值。結果如圖7及圖8所示。

通過預先的大量試算，將BP神經網絡迭代次數設為100、學習率為0.005、網絡收斂目標為0.000 04。則神經網絡預測結果如圖9所示。

圖7 神經網絡計算輸入參量Fig.7 Inputs of BP neural network model

圖8 神經網絡計算輸出參量Fig.8 Outputs of BP neural network model

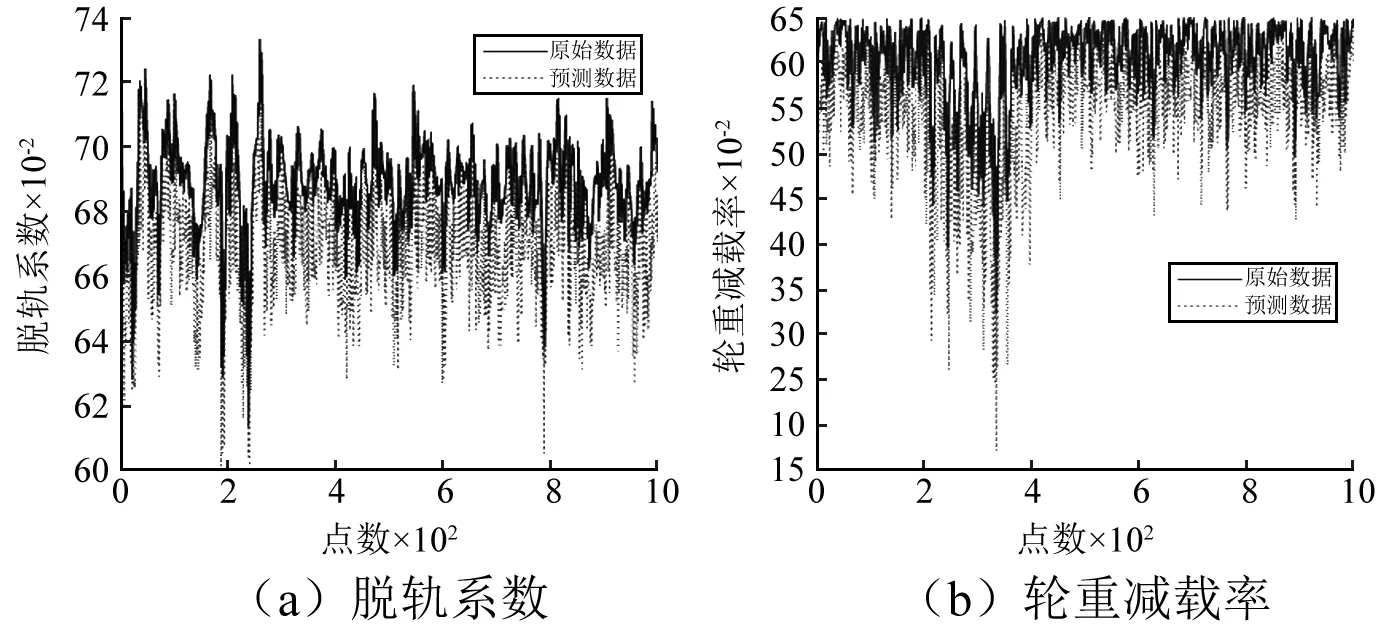
圖9 神經網絡模型預測結果Fig.9 Predictions of BP neural network model

由圖9可知，輪重減載率極限狀態方程值的預測樣本和實際樣本相關系數為0.805、誤差均方值為0.073，而脫軌系數極限狀態方程值的則相關系數為0.767、誤差均方值為0.023，說明預測樣本與實際樣本誤差較小、且呈現強烈相關的特性。對比實際數據與預測數據的樣本區間可知，兩者之間幅值區間差別較小。所以，綜上可得所采用的BP神經網絡模型較為真實地反映了實際數據的變化趨勢與幅值分布，可以采用BP神經網絡建模方法對軌道不平順與輪軌動力響應的關系進行映射，從而進行相應的動力計算，值得注意的是相關參數選擇是模型逼近準確性的關鍵要素。

3.3 計算結果

利用建立的輪軌系統BP神經網絡映射模型替代蒙特卡洛法中的輪軌動力學模型，進行無砟軌道結構服役安全性的可靠度和失效概率計算。

依據相關規范要求，CRTS II型板式無砟軌道屬于鐵路工程結構安全等級中的二級，對應的目標可靠度指標建議管理值為3.7即失效概率為1.078×10-4，則若要計算的可靠性指標滿足上述要求，則至少要進行以上的次數1×105，為了盡可能的逼近真實解析解，本文這里選取計算次數為1×105。

為了對比分析，同樣給出了利用傳統輪軌動力學模型進行計算的結果，如表2所示。

表2 BP神經網絡模型計算結果Tab.2 The calculations of BP neural network

通過上表可知，利用BP神經網絡法映射模型可以獲取軌道結構服役安全性的可靠指標和失效概率，所得的無砟軌道服役可靠性指標值滿足相關規范要求；其計算結果與采用傳統模型得到的近似解析解對比分析可知，所得的計算結果工況所計算精度較采用輪軌理論模型差，這主要是由于在BP神經網絡映射模型逼近求解過程中，產生累積誤差，導致其所計算的可靠指標有一定的偏差；但比較計算時間可知，采用BP神經網絡可以有效地節約計算時間，顯著地提升算法的效率。值得注意的是，由于BP神經網絡的建模過程中對參數依賴性較高，如參數優化不良，則會產生算法不收斂或收斂速度慢等問題，因此，此算法的普適性相對較差，應用前需要進行大量的參數試算。

綜上，當工程的要求精度不高或軌道服役狀態相對較好時，可以采用此方法進行相應的無砟軌道結構服役安全性檢算。

4 結 論

本文從輪軌動力學隨機因素構建無砟軌道服役極限狀態方程，采用輪軌動力學有限元、BP神經網絡和蒙特卡洛混迭建模的方法，分析了無砟軌道的服役可靠性，得到以下結論：

(1)無砟軌道服役可靠性評估需要考慮輪軌動力學作用。

(2)可以采用隨機有限元和神經網絡相結合的方法對無砟軌道結構服役可靠性進行定量計算。

(3)在現有的軌道不平順狀態水平下，無砟軌道結構服役狀態可以滿足高速列車安全運行的要求。

(4)建議將結構服役安全性驗算指標納入到養護維修體系中，以便更加全面有效地保證高速鐵路的運營安全。