基于小波包能量的地基土對框筒結構地震損傷影響試驗研究

沈 超， 錢德玲

(合肥工業大學 土木與水利工程學院，合肥 230009)

土-結構動力相互作用體系長期以來一直是國內外地震工程的研究熱點課題。文獻 [1-3] 表明：在地震作用下土-結構相互作用體系通過地基土的能量耗散減小了上部結構的動力響應和振動基頻。但現有研究成果中的上部結構形式較為簡單，多為單自由度體系或多自由度框架結構。對于實際高層框筒結構建筑，其地基土對上部結構的地震響應影響研究卻較為少見。相比結構振動反應量的最值分析，小波包能量分析不僅能通過振動波形分解、小波包系數和頻帶能量反映結構的振動強度、基頻和持時，還能通過能量變異最值指數反映結構的損傷情況。因此，采用小波包能量理論研究土-框筒結構高層建筑動力相互作用體系的地震響應具有十分重要的意義。

曹一龍等[4]采用小波包能量變異最值指數法對某八層混凝土框架結構振動臺試驗模型進行了損傷評定。中國生等[5]通過小波包能量分解理論，建立了爆破沖擊波作用下考慮振動強度、頻率和持時的建筑物結構安全評估判據。Suarez等[6]通過小波包能量分解計算得到了不同烈度地震作用下某新型軟鋼阻尼器的能量耗散特點，并結合能量變異最值指數分析了地震作用下安裝該新型阻尼器的混凝土框架結構損傷情況。

1 結構損傷的能量指標定義

1.1 小波包分解和小波能量

小波包分解是基于小波變換的一種信號分解精細算法，該算法不僅具有小波變換的信號低頻部分精確分解的優點，還能同時對高頻部分精確分解，從而大大提高信號分解的完整性。

假定某振動信號f(t)經過小波包的j層分解，每個分解信號x(t)可表達為[7]

(1)

其中，

(2)

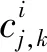
(3)

將分解信號x(t)的平方在無限域上積分即可得到信號f(t)的總能量

“那以后有機會再講，我還是將那個男人的故事說完吧。S的前妻好像不止一個，但小說家沒交待清楚，也許小說家也沒有搞清楚。那個男人又不是小說家塑造的人物。這可能是那個男人的隱私，超出了小說家的掌控。當然，跟S有染的異性之多就難以盡數了。”

(4)

(5)

(6)

1.2 能量變異最值指數

在地震荷載作用下，結構的損傷必然導致結構固有特性的變化，從而使得結構各頻帶能量發生重分布。通過對比損傷前后各頻帶能量的最大值，可直觀的反應結構的損傷程度變化。定義能量變異最值指數為

(7)

2 振動臺試驗簡介

2.1 模型的設計與制作

為使研究結果能夠更準確地反應地震作用下土對實際高層框筒建筑的損傷影響，試驗模型選用某41層框架-核心筒高層建筑作為模擬對象。采用抽層的方法對原型結構進行簡化，將各個標準層中相鄰的上下樓板抽去，并將所抽去樓板的恒活荷載平均分配至相鄰的上下層樓板，抽層過程如圖1所示。根據強度和剛度等效原理對柱和核心筒截面進行修正，并采用Buckingham π定理確定模型各參數的相似比例(見表1)。最終將41層的原型結構簡化為了縮尺比例為1/50的20層試驗模型[8-10]。

表1 模型相似比例

簡化后的試驗模型上部結構高度為3.566 m，下部結構為3×3的群樁基礎(見圖2)，圓樁樁徑0.08 m，樁長0.72 m，承臺板尺寸為0.92 m×0.92 m×0.1 m的立方體。模型上部結構主要構件尺寸，見表2所示。模型材料選用與原型建筑材料力學性能相近的微粒混凝土、鍍鋅鐵絲和鐵絲網分別模擬原型建筑的混凝土、縱筋和樓板鋼筋網[11-12]。

試驗采用柔性圓筒狀土箱裝填試驗用土，相比剛性土箱和層狀剪切型土箱，柔性土箱能最大程度的降低“模型箱效應”。該土箱直徑為3 m，土箱內試驗用土自下而上分別為0.5 m厚砂土、0.5 m厚砂質粉土和0.1 m厚粉質黏土。土箱的構造和試驗用土的粒徑，如圖3和圖4所示。

圖1 抽層過程Fig.1 The process of model simplifying

圖2 模型下部群樁基礎Fig.2 The view of the grouped piles foundation

樓層層高框架柱截面尺寸角柱邊柱梁截面尺寸主梁次梁樓板厚度剪力墻厚124055×5535×3545×3030×151560220655×5535×3545×3030×151560326455×5535×3545×3030×1515604～2016850×5035×3535×2025×151545

圖3 土箱結構示意圖Fig.3 The structure sketch of the soil box

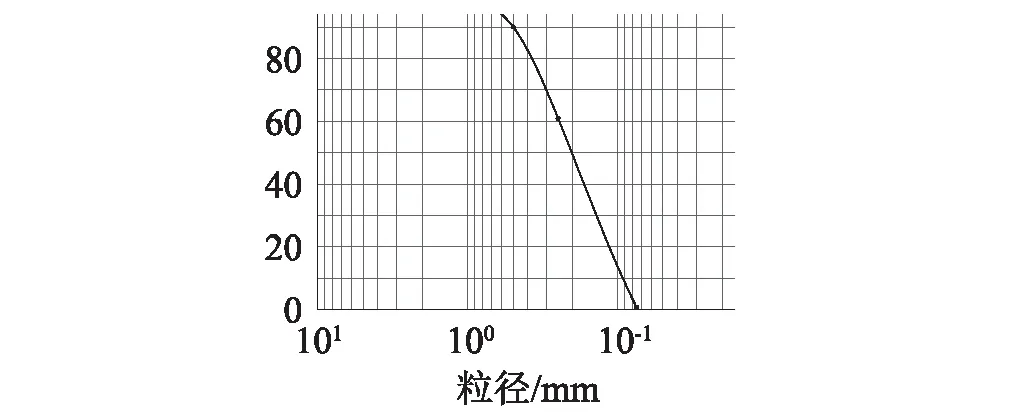
圖4 試驗用土粒徑曲線Fig.4 The particle size of soil

圖5 土-結構相互作用模型Fig. 5 The soil-structure interaction model

圖6 樓層平面圖Fig.6 The plane graph of floor

2.2 模型簡化方法可靠性驗證

采用大型有限元軟件ANSYS建立了兩個數值模型：原型結構和簡化后的試驗模型。通過對比兩個數值模型的固有振型、固有周期，以及不同峰值加速度下的最大層間位移和最大層間位移角來驗證該簡化方法的可靠性。

圖7給出了兩個數值模型的振型計算結果。由圖7可知，兩數值模型前5階振型一致；前2階振型分別為沿Y軸和X軸方向的平擺；第三振型為扭轉振型；第4、第5階振型分別為沿Y軸和X軸方向具有一個反彎點的擺動。將兩個模型的固有周期、最大層間位移和最大層間位移角進行對比，統計結果分別如表3～表5所示。固有周期最大誤差為2.6%，層間位移的最大誤差為5.42%，層間位移角的最大誤差為8.56%。簡化模型與原型結構的固有特性和動力反應較為接近，滿足振動臺試驗精度的要求。因此，該簡化方法是合理的，簡化后的試驗模型可作為試驗的研究對象。

圖7 振型圖對比Fig.7 Comparison on the model shape

振型第1階第2階第3階第4階誤差/%2.31.92.61.8

表4 層間位移的誤差

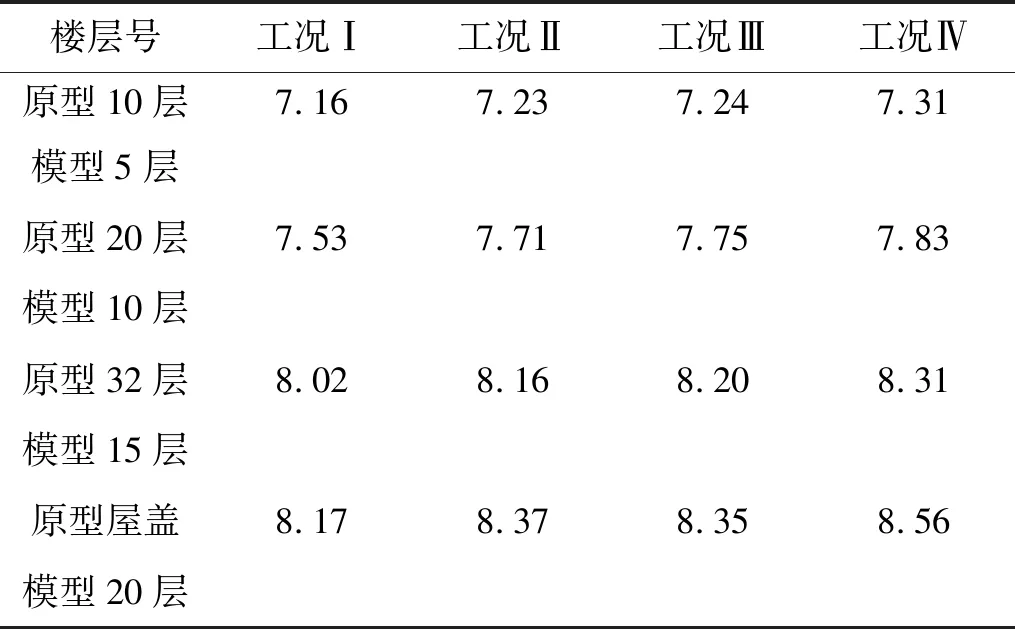
表5 層間位移角的誤差

2.3 測點布置

為獲得上部結構在多向地震作用下的動力反應，兩種模型上部結構沿高度方向均勻布置了27個加速度計。由于上部結構相同，兩種試驗模型的測點布置一致，加速度測點布置如圖8所示。

圖8 測點布置示意圖Fig.8 The sketch of the arrangement of gauges

2.4 加載工況

振動臺的設備性能是影響試驗成功與否的重要因素。本次試驗采用同濟大學引進的MTS模擬地震振動臺，該振動臺采用電液伺服驅動方式，具備三向六自由度試驗能力，集臺面編程、迭代補償、數據分析和處理以及管理等功能于一體。最大承載重量25 t，最大驅動加速度為1.2g，能夠模擬簡諧振動、沖擊以及地震作用，該振動臺設備性能能夠滿足本試驗的需求。

試驗選用兩條天然地震波(El Centro波和Kobe波)以及一條上海人工波作為振動激勵。由原型結構與試驗模型的加速度相似比例Sa=3.8可得，在模擬7度、8度和9度工程場地地震作用時，輸入振動臺的地震波峰值加速度應分別調整為0.38g，0.76g和1.14g。FB和SSI兩個試驗模型的加載工況完全相同，試驗加載工況詳如表6所示。

表6 加載工況

2.5 破壞現象

試驗模型經歷了加速度峰值從0.38～1.14g不斷增大的過程，結構破壞現象簡述如下：

(1)7度罕遇水平地震作用后，FB模型無損傷發生，SSI模型上部結構中部的外框架角柱發生寬度約為1 mm的水平裂縫，核心筒和群樁基礎均未出現明顯裂縫。

(2)8度罕遇水平地震作用后，FB試驗模型的外框架柱底部發生寬度為1 mm的水平裂縫，核心筒無破壞現象；SSI試驗模型的群樁樁身出現約為1 mm的水平細微裂縫(見圖9)，上部結構中部的外框架柱水平裂縫未發生明顯擴大。

(3)9度罕遇水平地震作用后，FB試驗模型的外框架柱底部水平裂縫繼續延伸，同時，核心筒出現寬度約為1 mm的水平裂縫(見圖10)；SSI試驗模型的裂縫無擴大趨勢，受損情況與8度罕遇地震作用結果基本一致。

圖9 樁基的破壞Fig.9 The failure in piles

圖10 框架柱與核心筒的破壞Fig.10 The failure in frame column and core tube

3 試驗數據處理與分析

3.1 分解信號波形分析

采用MATLAB軟件中Daubechies 15小波函數對FB和SSI兩個試驗模型的加速度采樣信號進行小波包2層分解[13-14]。由于各工況采樣信號的小波包分解結果均呈現相似的趨勢結果，鑒于篇幅有限，僅給出9度罕遇El Centrol波作用下FB和SSI試驗模型結構頂部沿X軸方向采樣信號的分解結果(見圖11)。

圖11 FB和SSI模型采樣信號分解Fig.11 Sampling signal decomposition of the FB and SSI models

由圖11可知，相比FB模型采樣信號的分解波，SSI模型分解波的加速度峰值明顯較小，這是土對振動能量的耗散使得SSI上部結構振動能量減小的結果。高次分解波的波形呈現為逐漸衰減的“拍”波形式，其峰值加速度量級極為微小，且1次波的小波包系數和頻帶能量(見圖12)均接近于1，說明高次分解波均為隨機噪聲波。因此，試驗模型的振動主要由1次波控制，將采樣信號進行2層小波包分解是合理的。

圖13給出了在9度罕遇El Centrol波作用下，FB和SSI兩個試驗模型不同樓層的總能量歸一化比例結果。SSI模型各樓層總能量之和為0.044 J，遠大于FB模型各樓層總能量之和0.006 J。FB模型各樓層的總能量隨樓層高度的增大而增大，而SSI模型各樓層的總能量隨樓層高度的增大呈現先減小后增大的趨勢。上述現象表明，相比FB模型，SSI模型的土耗散了6/7的地震能量，從而使得上部結構所吸收的能量以及振動強度大幅減小。同時，SSI模型改變了能量沿樓層高度的分布。

圖14給出了在9度罕遇El Centrol波作用下，FB和SSI兩個試驗模型不同樓層的加速度1次分解波。通過對比可知，SSI試驗模型第1層～第3層的峰值加速度略大于FB模型，其它樓層的的峰值加速度則明顯小于FB模型；FB模型的峰值加速度隨樓層高度的增大而增大，SSI模型的峰值加速度隨樓層高度的增大呈現為先減小后增大的趨勢。上述現象表明，土對結構的動力響應有減小的趨勢，但結構沿高度方向動力響應變化的趨勢卻與剛性基礎有明顯差別。

圖12 分解波能量Fig.12 The energy of decomposition wave

圖13 不同樓層總能量對比Fig.13 Comparison on the total energy of different floors

3.2 分解信號頻譜分析

采用等能量的白噪聲對兩個試驗模型進行掃頻，從而獲取模型在地震作用下固有特性的變化[15-16]。FB和SSI模型各測點白噪聲1次分解波的頻譜區間、主頻率、主頻率變壞百分比以及小波包系數統計結果，如表7所示。

由表7可知，兩試驗模型在各工況下的小波包系數接近于1，表明兩個試驗模型在地震激勵下主要呈現為基頻振動。為受損前FB模型的基頻為7.12 Hz遠大于SSI模型的基頻3.28 Hz，表明考慮地基土的能夠降低結構振動的基頻。隨著地震烈度的增大，兩試驗模型的上部結構基頻均呈現降低的趨勢，表明結構在地震作用下不斷發生破壞。9度罕遇地震作用下FB模型的基頻降低39.61%，而SSI模型的基頻僅降低14.02%，表明通過地基土的地震能量耗散，SSI模型上部結構的破壞明顯小于FB模型。

圖14 不同樓層1次波對比Fig.14 Comparison on the 1st wave gauged at different floors

工況1次波頻譜區間/Hz基頻/Hz基頻變化百分比/%小波包系數WN1-FB0～12.07.1200.999 917WN2-FB0～12.06.3311.100.999 920WN3-FB0～12.05.5122.610.999 946WN4-FB0～12.04.3039.610.999 878WN1-SSI0～12.03.2800.999 905WN2-SSI0～12.02.969.760.999 886WN3-SSI0～12.02.9111.280.999895WN4-SSI0～12.02.8214.020.999 966

3.3 能量變異最值指數分析

圖15和圖16分別給出了不同烈度地震作用下FB和SSI試驗模型不同樓層的能量變異最大值指數(Maximum Energy Variation Index, MEVI )[17-18]。由圖15可知，FB模型不同樓層的MEVI隨地震烈度的增大而增大，8度罕遇地震作用后MEVI增幅最大，沿樓層高度方向的結構底部MEVI最大。表明FB模型在地震作用下上部結構受損程度隨地震烈度的增大而增大，結構受到8度罕遇地震作用后損傷變化最為明顯，沿樓層高度方向上部結構底部的最易發生損傷。

由圖16可知，SSI模型不同樓層的MEVI隨地震烈度的增大并未產生明顯的變化，沿樓層高度方向結構中部的MEVI顯著大于其它各樓層。表明SSI模型在地震作用下，沿樓層高度方向的結構中部受損最為嚴重，上述分析結果與試驗現象也是相吻合的。

圖15 FB模型能量變異最值指數Fig.15 The maximum energy variation index of the FB model

圖16 SSI模型能量變異最值指數Fig.16 The maximum energy variation index of the SSI model

4 結 論

本文采用振動臺試驗的方法從小波包能量的角度研究了土對高層框筒結構震動響應的影響。通過對比FB和SSI兩種試驗模型在不同烈度地震作用下上部結構的能量分布、振動基頻變化以及易損傷部位的差別得到以下結論：

(1) 在地震作用下，經土體的能量耗散SSI體系上部結構的峰值加速度、振動基頻以及所吸收的能量相比FB體系顯著降低。

(2) FB體系上部結構所吸收的地震能量隨樓層高度的增大而增大，而SSI體系則隨樓層高度的增大呈現先減小后增大的趨勢。

(3) FB體系的損傷程度隨地震烈度的增大而增大，上部結構的底部最易發生損傷；SSI體系的損傷程度隨地震烈度的增大不明顯變化，上部結構的中部最易發生損傷。