柱塞泵壓力脈動隨機動力特性分析及實驗研究

顧振杰， 白長青

(西安交通大學 航天航空學院 機械結構強度與振動國家重點實驗室，西安 710049)

柱塞泵具有良好的自吸性能及較強的介質適應性，常被作為各領域管道輸運工程中的動力源。泵容積的周期性變化，會使管道內流體的壓力出現脈動特性。由于流固耦合作用，管路系統中的壓力脈動會引起管道結構振動，嚴重時可以導致機器故障或管道破裂，嚴重影響正常生產和工作人員安全。

為了防止柱塞泵壓力脈動對管路系統的破壞，國內外學者分別從柱塞泵本身及管道系統兩方面進行了研究并取得了一定進展。柱塞泵由于流量脈動而引起壓力脈動，在理論分析上，朱俊華等[1]對柱塞泵的流量脈動機理進行了詳細的描述，俞繼印等[2]和葉敏[3]則分別提出了流量脈動的簡化公式和修正公式。在數值模擬上，張天霄[4]建立了液壓柱塞泵壓力脈動的仿真函數模型；徐兵等[5]基于虛擬樣機研究了油液黏度、體積彈性模量對柱塞泵出口壓力脈動特性的影響；Edge等[6]提出了增加阻尼槽中流體加速度運動慣性的模型，并分析了配流盤和泄槽設計對缸壓和泵流量脈動的影響；Meincke等[7]則通過考慮油液的彈性和氣穴模型對多柱塞泵進行了動態建模。對管道系統內壓力脈動問題，周紅等[8]運用運動方程與連續方程對壓力脈動進行了建模；王秋穎[9]用波動方程求解了壓力脈動表達式；劉偉等[10]采用首次超越破壞和疲勞累積破壞準則對液壓管路可靠度進行了仿真,并得到了泵源脈動幅值對管路系統可靠性的影響。考慮實際管道復雜性，薛瑋飛等[11-12]用有限元方法分析了管路系統的氣柱固有頻率。為了消減壓力脈動作用，李永東等[13-15]還針對壓力脈動問題設計了衰減器，以達到從流體角度實現管道振動控制的目的。目前，對柱塞泵及壓力脈動問題的研究多是從確定性角度進行的，而隨著工業和科技的發展，柱塞泵更多地被應用于高精密、高壓力、高流速的工程領域，流體流動、轉子轉動等隨機性引起的壓力脈動波動特性對輸流管道的安全性和可靠性影響也更加顯著。在柱塞泵壓力脈動隨機動力特性的研究中，除了文獻[16]分析了制造誤差對曲柄柱塞泵流量脈動的影響外，柱塞泵壓力脈動隨機性問題并沒有得到足夠的重視。

目前，對于柱塞泵壓力脈動隨機動力特性的分析較少，壓力脈動隨機分布形式尚不明確。因此，本文建立了柱塞泵壓力脈動隨機動力學表達式，并通過對三柱塞泵系統進行實驗得到了壓力脈動隨機參數的分布規律。在實驗的基礎上采用有限元方法建立管道動力學模型，并將模擬結果與實驗進行了對比驗證。

1 柱塞泵壓力脈動隨機動力學表達式

在實際工程應用中，由于流體流動、轉子轉動隨機性等因素會造成多柱塞泵中每個柱塞的排液量存在差異，進而引起泵管路中的壓力脈動存在隨機性。

如圖1所示，對于某一柱塞，設ω，R，β，L分別為曲柄轉角速度、曲柄長度、連桿旋轉角度和連桿長度。則曲柄旋轉角度φ、連桿比λ分別為φ=ωt，λ=R/L，其中t為時間。根據曲柄連桿運動規律計算得到活塞的位移x=Rcosφ+Lcosβ-R-L，可得由容積變化引起的柱塞瞬時輸出壓力p為

(1)

式中：μi為影響壓力脈動的隨機參數；A為柱塞面積；f(Zs,Ze)[17]為與柱塞自身阻抗Zs和管路外阻抗Ze相關的函數，可通過實驗或數值分析確定。對于第i個柱塞，隨機參數μi可以寫為

(2)

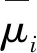
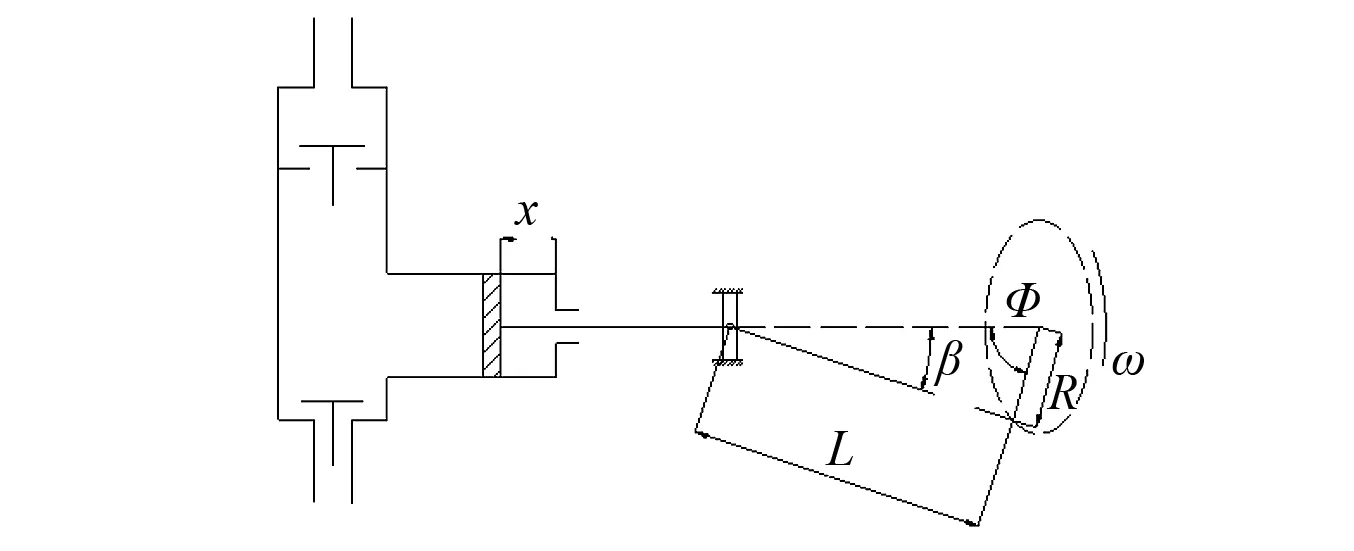
圖1 柱塞曲柄連桿工作示意圖Fig.1 Structure of plunger crank connecting rod

對于多柱塞單作用泵，曲柄轉動一圈(φ=2π)，單個柱塞完成一個完整的工作周期，吸排液各一次。設多柱塞泵瞬時輸出壓力為P，則可得描述多柱塞泵輸出壓力的隨機動力學表達式

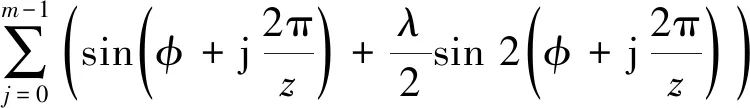
(3)

式中：z為泵柱塞數；m為處于排液過程中的柱塞數。當泵柱塞數為偶數時，m=z/2；為奇數時，m=(z±1)/2。

從式(3)可知，壓力脈動隨機特性由參數μi確定，其概率分布特性是壓力脈動隨機特性分析的關鍵。為了得到μi的概率分布規律，本文搭建了如圖2所示的實驗平臺，并進行隨機壓力脈動實驗。該實驗系統主要由三柱塞往復泵，與其相連的管道系統，壓力傳感器，激光位移傳感器，Daqbook/2000A數據采集系統及供電電源組成。實驗流程如圖3所示：在泵出口部位及管道彎頭處分別設置壓力傳感器和激光位移傳感器，測量所得到的壓力信號和位移信號由傳感器采集并轉化為電信號后進入數據采集系統。所得數據經預處理后輸出，并用Matlab對實驗數據進行統計分析。

圖2 三柱塞泵管道系統Fig.2 Three plunger pump-pipe system

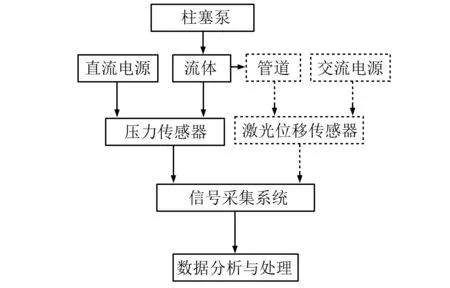
圖3 實驗流程圖Fig.3 Experimental flow chart

泵工作過程中，每間隔一定時間對管道壓力及位移進行采樣，并對樣本(200組)進行頻域分析。泵轉速為n=360 r/min時, 實驗測得18.44 Hz為壓力脈動基頻。該頻率所對應幅值及波動幅度最大，對管路系統影響也最為顯著，故選取該頻率對應的壓力脈動幅值進行統計。經過統計得到壓力脈動均值及標準差分別為1.697×104Pa，5.558×103Pa，統計分析散點圖及直方圖如圖4所示。對直方圖進行擬合發現，壓力脈動幅值服從極值I型分布，概率密度分布函數為

f(x)=αe[-α(x-k)-e-α(x-k)]

(4)

式中：α=1.282 5/σX，σX為標準差；k=mX-0.577 2/α，mX為均值。

圖4 壓力脈動散點圖及直方圖Fig.4 Scatter plot and histogram of pressure fluctuation

2 壓力脈動及管道位移響應隨機動力特性分析

2.1 壓力脈動隨機動力特性分析

不考慮隨機因素影響時(μi=0)，隨機壓力脈動表達式退化為確定性表達式。當三柱塞單作用泵轉速為n=360 r/min時，得到壓力脈動時域波形如圖5所示。從圖5的實驗結果可知，所測得的壓力(已減均值)具有明顯脈動特性，且壓力脈動峰-峰值為隨機波動量。對比隨機及確定壓力脈動波形發現， 隨機性壓力脈動較確定性壓力脈動能夠體現出實驗壓力脈動測量中表現出的顯著隨機波動特性，說明隨機壓力脈動表達式更符合實際工況。

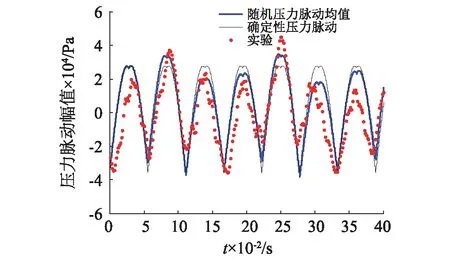
圖5 壓力脈動時域波形Fig.5 Time domain waveforms of pressure fluctuation

對壓力脈動進行頻域分析，得到隨機、確定及實驗壓力脈動幅值的頻譜對比結果，如圖6所示。從圖6可知，隨機及確定性壓力脈動最高幅值對應頻率為18 Hz，與實驗結果18.44 Hz相符。由于隨機因素影響，隨機模型頻率特性中出現1/3倍頻(6 Hz)，合理解釋了實驗結果中出現1/3倍頻(6.14 Hz)的現象。

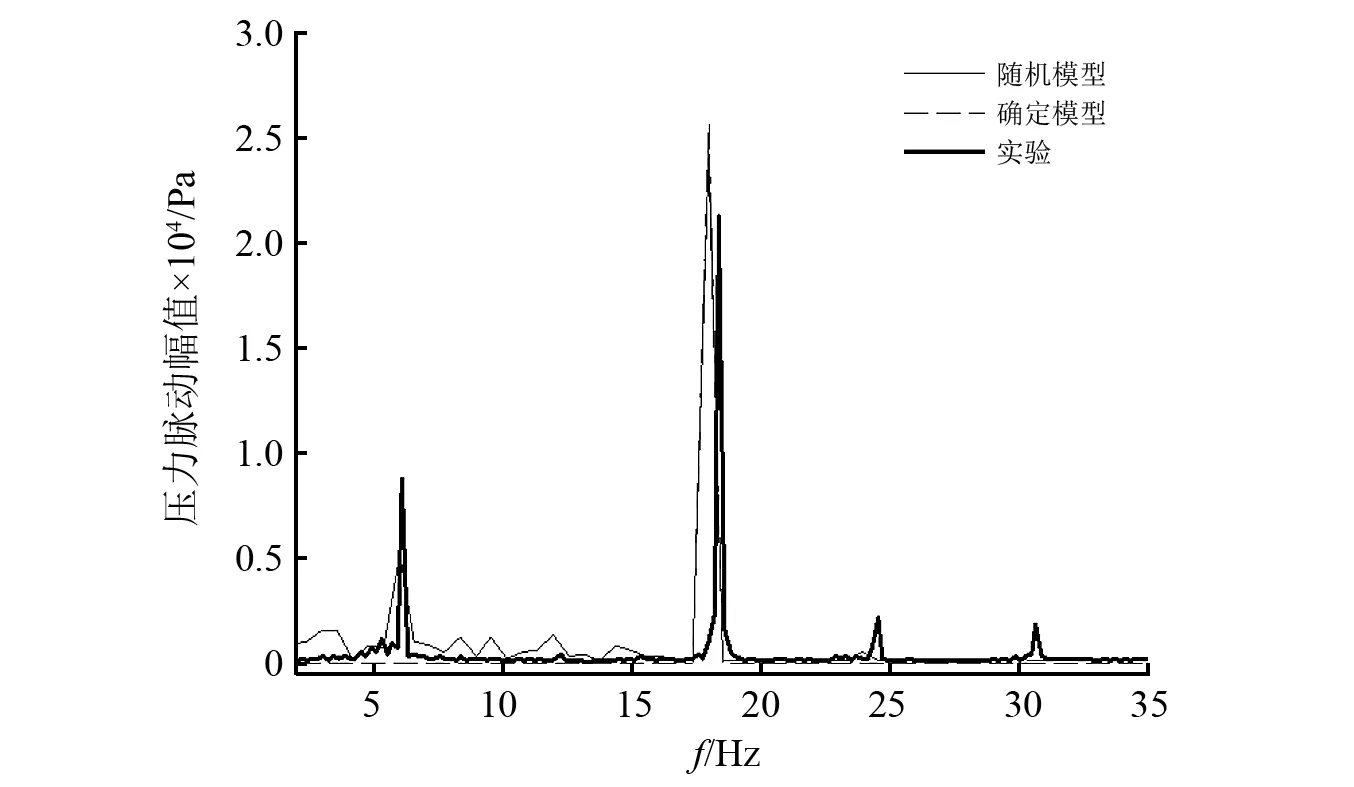
圖6 壓力脈動頻域圖Fig.6 Frequency domain diagram of pressure fluctuation

2.2 管道位移響應分析

對實驗測得的位移響應進行統計分析，處理過程同壓力脈動分析。得到位移響應最高幅值對應頻率為18.44 Hz(與壓力脈動頻率特性相同)，且均值及標準差分別為5.785×10-5m，2.026×10-5m。針對實驗室柱塞泵出口管路，建立管道系統為77個有限單元和78個節點的動力學模型。按照所給隨機壓力脈動表達式，應用蒙特-卡羅方法將隨機壓力脈動引入所建模型，并采用逐步時間積分方法編程求得彎頭位置位移響應。對計算數據進行統計分析并與實驗結果對比，如圖7及表1所示。從圖7可知，位移響應也服從極值I型分布，且數值分析及實驗吻合良好。位移響應均值和標準差誤差均在12%以內(見表1)，證明所給表達式能夠準確模擬柱塞泵輸流管道內壓力脈動的隨機動力特性。

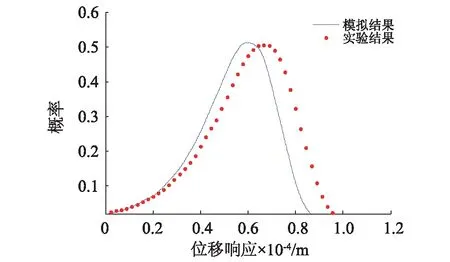
圖7 位移響應概率對比曲線Fig.7 Comparison for numerical and experimental probability distribution of displacement response

位移響應均值標準差實驗/m 5.785×10-52.026×10-5數值模擬/m5.267×10-51.793×10-5誤差/%8.9511.5

3 結 論

本文考慮隨機因素影響，提出了柱塞泵壓力脈動隨機動力學表達式。通過對三柱塞泵輸流管道系統進行實驗，驗證了表達式的合理性并得到了壓力脈動隨機參數的概率分布規律。基于實驗建立了管道系統的動力學有限元模型，并將數值計算結果與實驗測得位移響應進行了對比。通過以上分析，得到以下結論：

(1)實驗統計分析發現，隨機壓力脈動與位移響應頻率特性相同且幅值均服從極值I型分布。

(2)由于隨機因素影響，壓力脈動幅值在一定范圍內波動且頻率特性中出現1/3倍頻，與實驗結果相符。

(3)實驗及數值計算所得位移響應的均值和標準差誤差分別為8.95%，11.5%，證明應用所給表達式模擬柱塞泵管道系統內壓力脈動隨機動力特性是合理可行的。