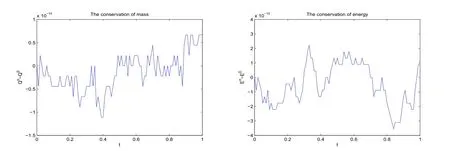
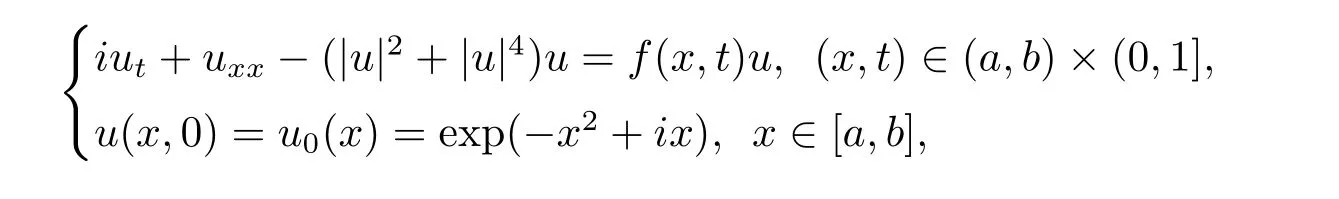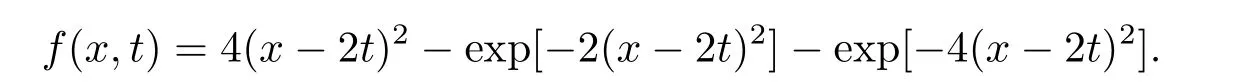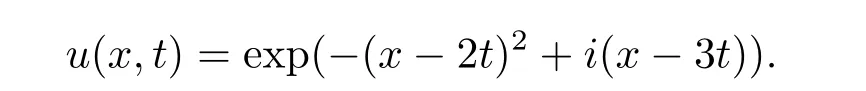五次非線性Schr?dinger 方程的一個新型守恒緊致差分格式
薛 翔,王廷春
(南京信息工程大學數學與統計學院,江蘇南京210044)
1 引言
非線性Schr?dinger 方程在量子力學、非線性光學等物理領域有著非常廣泛的應用.本文研究如下一類五次非線性Schr?dinger 方程的初邊值問題[1]
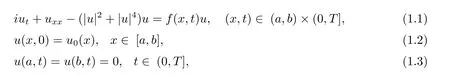
其中f(x,t)為實值函數,u(x,t)為復值函數,u0為已知的復值函數.不難驗證,當f(x,t)≡f(x)時,該方程滿足兩個重要的守恒律,即總質量和總能量守恒[1,2]
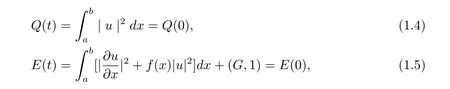
其中
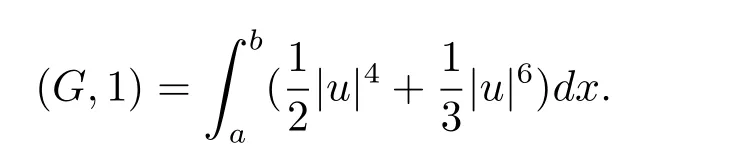
關于非線性Schr?dinger 方程的數值研究已有很多結果.Bao 等人[3?5]運用時間分裂擬譜方法對非線性Schr?dinger/Gross-Pitaeviskill 方程進行了數值求解,并對某些物理現象進行了數值模擬;Argyris 和Akrivis 等人[6?9]運用有限元法對該方程進行了數值研究;Dehghan 和Mirzaize 運用無網格法對該方程進行了數值求解[10?11].文獻[12–14]則運用譜方法和擬譜方法對該方程進行了數值求解和誤差分析.因編程簡單并能保持原問題的某些守恒性質,有限差分法廣泛應用于非線性Schr?dinger 方程的數值模擬[15?18].然而關于五次非線性Schr?dinger 方程的數值研究尚不多見.張魯明、常謙順等人[1?2]對該方程提出兩個二階有限差分格式,證明其保持原問題的兩個守恒性質,同時建立了L2范數下的最優誤差估計.王詢等人[19]用待定系數的方法構建了一類五點有限差分格式,該格式族在選取適當的參數后,其計算精度在空間可達四階,然而計算中在每一個時間步都需要求解一個五對角代數方程組.為提高精度,文獻[20]提出一個緊致有限差分格式,但該格式是非線性的,計算中不可避免的需要迭代,從而降低計算效率.另外,該文作者也沒有分析該格式是否在離散意義下保持原問題的兩個守恒性質.鑒于以上分析,本文旨在對問題(1.1)–(1.3)構造一個線性化緊致有限差分格式,使得新格式在離散意義下依然保持原問題的兩個守恒性質.
2 有限差分格式及其守恒律
對平面區域W=[a,b]×[0,T]進行網格剖分.取正整數J,N,時空方向上的步長分別為網格點分別為
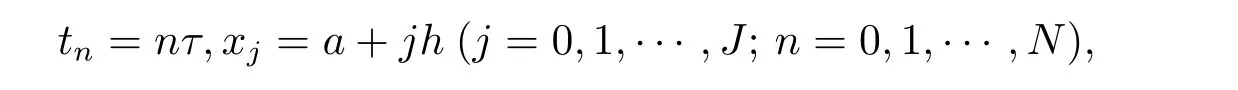
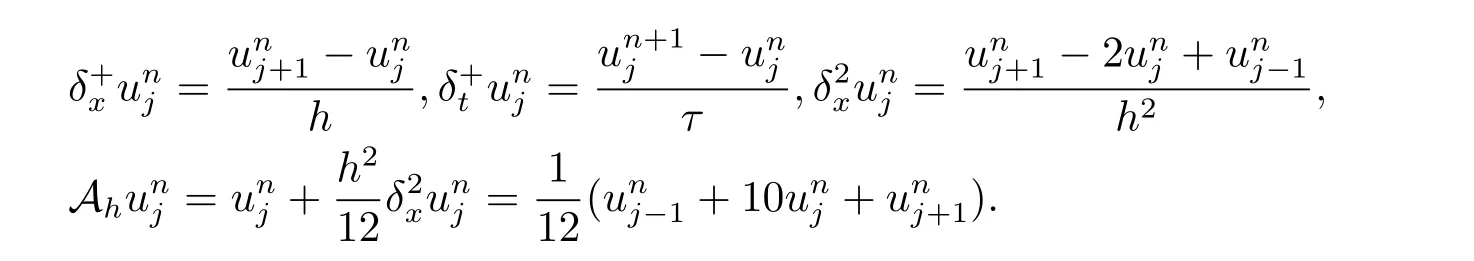
定義Xh={w|w=(ω0,ω1,···,ωJ?1,ωJ),ω0=ωJ=0}為網格函數空間.設u,v 為Xh上的任意兩個函數,其內積和范數定義為
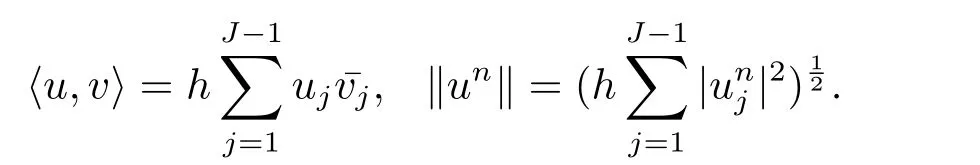
本文需要用到如下引理.
引理1[21]對于任意一個網格函數u ∈Xh,有
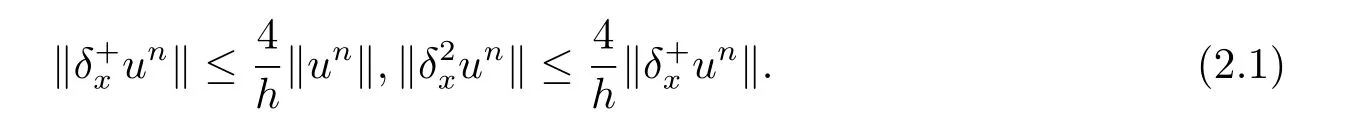
引理2[22]如果網格函數u ∈Xh,則
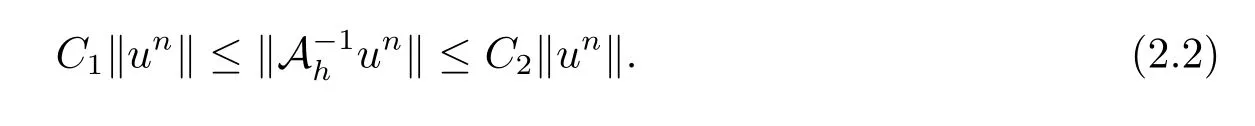
引理3[21]任給網格函數u ∈Xh,有

2.1 有限差分格式
對初邊值問題(1.1)–(1.3),本文提出如下四階緊致差分格式

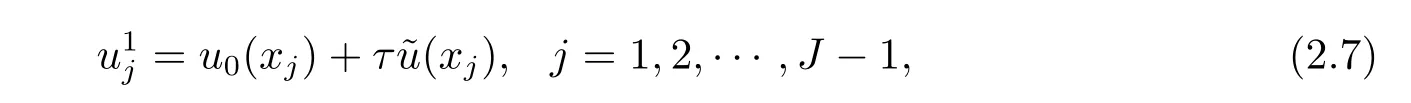
其中
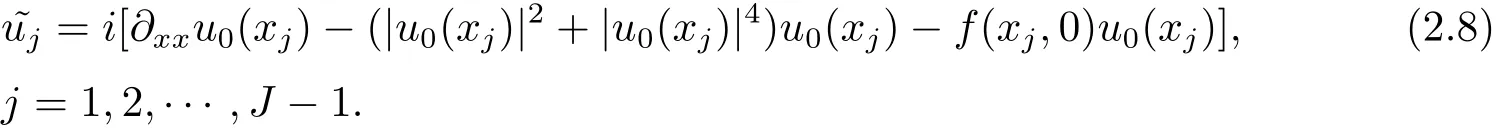
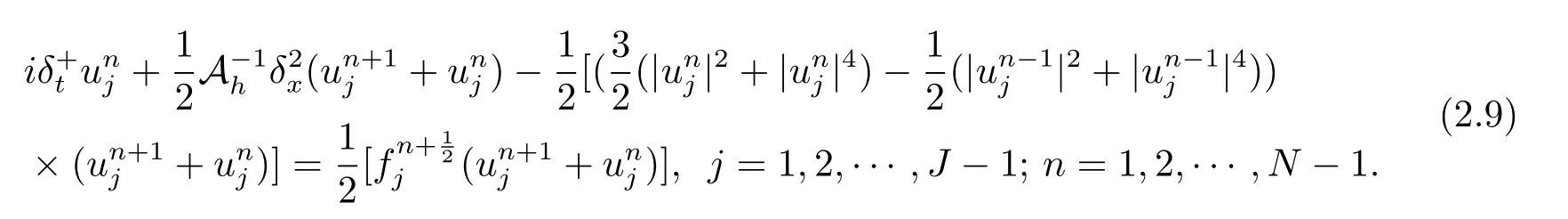
2.2 離散守恒律
為證明離散守恒律,定義
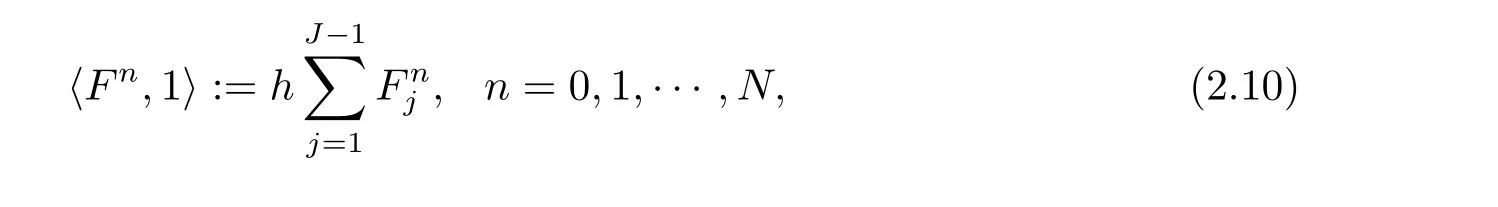
其中

n=1,2,···,N ?1,
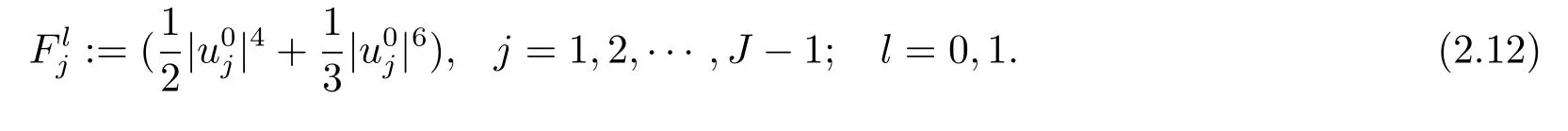
引理4(I)格式(2.4)–(2.6)在離散意義下滿足總質量守恒,即
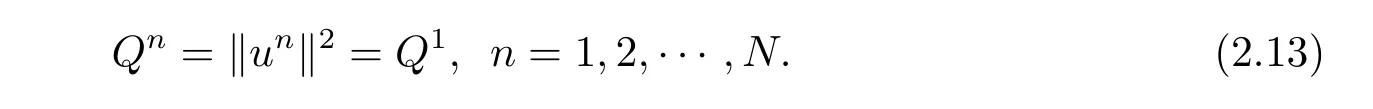
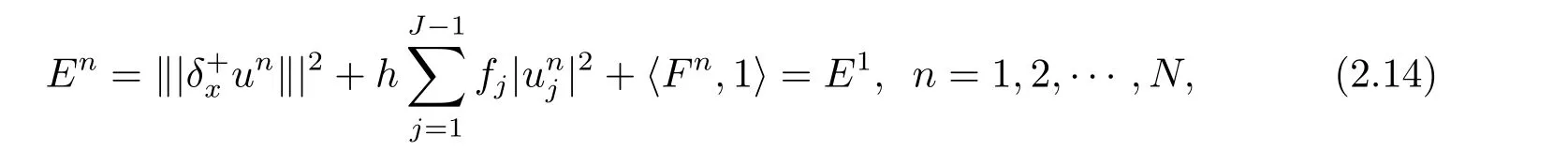
其中
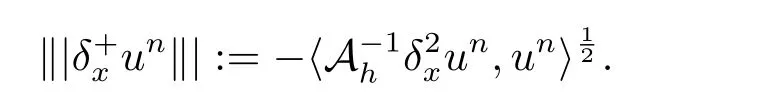
證將(2.9)式與un+1+un做內積,并取虛部得
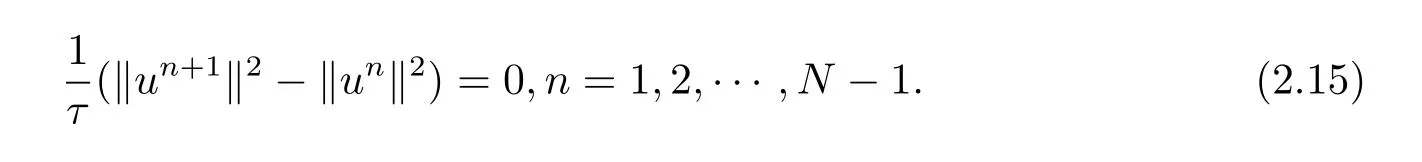
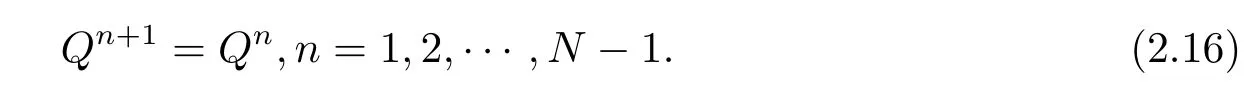
即
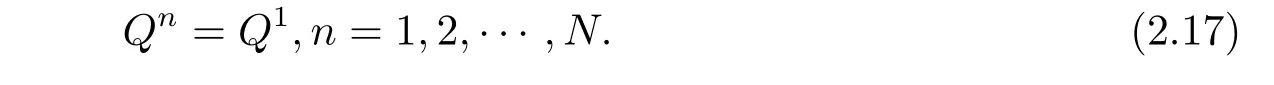
將(2.9)式與un+1?un做內積,并取實部得
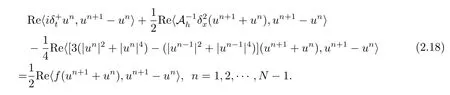
直接計算可得
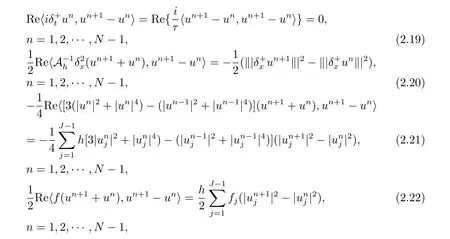
將(2.19)–(2.22)式代入(2.18)式得
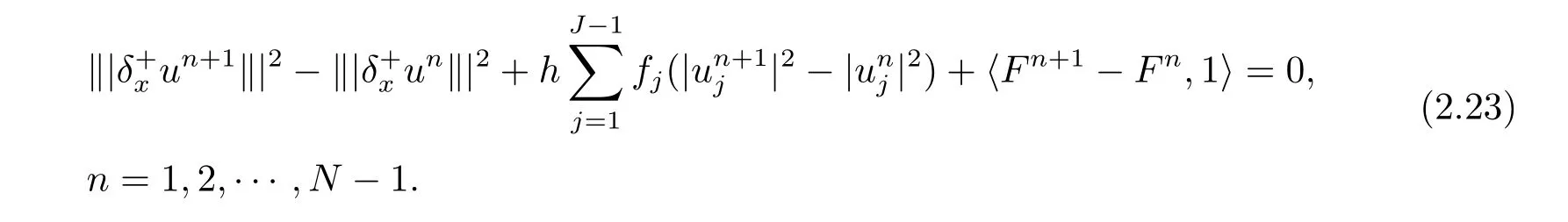
令
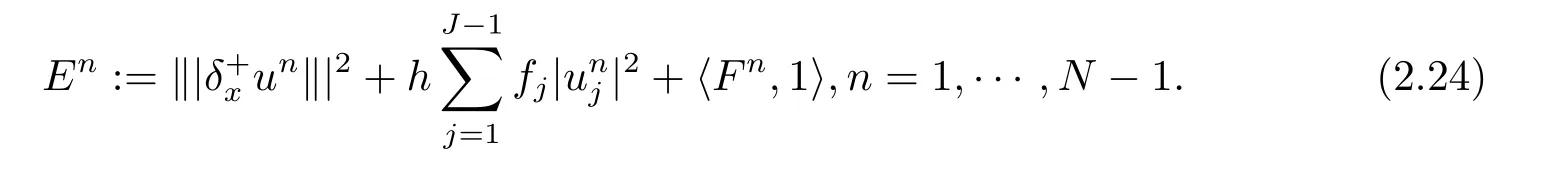
則得
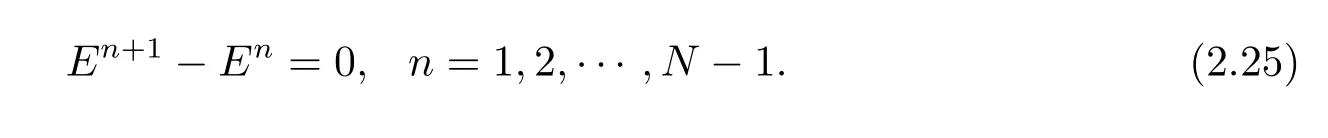
即
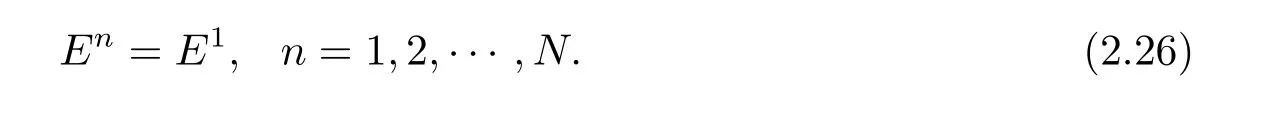
3 誤差估計
記格式(2.4)–(2.7)的局部截斷誤差為
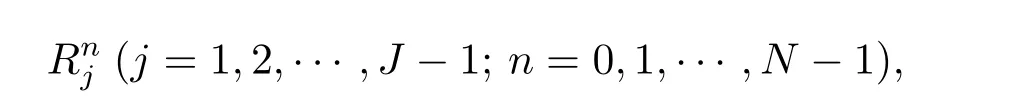
其定義如下
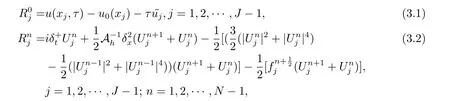
引理5格式(2.4)–(2.7)的局部截斷誤差滿足
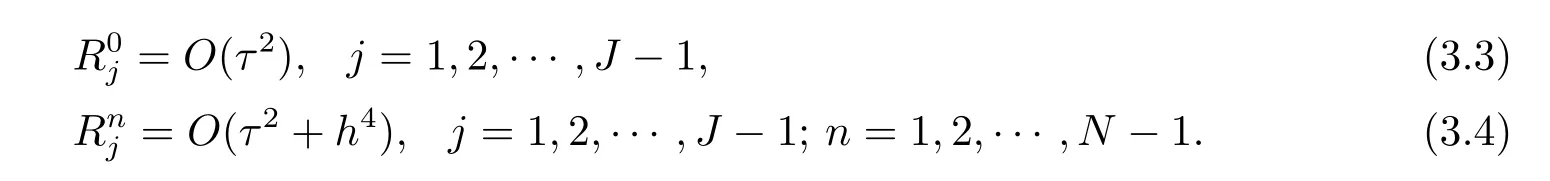
定理1假設u ∈C6,3([a,b]×[0,T]),則差分格式(2.4)–(2.7)的解以·范數收斂到初邊值問題(1.1)–(1.3)的解,收斂階為O(τ2+h4).
證將(3.1)式和(3.2)式分別與(2.7)式和(2.9)式相減可得如下誤差方程
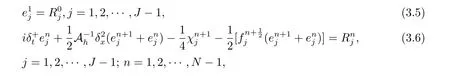
其中
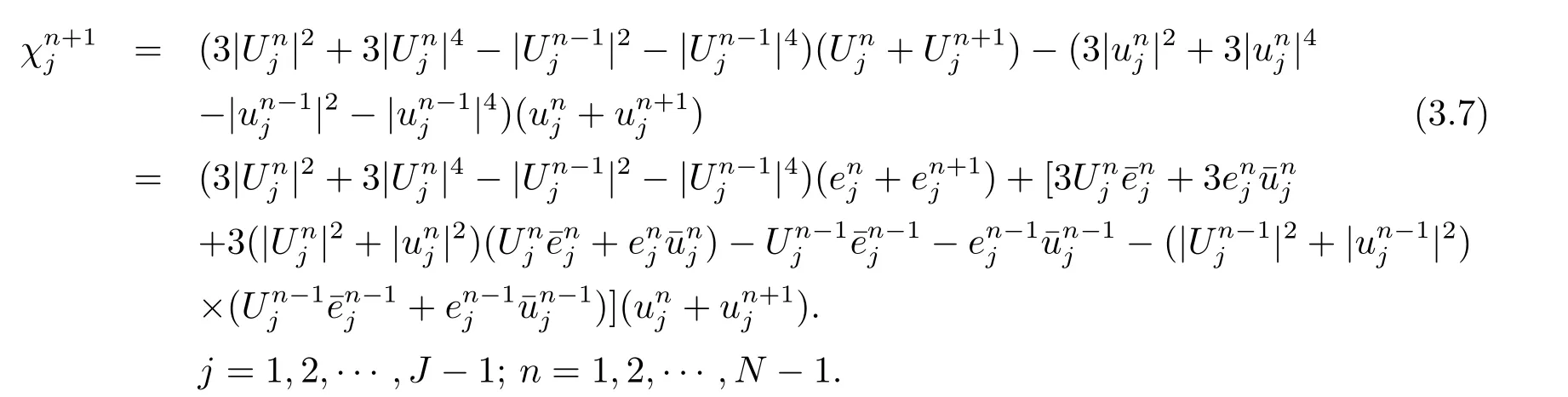
由(3.5)式和引理5 顯見

運用Taylor 展開,可得

因此有
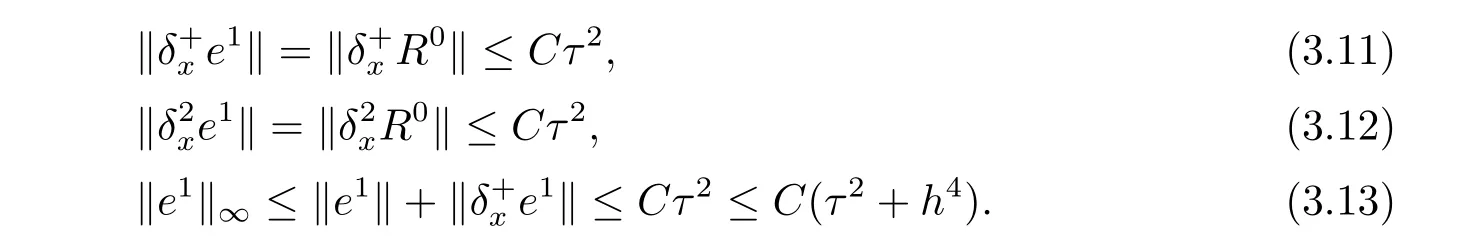
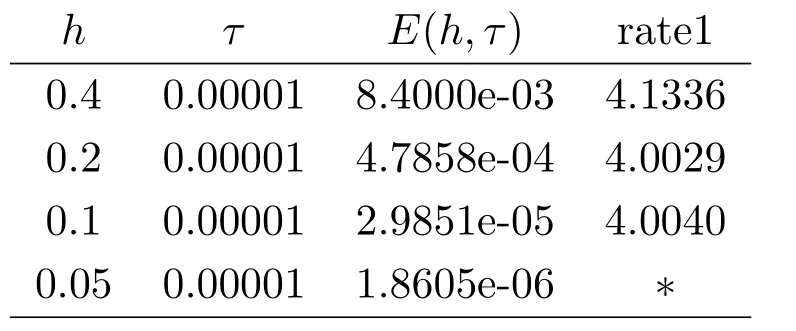
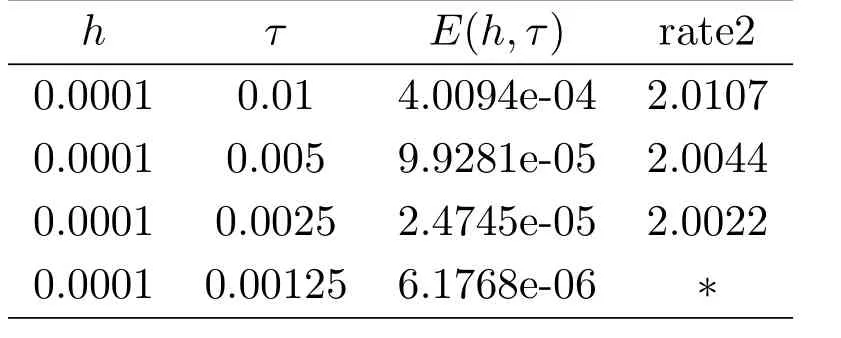
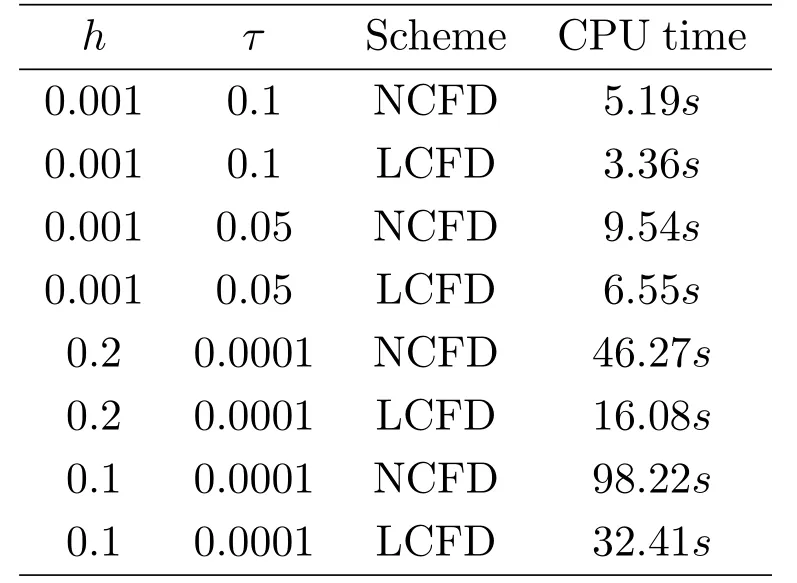
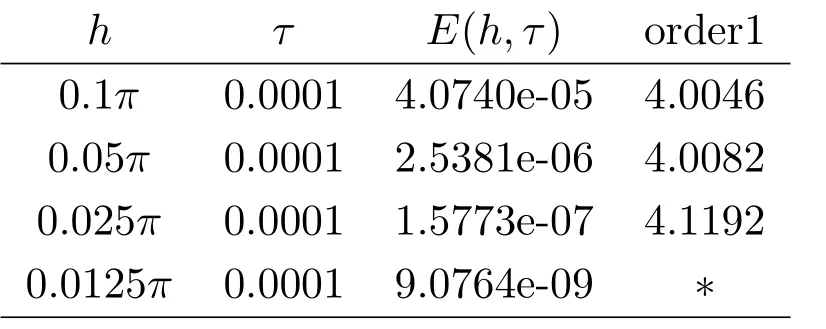
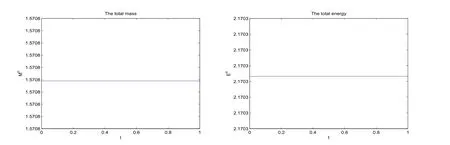
現假設當n ≤k(1 ≤k 進而可得 將(3.6)式與en+en+1做內積,取虛部得 又 由(3.18)–(3.21)式,得 上式對n 求和,有 當τ 足夠小時,由Gronwall 不等式得 由(3.6)式可得 運用引理2 有 上式對n 求和得 另外由引理1 可得 由此可見,當τ ≤h 時,有τ2/h2≤1,得 所以無論網格比如何,總有 由(3.24)式和(3.30)式可知假設(3.14)式對n=k+1 時也成立.證畢. 便于驗證格式的精度,引入以下記號 算例4.1考慮如下初邊值問題 其中 該問題的精確解為 由上式可見當x 趨向于無窮大時,u(x,t)迅速趨于0.故當?a 和b 取得足夠大時,u(a,t)和u(b,t)近似為0.因此在數值求解時取空間方向的計算區間為(?15,15),以忽略截斷誤差的影響. 在驗證空間方向(時間方向)收斂階時,取τ=0.00001(h=0.0001),這樣可以忽略時間(空間)方向的誤差影響.表1 和表2 分別給出了空間和時間方向的收斂階.在表3 中,將本文的線性格式與文獻[20]中的非線性格式做了計算效率上的比較.圖1 展示了精確解和數值解在不同時間層下的波形變化. 表1:空間方向收斂階 表2:時間方向收斂階 表3:本文中的線性格式(LCFD)與文[20]中的非線性格式(NCFD)在計算效率上的比較 圖1:算例4.1 在τ=0.01,h=0.1 時的精確解(左)和數值解(右) 算例4.2對形如iut+uxx+σ(x,t)u+(β1|u|2+β2|u|4)u=f(x,t),(x,t)∈(0,π)×(0,1].取初始值為u0(x)=sin x,則精確解為u(x,t)=eitsin x. 運用本文中的格式(2.4)–(2.6)對算例4.2 進行求解,有以下結果 表4:空間方向取不同步長時的誤差和精度 表5:時間方向取不同步長時的誤差和精度 由以上數值實驗的結果可看出:差分格式(2.4)–(2.6)在時空方向分別具有2 階和4 階精度,而且格式在離散意義下依然能夠保持總質量和總能量守恒,這完全符合定理1 和引理4的結論.除此之外,與已有格式相比,本文格式在精度相當的前提下還大幅提高了計算效率. 圖2:算例4.2 在不同時間層的總質量(左)和總能量(右) 圖3:算例4.2 在離散意義下的總質量守恒(左)和總能量守恒(右)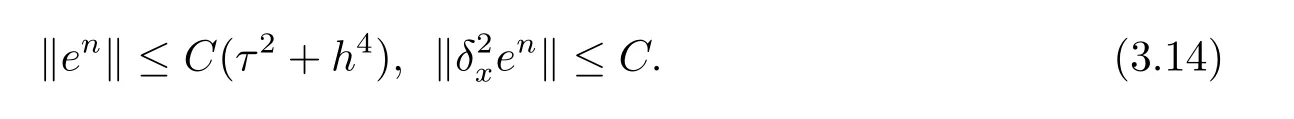

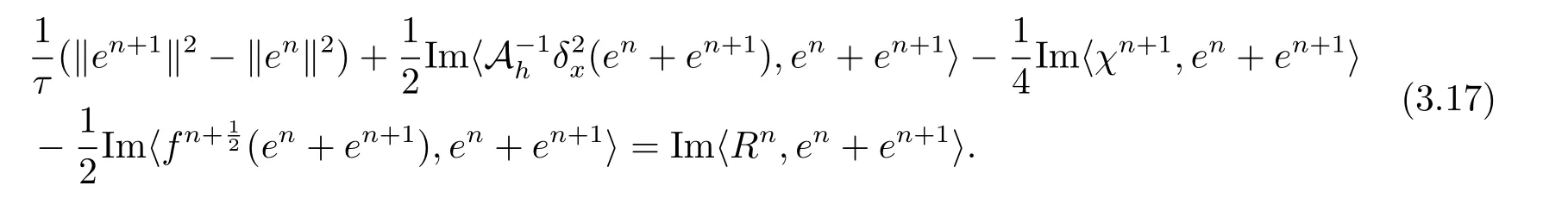
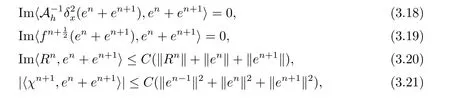

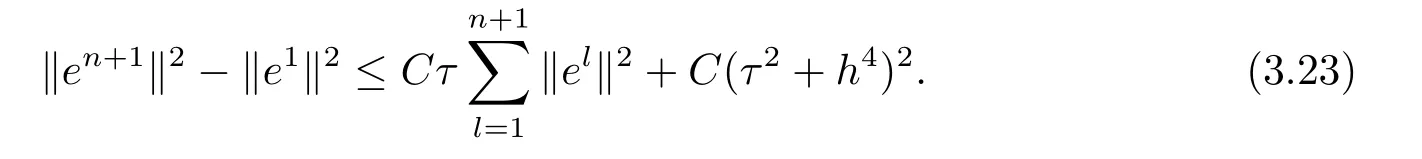

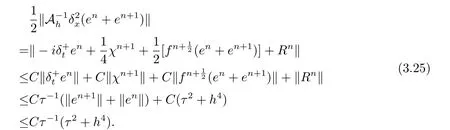
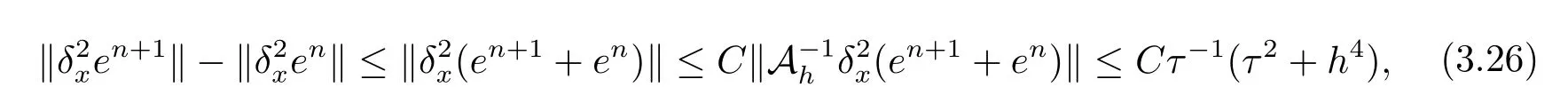
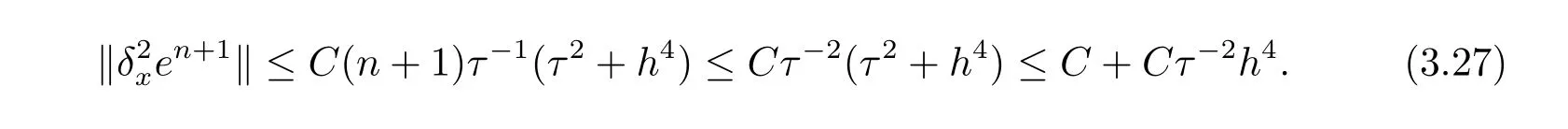

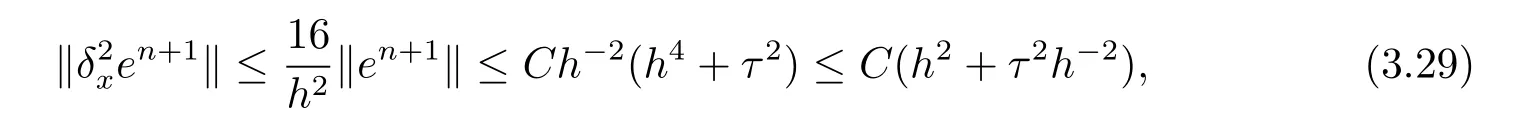

4 數值實驗