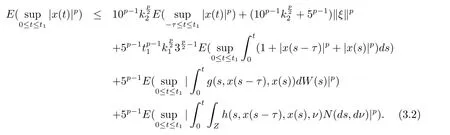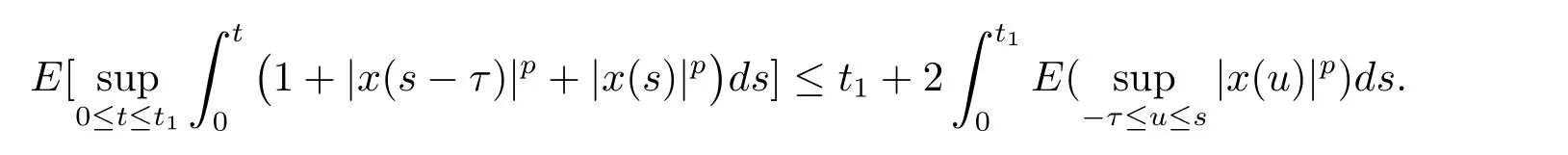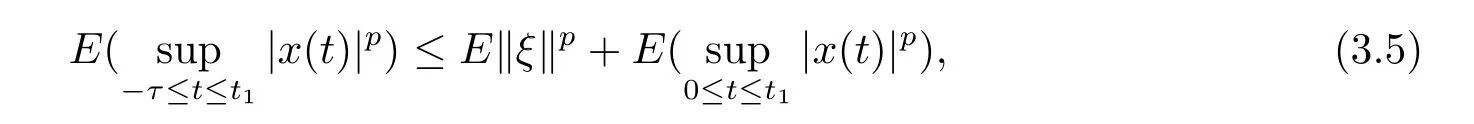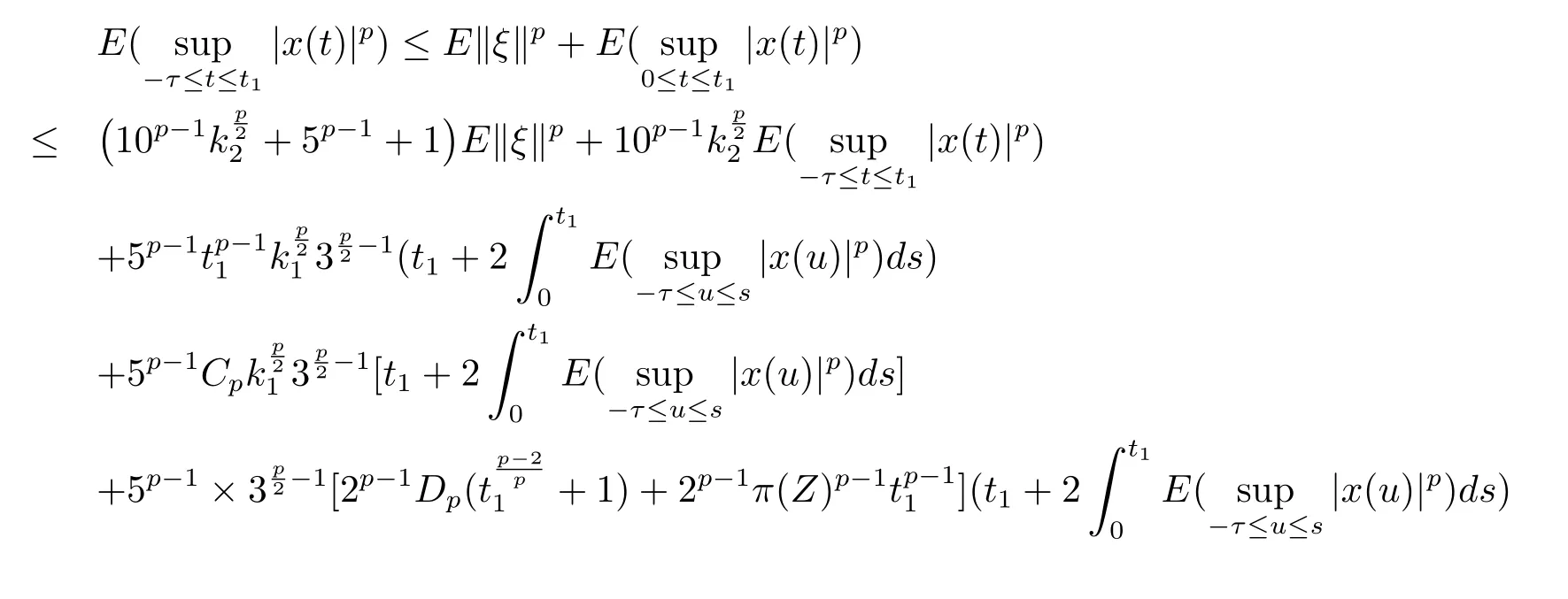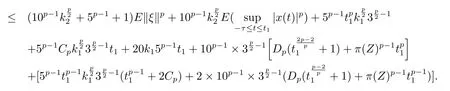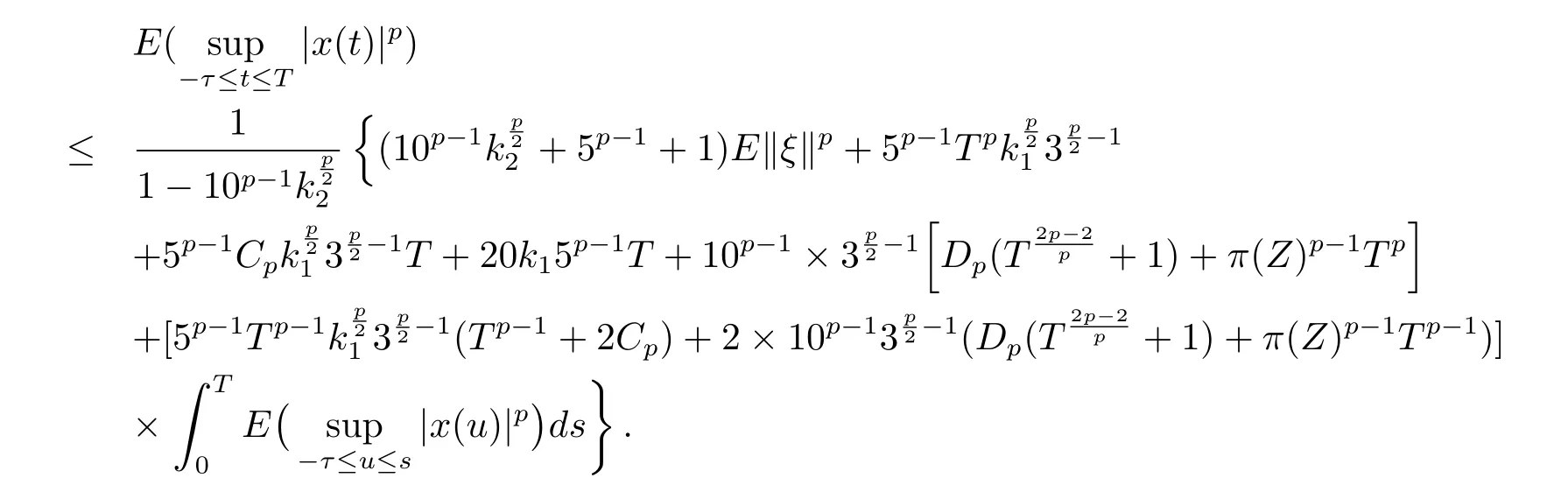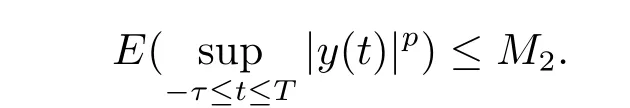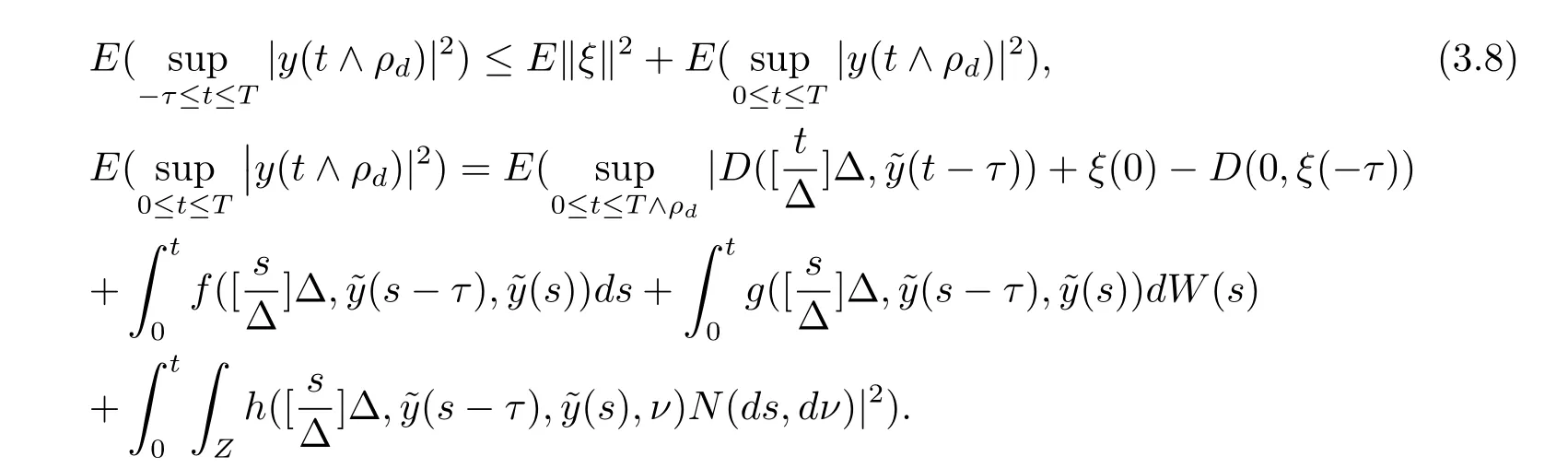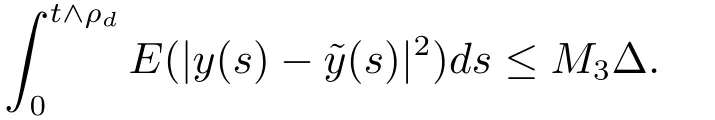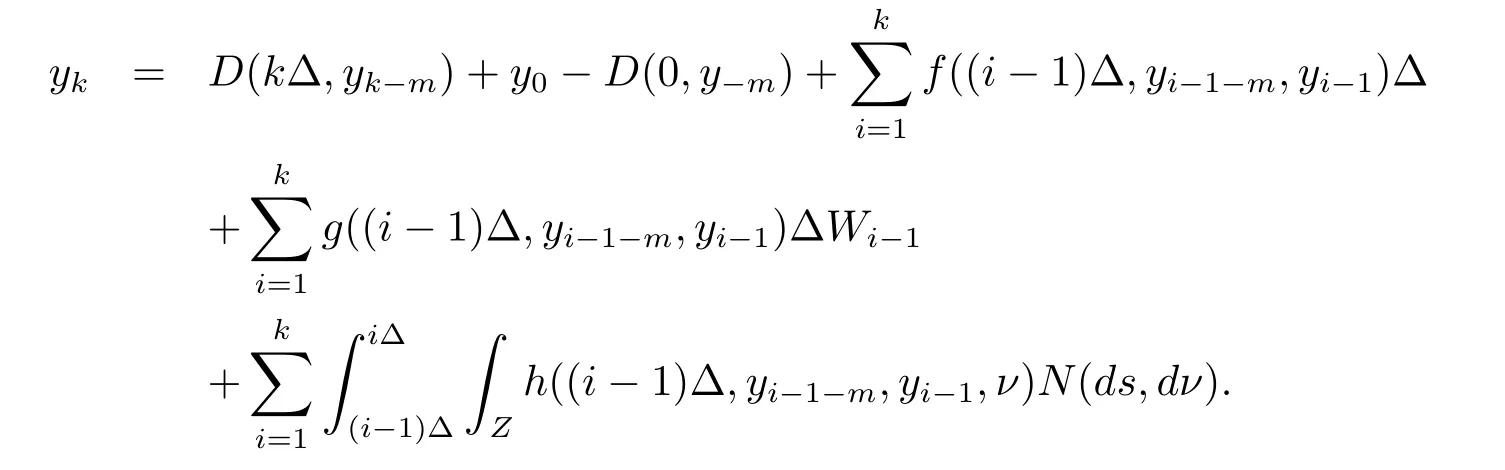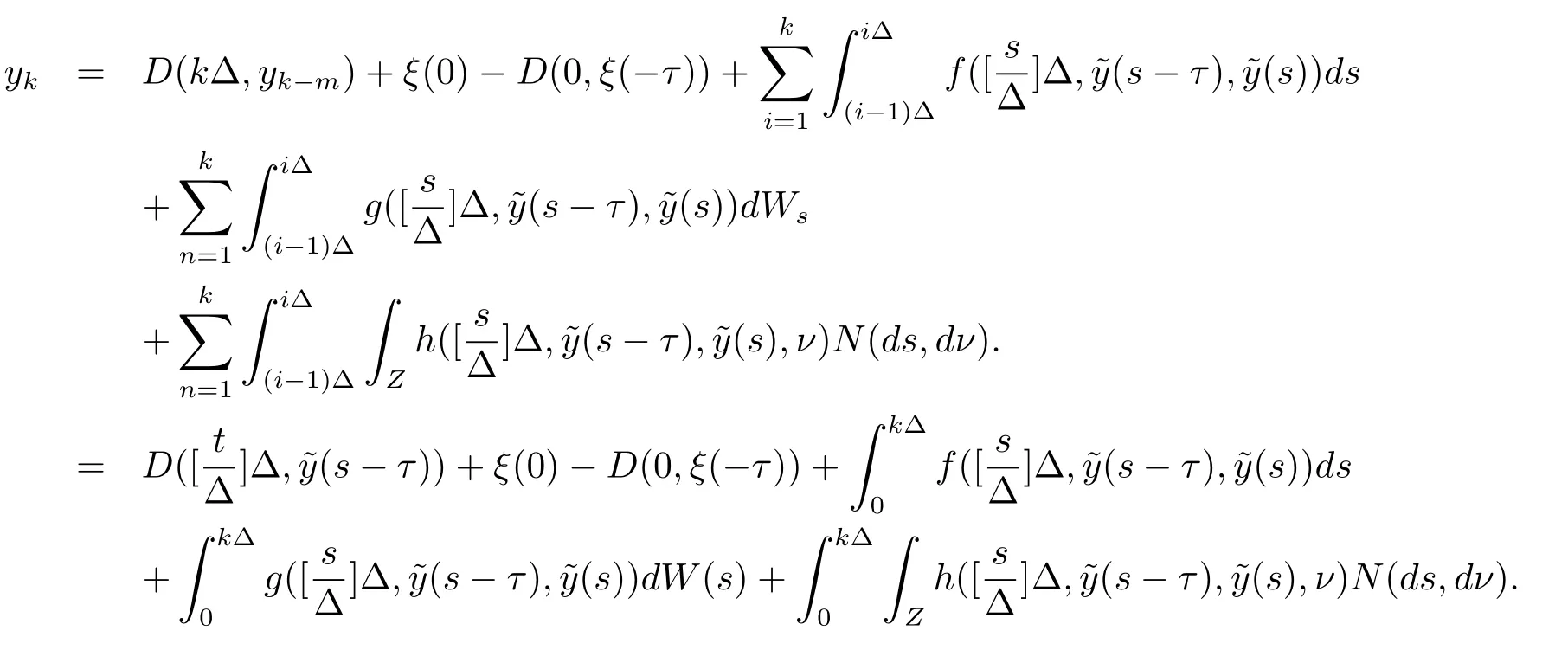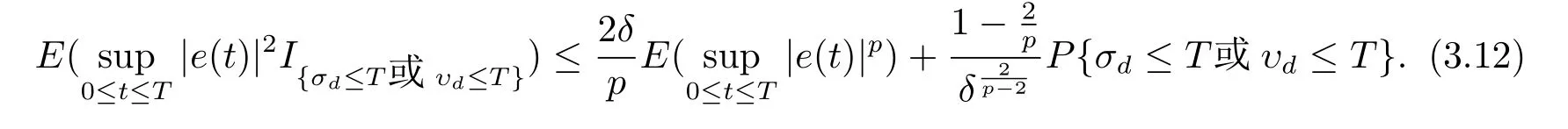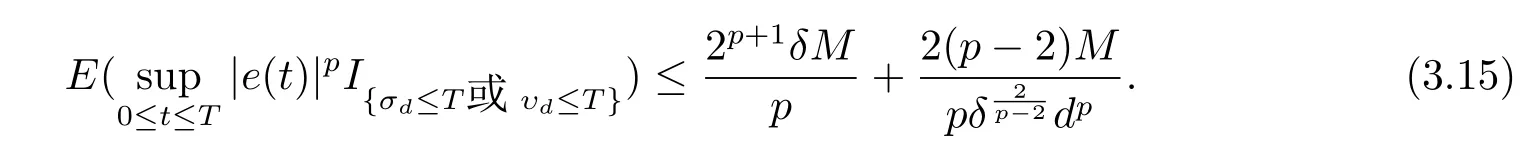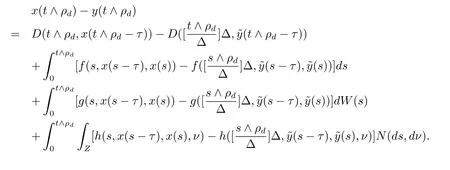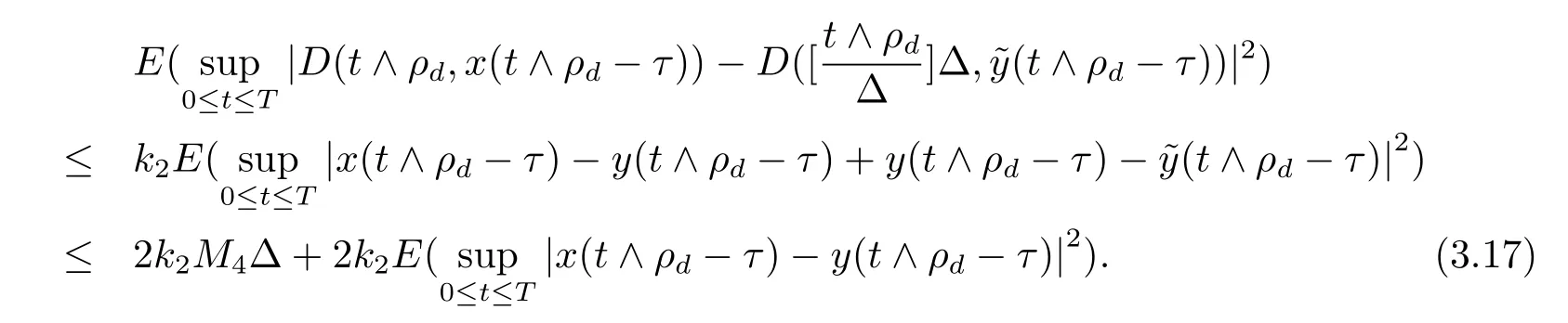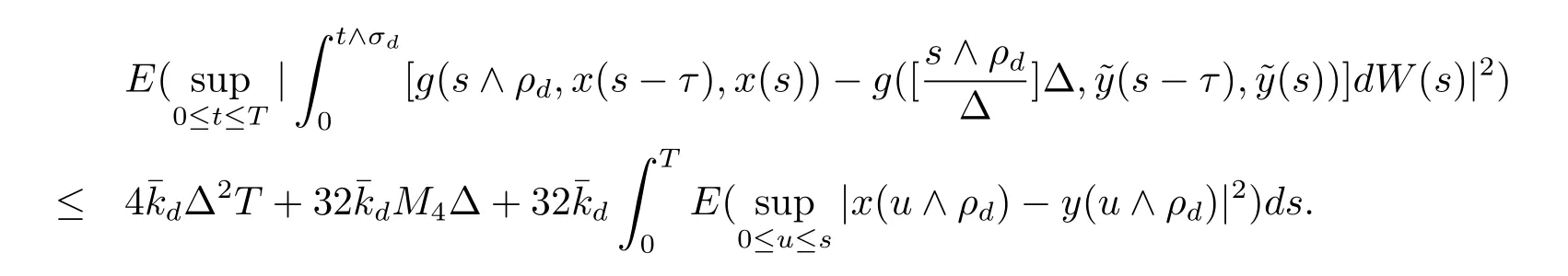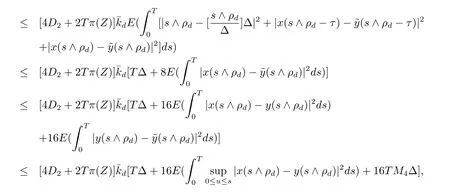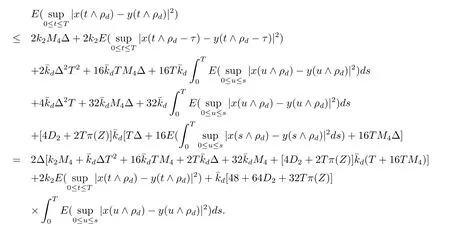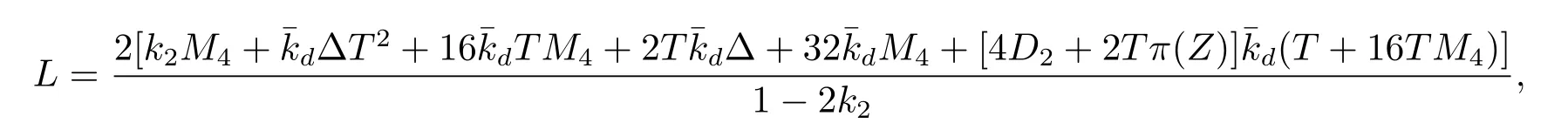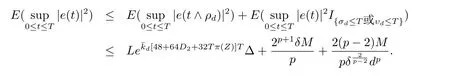帶Lévy 跳的中立隨機微分方程的EM 逼近
馬 麗,嚴良清,韓新方
(海南師范大學數學與統計學院,海南海口571158)
1 引言
中立延遲隨機微分方程歷年來在生物、工程、金融等各個領域引起了學者的廣泛關注.文[1]系統地介紹了不帶跳的隨機泛函微分方程的基本理論及其在金融、隨機游戲、人口問題中的應用;文[2]給出了帶有Lévy 跳隨機泛函微分方程解的存在唯一性;文[3]得到了一類帶Lévy 跳的中立隨機泛函微分方程解的存在唯一性;文[4]研究了帶有特殊跳(泊松跳)的中立隨機延遲微分方程的數值逼近;文[5]得到了Lévy 噪聲擾動的混合隨機微分方程的Euler 近似解;文[6]和文[7]研究了帶Markov 狀態轉換的跳擴散方程的數值解.
設(?,F,P)是完備概率空間,(Ft)t≥0是其上一個滿足通常條件的適應流. 設{=(t),t ≥0}是一個關于(Ft)t≥0適應的穩定的Rn值泊松點過程. 設B(Rn?{0})為Rn?{0}上的波萊爾σ-代數,對A ∈B(Rn?{0}),定義與聯系的泊松計數測度N(t,A)=N((0,t]×A)如下

則存在一個σ 有限測度π 使得
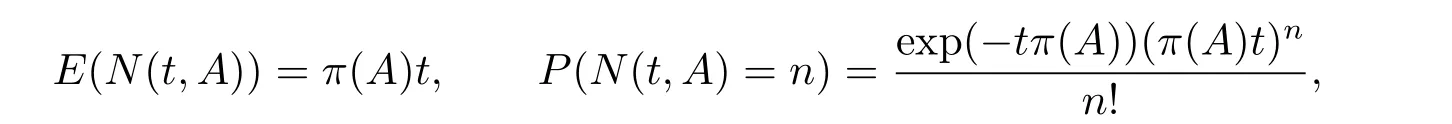
這里的測度π 稱為Lévy 測度.由Doob-Meyer 分解定理,存在關于(Ft)t≥0適應的唯一的鞅和唯一的增過程使得
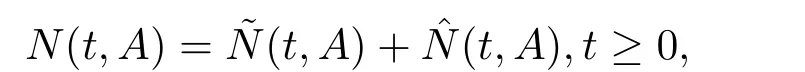
設|·|表示歐式空間Rd中的范數,τ 為一個正的固定的延遲,C([?τ,0],Rd)為[?τ,0]到Rd上的連續函數類,其上的范數為設ξ(t)為關于F0可測的C([?τ,0],Rd)隨機變量且滿足Eξp<∞,其中p 為大于等于2 的任意正整數. 設W(t)是(?,F,P)上關于流(Ft)t≥0適應的標準的r 維布朗運動且與跳N 獨立. 設Z ∈B(Rn?{0})且π(Z)<∞,設0 在系數滿足局部Lipschitz 條件和線性增長條件,中立項D(t,x(t ?τ))關于第二個分量為壓縮映射的條件下,類似于文[2],我們可得方程(1.1)存在唯一解.由于解沒有顯示表達,因此有必要研究其數值解.如果數值解逼近于真實解,我們可以用數值解來估計真實解. 本文內容安排如下:第二節介紹了方程(1.1)的Euler 的數值算法,并給出主要結果即定理1;第三節給出定理1 的證明.本文推廣了文[4]的結果,考慮的中立項是時間和狀態的二元函數,在逼近的時候對中立項需要加一定的條件才可以放縮.此外,有中立項時需要把它看成一個整體,進而用伊藤公式,再由基本不等式及壓縮映射最終得到數值解穩定于真實解.方程(1.1)中f,g,h 也依賴于時間,因此需要三個函數關于時間t 是局部Lipschitz 的. 下面給出(1.1)式的EM 逼近解. 其中?Wk=Wtk+1?Wtk.假設則EM 逼近解y(t)的連續形式如下 本文對系數做如下假設. (H1) 對任意的正整數m,存在正整數使得對任意的t1,t2∈[0,+∞),任意的且|x|≤m,|y|≤m,|有 (H2)對任意的p ≥2,存在正數k1使得對任意t ∈[0,+∞),x,y ∈Rn,有 (H3)存在正數k2∈(0,1),使得對任意t1,t2∈[0,+∞),x,y ∈Rn,有 設T ∈[0,+∞)為任一常數,本文主要結果如下. 定理1在(H1)–(H3)條件下,方程(1.1)的Euler 數值解收斂到真實解.即 在證明定理1 之前,需要一些重要的引理. 引理1在(H1)–(H3)條件下,對任意p ≥2,存在一個獨立于?的常數M>0,使得 證不失一般性,假定x(t)是有界的,否則的話,對每個整數n,定義停時τn=inf{t ∈[0,T]:|x(t)|≥n},考慮停止過程x(t ∨τn)即可.由基本不等式、假設(H3)及不等式可得 因此對任意的t1∈[0,T],有 顯然有 由BDG 不等式及假設(H2)可得 其中Cp為與p 有關的正的常數.對于跳部分,由假設(H2)及文[3]引理3.2,得 其中Dp為正的常數.注意到對任意的t1∈[0,T],有 將(3.2)–(3.4)式代入(3.5)式得 因此 從而定理得證. 下面先建立兩個停時, 引理2在假設(H1)–(H3)下,有 這里C1是獨立于?的正的常數. 證對任意的t1∈[0,T], 證明方法與引理1 的方法相同,這里其證明省略. 推論3在假設(H1)–(H3)下有 這里的M2是一個正的常數且獨立于?. 證對任意的t ∈[0,T ∧ρd],存在k 使得t ∈[tk,tk+1),注意到 因此 又 因此 由基本不等式及假設(H2)可得 由推論3,文[2]引理3.2 及文[9]中Lyapunov 不等式得 取M3=3k1T[1+r+2π(Z)](1+2M2)即可,其中r 為布朗運動的維數. 定理1 的證明假設e(t)=x(t)?y(t),易知 因此對任意的δ>0,有 根據引理1,有 由基本不等式得 將(3.13),(3.14)式代入(3.12)式得 根據x(t)和y(t)的定義,有 類似于引理4 中的證明可知 不妨令M4=3k1[1+2M2](?+m+2π(Z)),則 由假設(H3)及(3.16)式知 由假設(H1)及H?lder 不等式可得 由假設(H1)及BDG 不等式可得 由假設(H1)及文[2]引理3.2 可得 因此 設 將(3.15)、(3.18)式代入(3.11)式得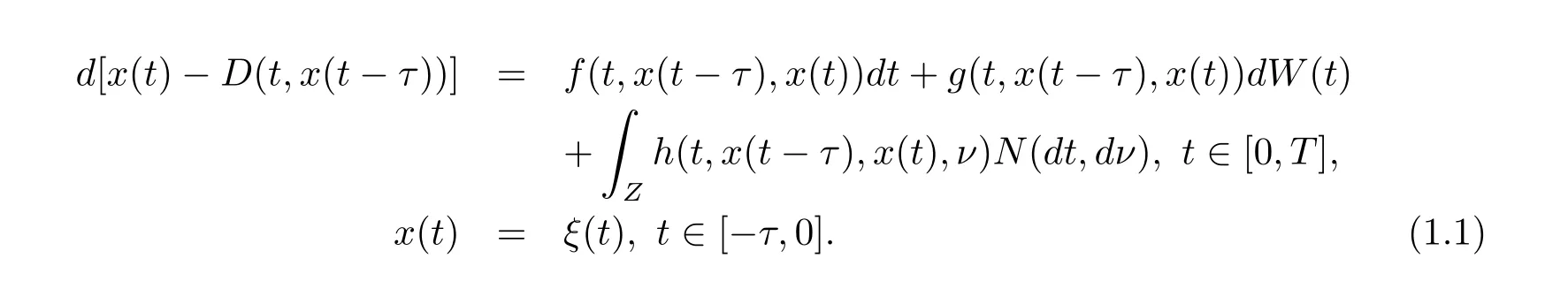
2 EM 近似解及主要結果
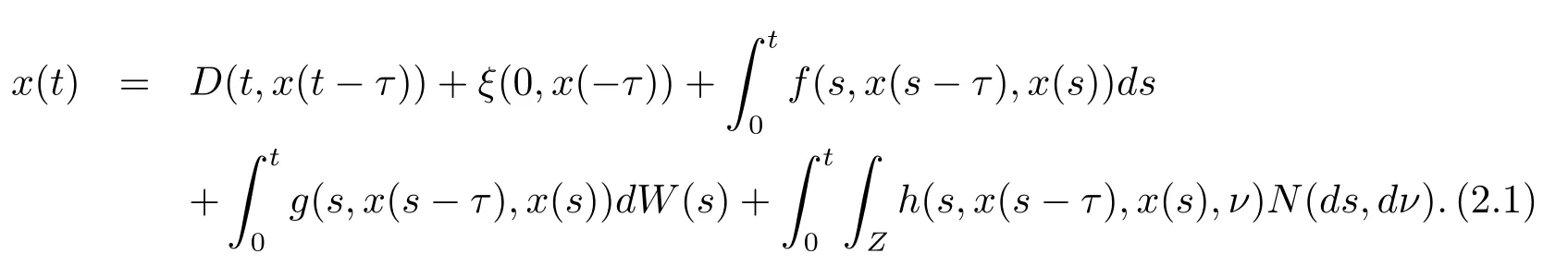
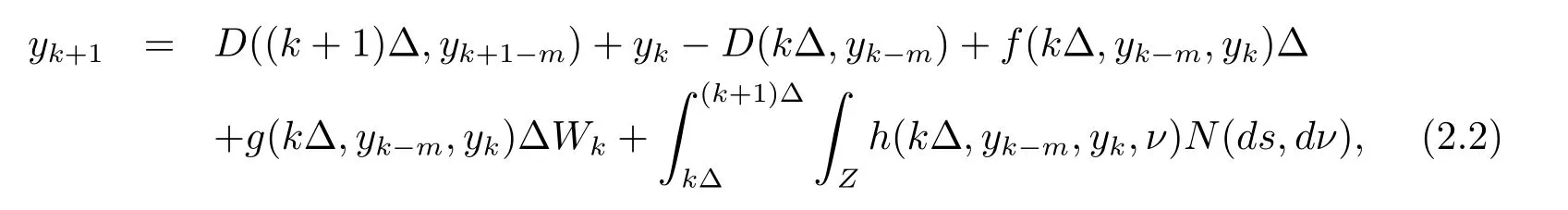
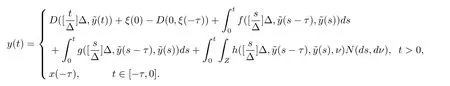
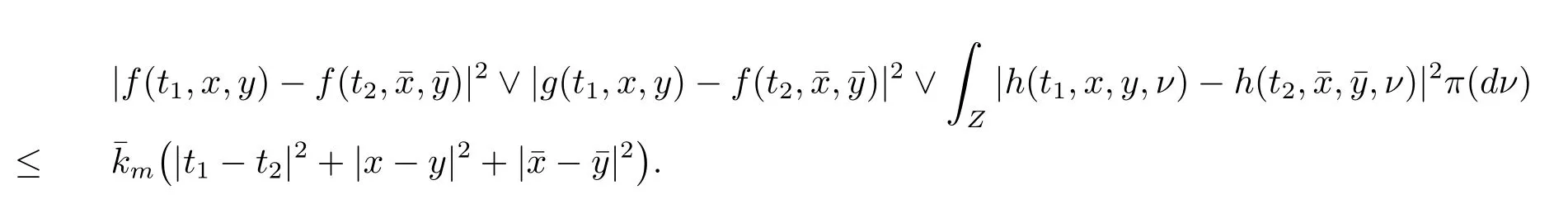
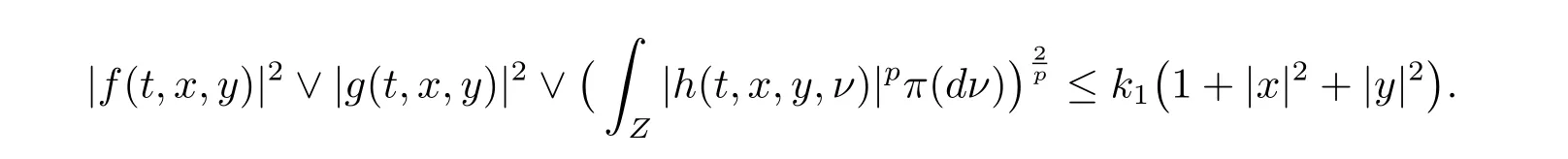
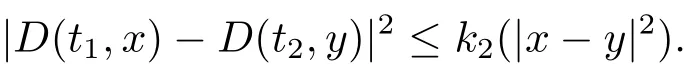
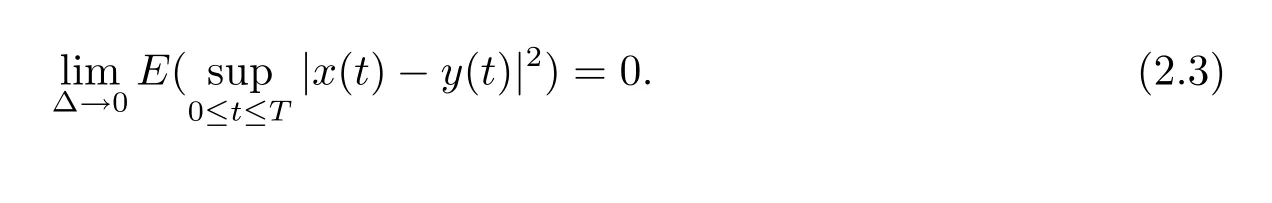
3 定理1 的證明