單參數Chen 系統的部分狀態線性化同步

李德奎

(甘肅中醫藥大學理科教學部,甘肅定西743000)

1 引言

1990 年,Pecora 和Carroll 首次提出了混沌同步概念并實現了混沌系統的同步[1],為混沌同步的理論研究及應用奠定了基礎.近年來,混沌同步得到許多學者的廣泛研究,并提出了許多混沌同步方法[2?5].理論上能夠實現混沌系統的各種同步,如完全同步、投影同步、相同步等.大多數混沌系統同步就要對其全部狀態變量施加較復雜的線性或非線性控制器[6?8],實際應用中混沌同步是較難實現的,主要原因是混沌系統的內隨機性和外部不確定因素的干擾,同時系統內部的不確定性和系統的狀態變量較多,對其全部狀態變量實施控制是不現實的.

為此,設置最簡單的控制器,控制盡可能少的系統狀態變量,實現混沌系統的全部狀態變量同步是混沌同步研究的不懈的追求．劉洪娟等人研究了參數未知的統一混沌系統中的混合同步現象[9],僅通過對一個變量實施線性反饋控制,實現了統一混沌系統同步．然而線性反饋控制要測試反饋增益系數的大小,反饋系數過大或過小都會影響系統的同步.文獻[10]基于反饋線性化方法對R?sler 混沌系統的一個變量實施控制,將混沌系統轉化為一個線性系統.

文獻[11]提出的單參數Chen 系統,該系統結構形式簡單,且只含有一個系統參數,同時當唯一的參數a=8 時,系統正的Lyapunov 指數為2.475.因此該系統具有較強的混沌特性,同時電路實現容易,在保密通信領域具有潛在的應用價值.

基于以上討論,本文根據非線性系統相對階的概念和Lie 導數運算方法,應用反饋線性化策略,對單參數Chen 系統進行部分狀態線性化,同時設計控制器僅對響應系統的一個變量實施控制,實現單參數Chen 系統的同步.

2 非線性系統反饋線性化的條件

考慮一個受控的n 維輸入輸出系統

式中x=[x1(t),x2(t),···,xn(t)]T∈Rn為系統的狀態變量;f:Rn→Rn和g:Rn→Rn為光滑向量場,u ∈R1為系統的控制輸入;h:Rn→Rn為光滑的輸出函數.

系統(2.1)的反饋線性化問題是尋找坐標變換z=φ(x)和控制器u=α(x)+β(x)v,將系統(2.1)變為線性系統其中v 為變換后的系統控制輸入.為了給出系統(2.1)的線性化條件.下面首先介紹相對階的概念.

定義1設x0∈X,如果存在x0的鄰域V 和r ∈Z+,使得系統(2.1)滿足下列條件

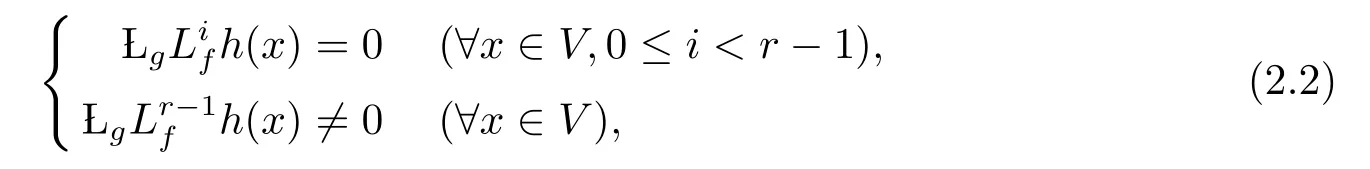
那么稱系統(2.1)在點x0具有相對階r,其中Lfh(x)=?hf 為函數h(x)對f(x)的Lie 導數,Lie 導數Lfh(x)是h(x)沿著向量f 方向的方向導數且有

對系統(2.1)的輸出y 求導,并根據(2.2)式,得出相對階r 與輸入量u 的關系為

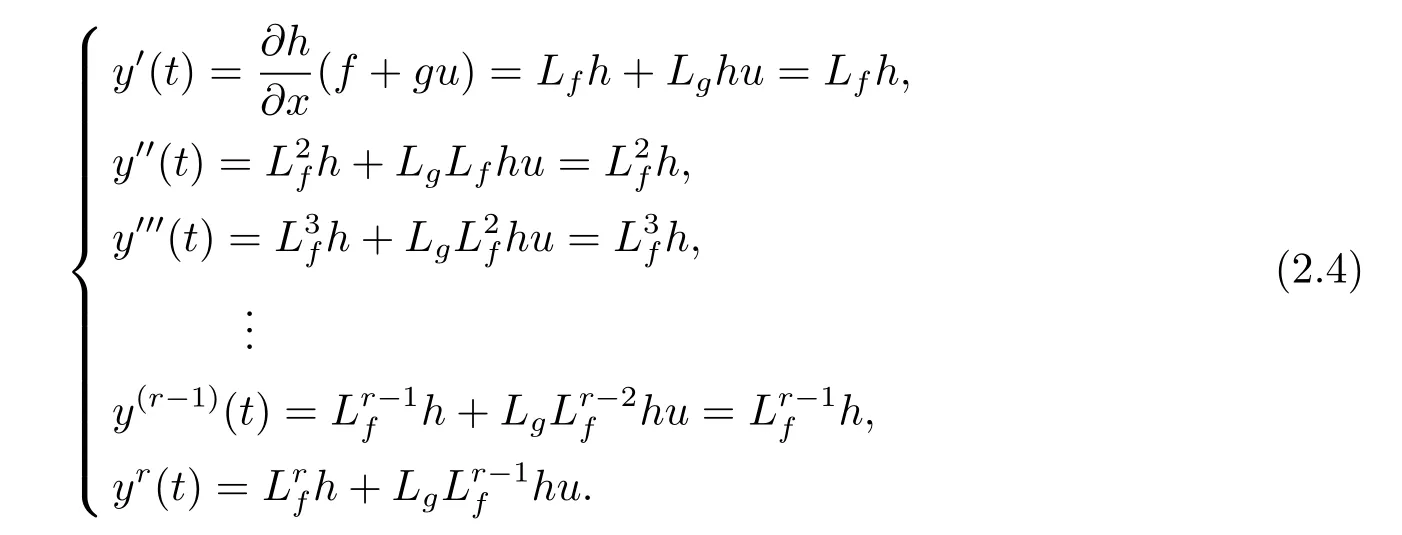
由(2.4)式表明,如果系統(2.1)具有相對階r,則系統輸出的小于r 階的導數與輸入u 無關,只有系統輸出的r 階導數與輸入u 有關.若系統(2.1)沒有相對階,則即系統的輸出與輸入u 無關.

不是所有的系統都可進行線性化,可線性化的系統需要滿足一定的條件,下面給出系統(2.1)可線性化的一個充分必要條件.

定理1n 維非線性系統可線性化的充分必要條件是存在一個光滑函數h(x),使得系統

在x0點具有相對階n.

定理1 給出了系統(2.1)可線性化的充分必要條件,定理1 的證明較復雜,這里不再敘述,證明過程見文獻[11].如果定理1 的條件被滿足,則存在坐標變換

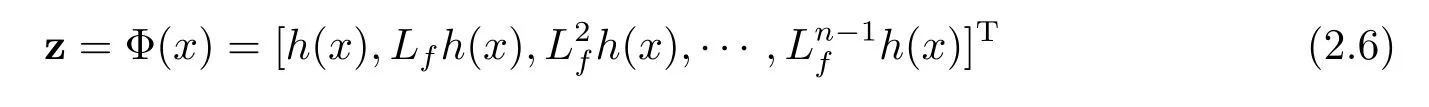
和系統的控制輸入

其中v 是新的輸入

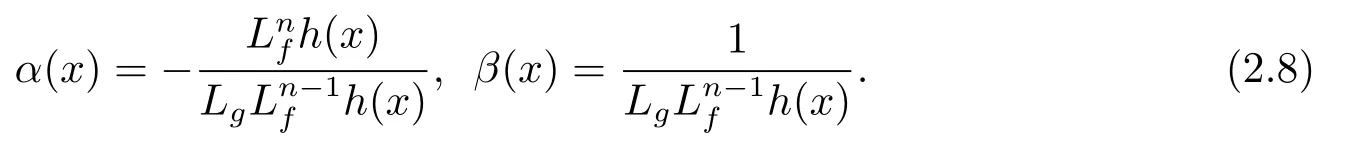
將系統(2.1)變為線性系統

3 單參數Chen 系統的反饋線性化

單參數Chen 系統[12]的動力學方程為

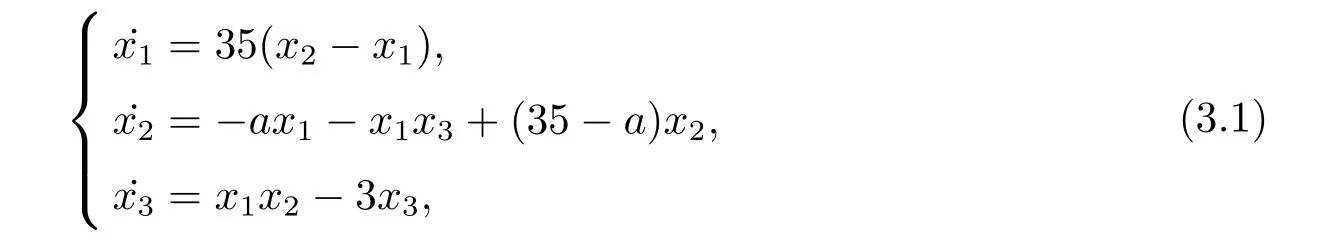
其中x1,x2,x3為狀態變量,a 是系統參數.當a=32 時,系統(3.1)就演變成了Chen 混沌系統;當參數a=8 時,由Kaplan-Yorke 猜想公式,計算出系統(3.1)的維數D=2.18,說明系統(3.1)具有分數維.此時系統(3.1)的Lyapunov 指數為λ1=?13.23,λ2=?10,λ3=2.22.說明當參數a=8 時,系統(3.1)處于混沌狀態,具有如圖1 所示的奇怪吸引子.

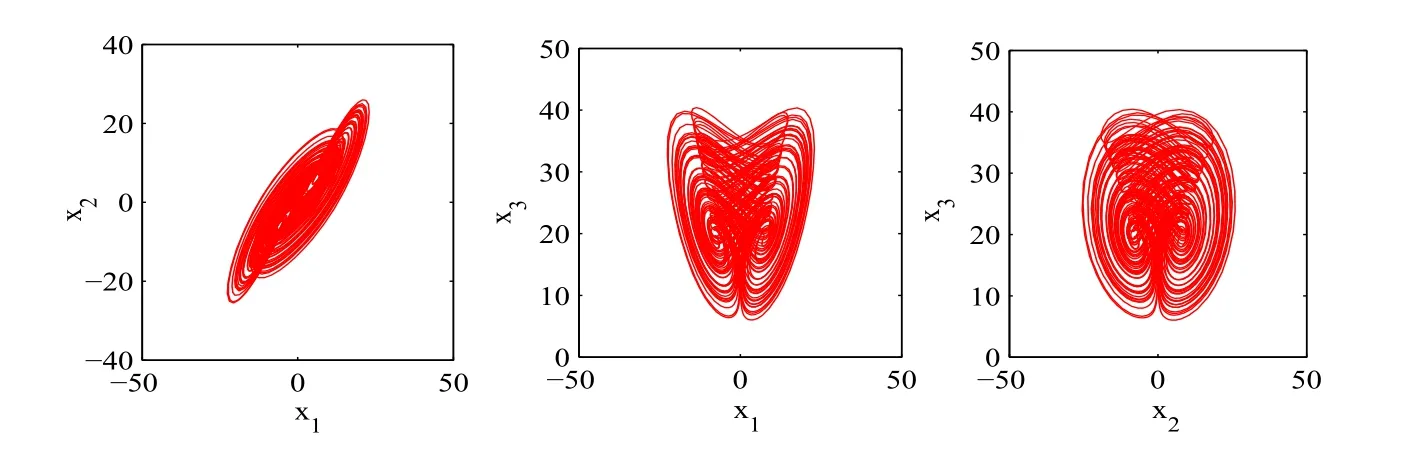
圖1:單參數Chen 混沌系統的奇怪吸引子

將系統(3.1)看作是驅動系統,受控的響應系統描述為

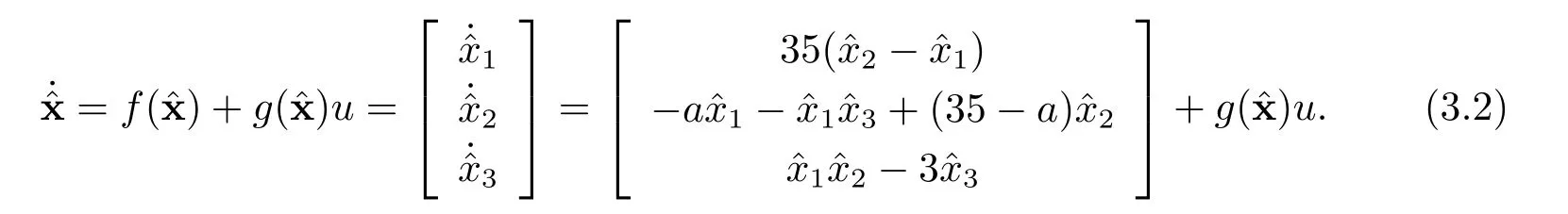
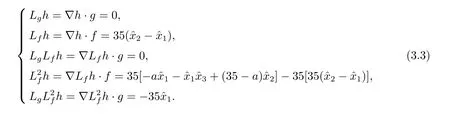
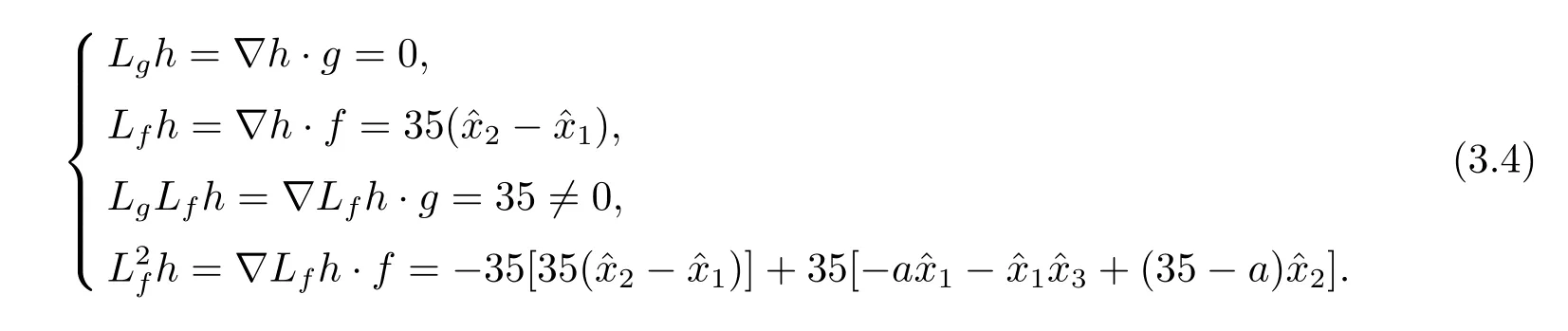
根據系統相對階的定義和響應系統(3.2)的各階Lie 導數(3.4)可以看出,響應系統(3.2)的相對階為r=2.根據(2.6)式,得到響應系統(3.2)的坐標變換為

將響應系統(3.2)部分狀態線性化為

下面相應地對驅動系統(3.1)進行線性化,取z1=x1=λ(x),則有

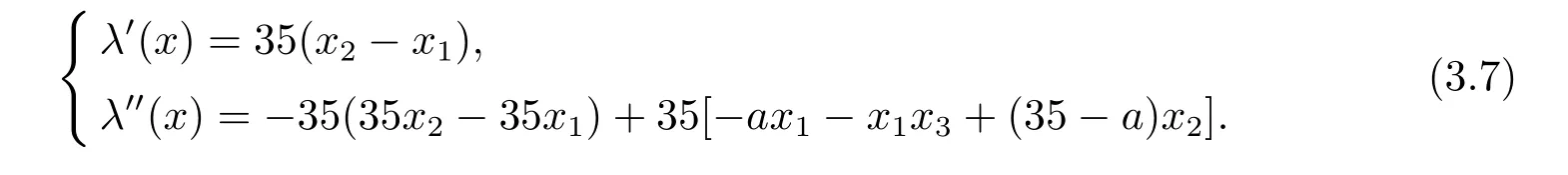
驅動系統(3.1)通過坐標變換

可轉化為下列形式

4 單參數Chen 系統的同步

設驅動系統(3.1)和響應系統(3.2)的同步誤差為

設驅動系統的線性化系統(3.9)和響應系統的線性化系統(3.6)的誤差為

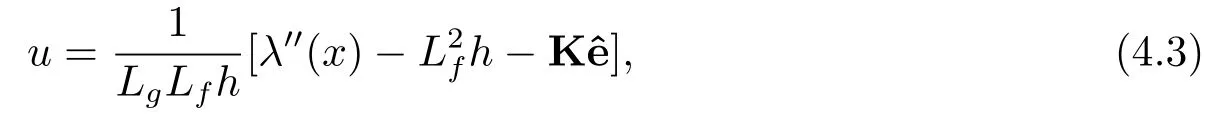
其中K=(k1,k2)的選取使得多項式P3(s)=s2+k2s+k1是Hurwitz 穩定的.

定理2在控制器(4.3)的控制作用下,驅動系統(3.1)和受控的響應系統(3.2)能夠實現同步.

證根據(4.2)式,坐標變換后的誤差系統為

將(3.6)式和(3.9)式代入(4.4)式可得

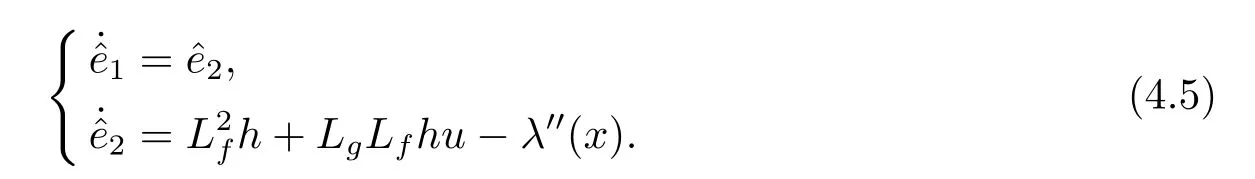
將(4.3)式和(4.5)式得

將(3.5)式和(3.8)式代入同步誤差(4.1)式和(4.2)式可得

當e1→0、e2→0 時,有從而e3=e?3t→0.綜上可得,當t →∞時,ei→0(i=1,2,3),從而在控制器(4.3)作用下,驅動系統(3.1)和響應系統(3.2)實現全部狀態完全同步.

5 數值仿真

取參數a=8,此時系統(3.1)處于混沌運動狀態,取K=[4,4],初值條件分別為和同步控制器(4.3)重寫為

采用四階龍格–庫塔方法,用控制器(5.1)控制響應系統(3.2)的第二個狀態變量,所得驅動系統(3.1)和響應系統(3.2)的同步誤差曲線如圖2 所示.

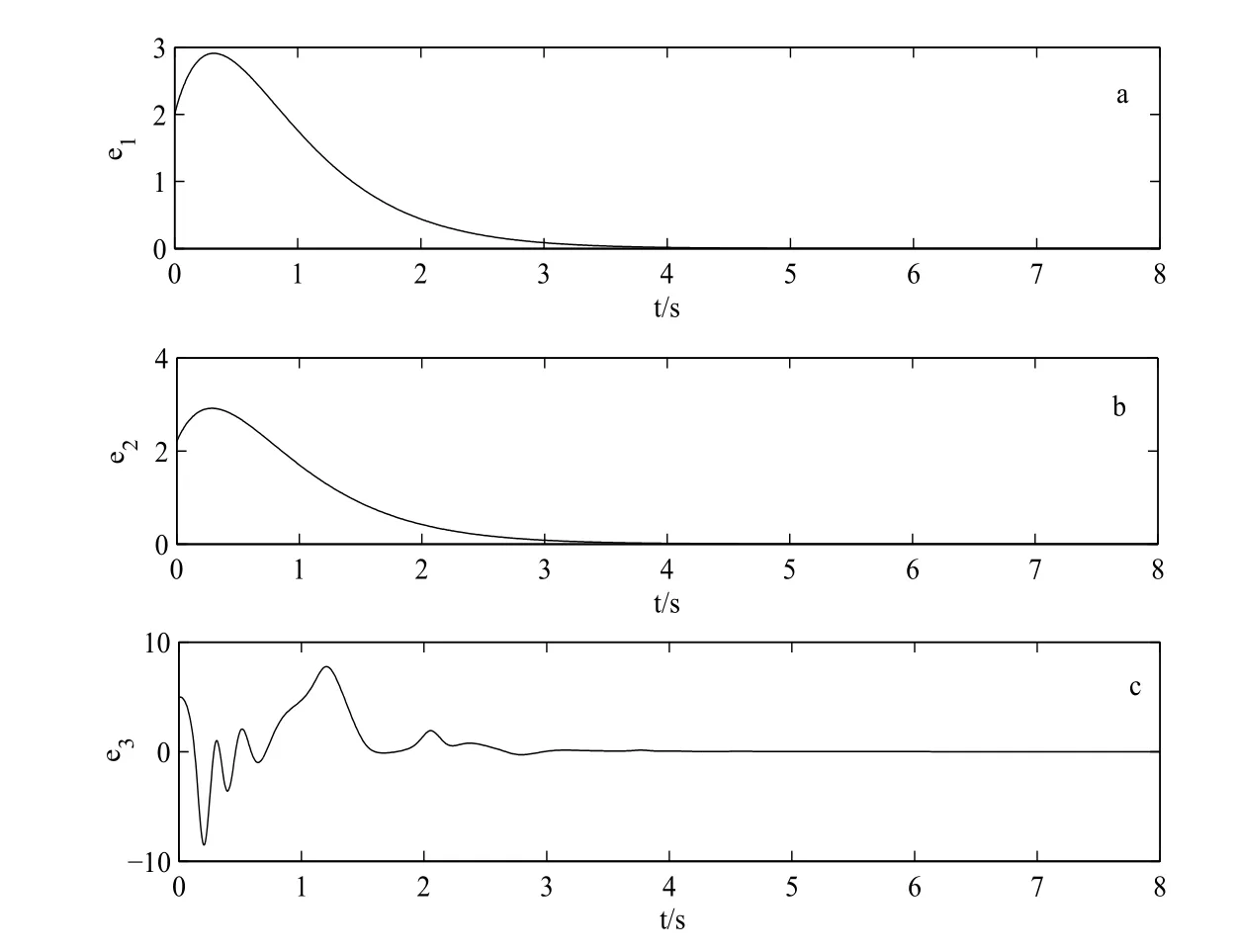
圖2:驅動系統(3.1)和受控響應系統(3.2)同步誤差曲線圖

由圖2 可知,驅動系統(3.1)和受控響應系統(3.2)的同步誤差ei(i=1,2,3)都快速趨向0,說明利用控制器(5.1)僅對響應系統的第二個狀態變量實施控制,驅動系統(3.1)和受控響應系統(3.2)就能快速實現全部狀態同步.

在不同初值條件[x1(0),x2(0),x3(0)]=[10,?0.2,0.1]和=[12,2,5]下,在同一坐標系中做出驅動系統(3.1)的狀態變量(x1,x3)和受控響應系統(3.2)的狀態變量的相圖(如圖3 所示),其中實線圖表示驅動系統的相圖,虛線圖表示響應系統的相圖.

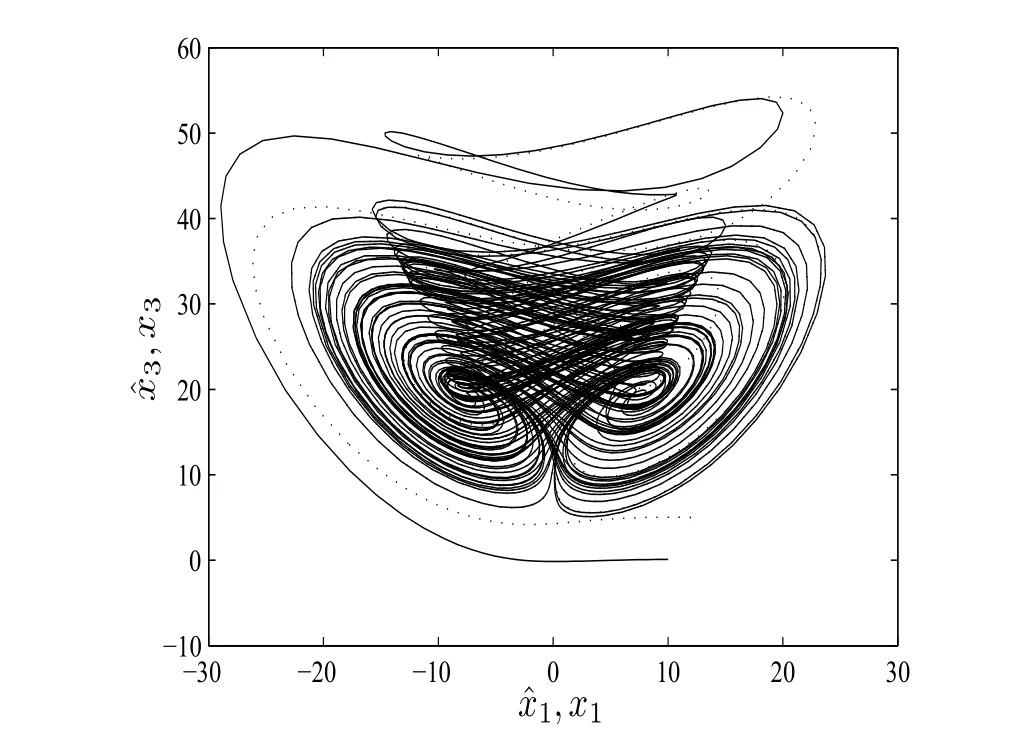
圖3:驅動系統（3.1）和受控的響應系統（3.2）的相圖

由圖3 可知,驅動系統(3.1)和受控的響應系統(3.2)在不同的初值條件下,它們的相圖軌線很快趨于重合,說明它們實現了同步.

6 結論

根據任意非線性輸入輸出系統相對階的定義,給出了n 維非線性系統反饋線性化的充分必要條件是相對階r=n.也就是說系統的相對階2 ≤r

基于狀態線性化系統,實現混沌系統同步是混沌同步的研究方法之一.同時,控制盡可能少的狀態變量,實現混沌系統的全部狀態同步是混沌同步控制的不懈追求.一般情況下,要實現混沌系統的全部狀態同步,就要對其全部狀態變量實施控制.然而對單參數Chen 系統進行部分狀態線性化的過程中,通過對誤差系統的分析發現,僅對響應系統的第二個狀態變量實施控制,就能實現單參數Chen 系統的全部狀態同步,數值仿真也表明理論分析的正確性和同步控制器的有效性,這也是本文的創新所在.當然對于一個可線性化的多參數混沌系統,是否僅對其一個狀態控制就能實現其全部狀態同步呢?這要通過對誤差系統的具體分析來確定.