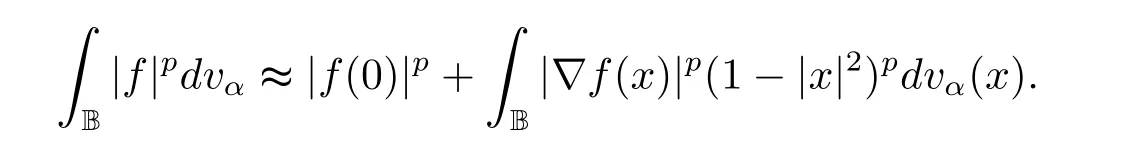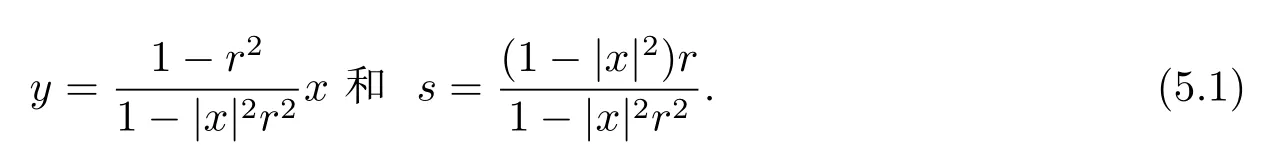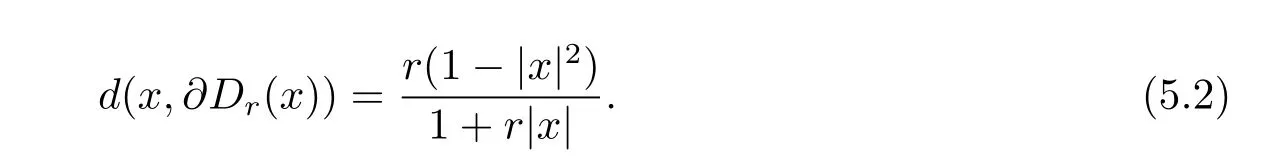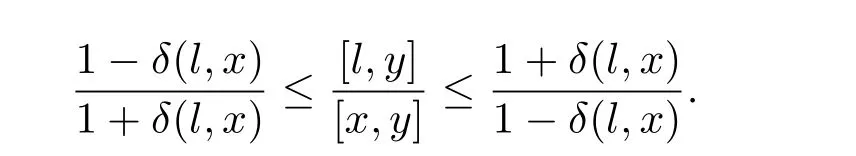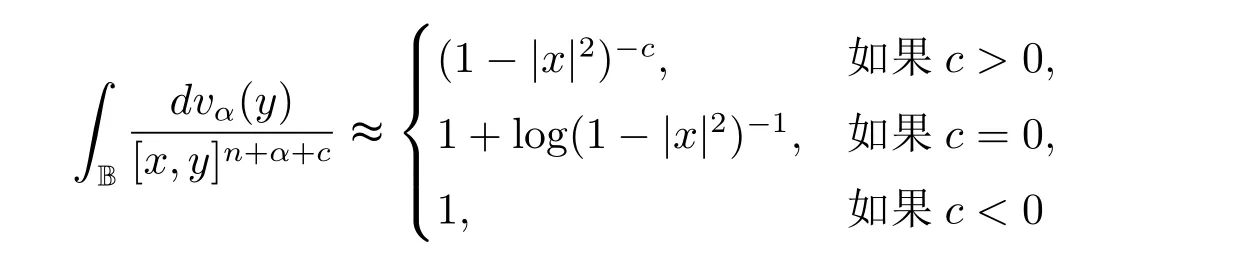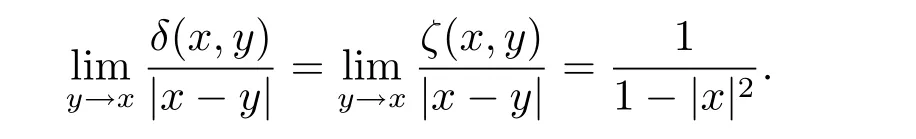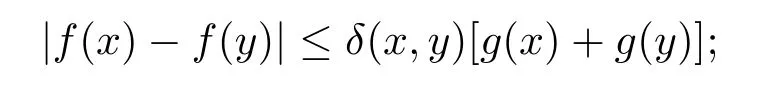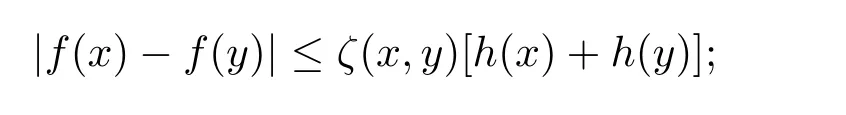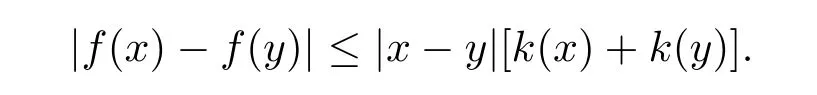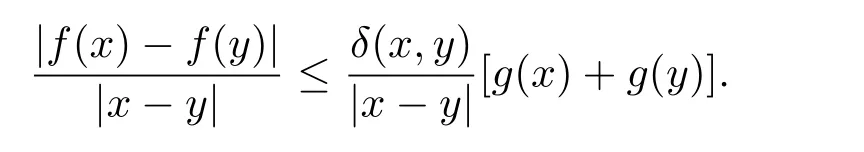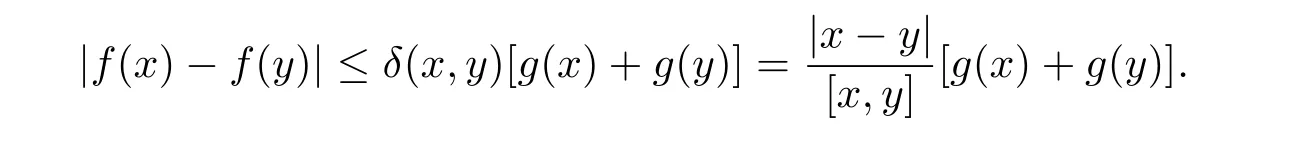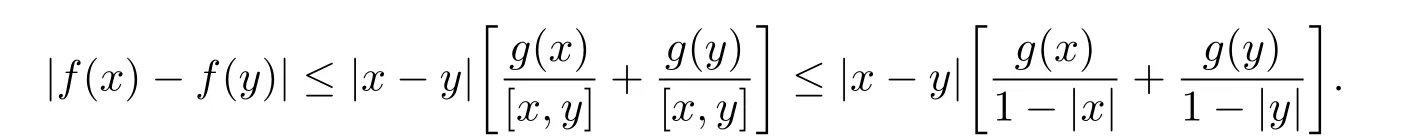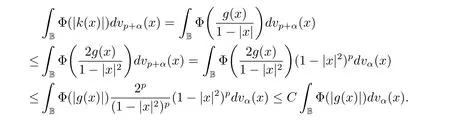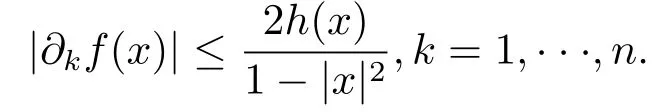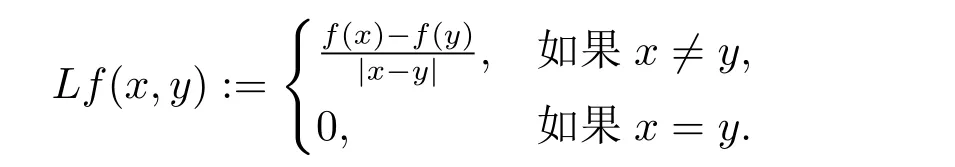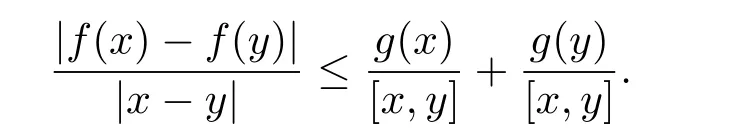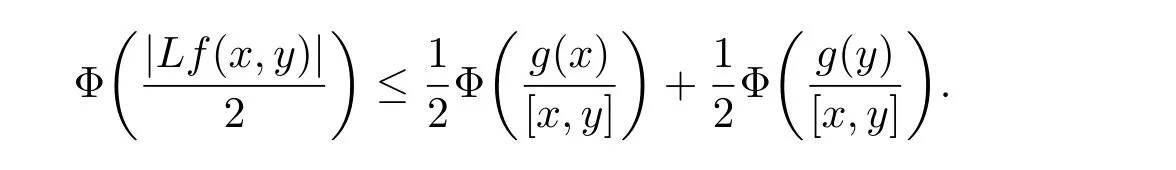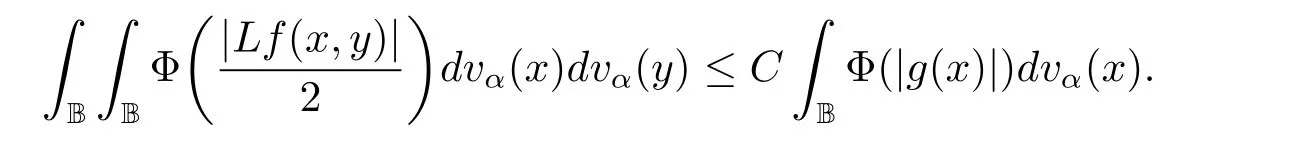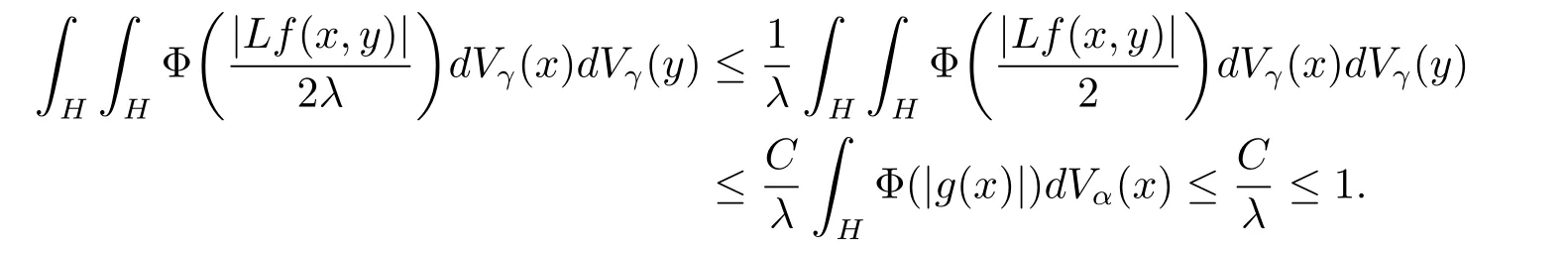調和Bergman-Orlicz 空間的Lipschitz 型刻畫
馬茹夢,徐景實
(海南師范大學數學與統計學院,海南海口571158)
1 引言
對于區域? ?Rn,用h(?)表示? 上的復值調和函數構成的空間.對于一個固定的正整數n ≥2,用H=Rn?1×R+表示上半空間,其中R+表示所有正實數構成的集合.設α 為實數,用表示H 上的加權測度.給定一個凸函數Φ:[0,∞)→[0,+∞),稱Φ是一個增長函數如果它是連續的且非減的函數.對于增長函數Φ,Orlicz 空間
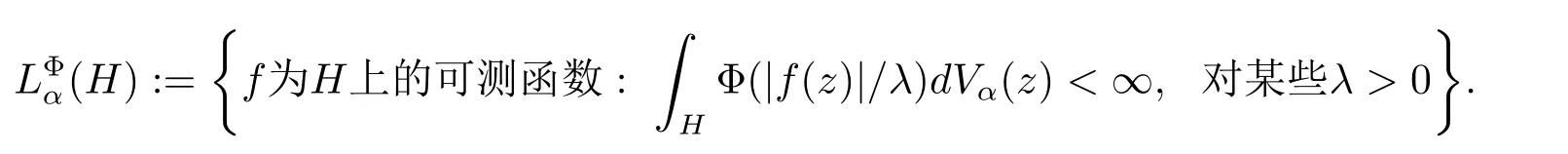
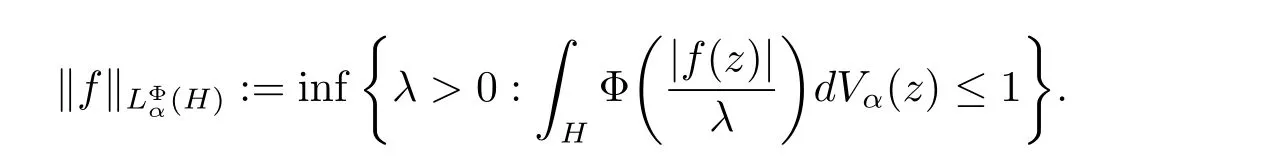
當Φ(t)=tp,t ∈[0,∞)時,Orlicz 空間是Lebesgue空間且對應的調和Bergman-Orlicz空間表示為
烏蘭哈斯和朱克和在文獻[1]中利用歐氏度量、雙曲型度量、偽雙曲型度量給出加權Bergman 空間在復歐氏空間Cn的單位球上的Lipschitz 型刻畫;Kyesook 在文獻[2]中研究了在上半空間H 上的調和Bergman 空間的刻畫.即設α>?1,p ∈(0,∞)和則存在一個正的連續函數使得對所有的z,w ∈H 有
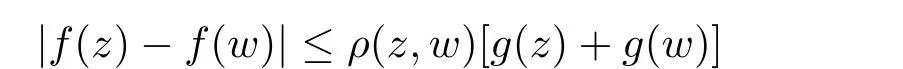
和
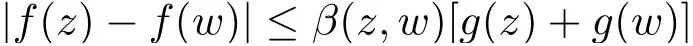
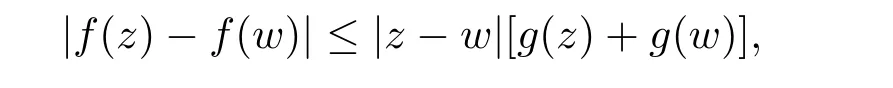
其中ρ 和β 的定義見第二節.文獻[2]還給出了上半空間上調和函數差商的刻畫和歐氏空間中單位球上調和Bergman 空間的刻畫.
受文獻[1,2]的影響,我們將把文獻[2]中的結果推廣到上半空間或單位球上的調和Bergman-Orlicz 空間中.本文后面如下安排:第二節為一些概念和需要的引理;第三節考慮上半空間上的調和Bergman-Orlicz 空間;第四節給出上半空間上的調和函數差商的有界性;第五節得到單位球上的調和Bergman-Orlicz 空間的Lipschitz 型刻畫.在本文中符號表示存在一個正常數C 使得A ≤CB.如果且則記為A ≈B.
2 預備知識
在這一節,介紹一些概念和后面將會用到的引理.
定義H 上的雙曲型度量β 為
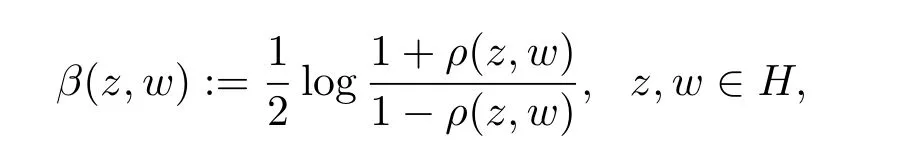
其中
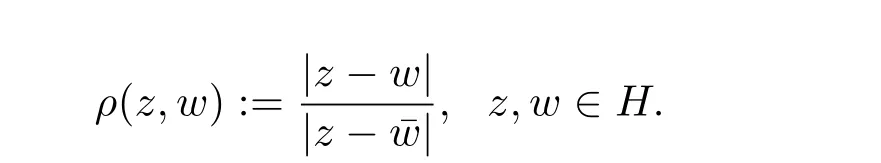
H 上的偽雙曲型度量ρ 是平移不變和伸縮不變的,且ρ 是H 上的距離函數,見文獻[3]中的引理3.1.
符號Ba(x)表示以a>0 為半徑x ∈Rn為中心的歐氏球.對于z ∈H 和r ∈(0,1),設Er(z)表示以r 為半徑z 為中心的偽雙曲型球.易得Er(z)為歐氏球Ba(x),其中
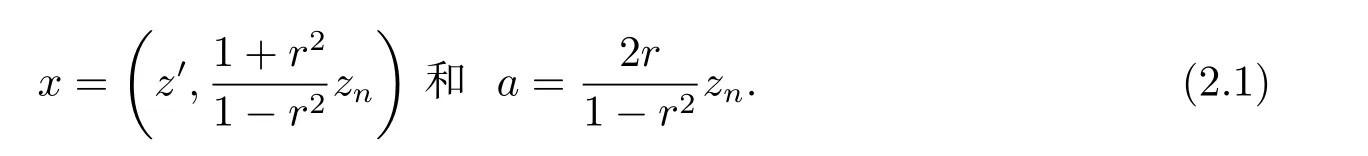
設d(x,?)是點x 到集合? ?Rn上的歐氏距離.則有

引理2.1[3]若z,w ∈H,則
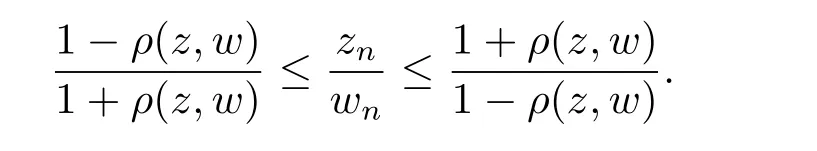
引理2.2[3]若z,w ∈H,則
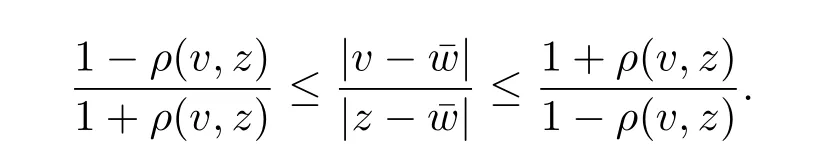
給定r ∈(0,1),由以上的引理可得

設dw 是Rn上的Lebesgue 測度.以下引理可參考文獻[4]中的引理3.5 或者文獻[5]中的定理HLFS.
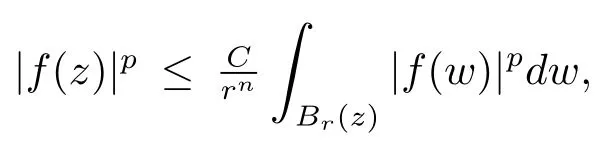
給出多重指標m=(m1,···,mn),其中mi(i=1,···,n)為非負整數,則有|m|=m1+···+mn和其中?i表示對第i 個指標進行求微分.由引理2.3 和Cauchy 估計得下列引理.其證明可參見文獻[6]的推論8.2.
引理2.4[6]設? 為Rn中的一個區域.給定1 ≤p<∞和一個多重指標m=(m1,···,mn).則存在一個常數C=C(p,m)>0,使得對? 上的任意解析函數f 都有
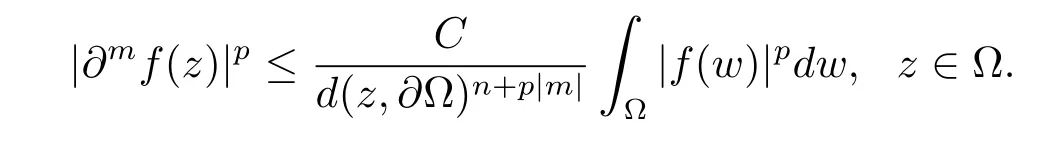
3 上半空間上的調和Bergman-Orlicz 空間
本節的主要定理如下.
定理3.1設α>?1,Φ 是一個增長函數,若則存在一個正的連續函數使得對所有的z,w ∈H,有|f(z)?f(w)|≤ρ(z,w)[g(z)+g(w)].
定理3.2設α>?1,Φ 為增長函數,若則存在一個正的連續函數使得對所有z,w ∈H,有|f(z)?f(w)|≤β(z,w)[g(z)+g(w)].
設p>0,Mp表示存在某個常數C>0 使得對所有的s>0 和t>0,Φ(st)≤CtpΦ(s)成立的凸增長函數Φ 構成的集合.
定理3.3設α>?1,Φ ∈Mp(p>0),若則存在一個正的連續函數使得對所有的z,w ∈H,有|f(z)?f(w)|≤|z ?w|[g(z)+g(w)].
引理3.1[7]給定α>?1,則有

對所有z ∈H 成立.
定理3.1 的證明設固定考慮H 中ρ(z,w) 由引理2.2 知 即 令v=w,則 因此存在兩個正的常數C1,C2使得同理可得由于對任意的w ∈Er(z),zn≈wn,則當w ∈Er(z)時,有.因此|f(z)?f(w)|≤ρ(z,w)h(z),這里 如果ρ(z,w)>r,則由三角不等式得 偽雙曲型距離ρ 滿足三角不等式,因此可以選取r'∈(0,1)使得對任意的a ∈Er(z)都有Er(a)?Er'(z). 由引理2.4,(2.2),(2.3)式和引理2.2 得 由引理3.1 知 則 運用Φ 的凸性和Jensen 不等式得 在H 上對以上不等式關于dVα(z)求積分且運用Fubini 定理可得 定理3.2 的證明由于ρ ≤β,則定理3.1 中的函數g 也使得該定理成立. 定理3.3 的證明設α>?1,Φ ∈Mp(p>0),若則由定理3.1 的證明知存在一個正的連續函數h 使得對所有的z,w ∈H 有 命題3.1給定α>?1,Φ 為增長函數,則存在一個正常數C 使得對所有f ∈h(H),有 證固定α>?1.假設f ∈h(H)和z ∈H.對于每一個固定的0 則 運用Φ 的凸性和Jensen 不等式得 在H 上對以上不等式關于dVα(z)求積分且運用Fubini定理得 本節考慮H 上關于調和函數的差商.給定f ∈h(H),對所有的z,w ∈H 定義 應用定理3.1 可得以下結果. 定理4.1假設α>?1,Φ ∈Mp,p ∈(α+n,∞)且2γ=p+α ?n,則L 有界地映到LΦ(Vγ×Vγ). 證設由定理3.1 知存在一個正的連續函數使得對有 則 故 運用Φ 的凸性,得 因此 在這節考慮Rn上單位球B 上的調和函數.設α 為實數,用vα表示B 上的加權測度,即dvα(x)=(1 ?|x|2)αdx.用dvα替代dVα,類似于空間與空間可以定義空間與空間 下列引理由Hardy 等在文獻[8]中給出n=2 的證明,n ≥3 的情況見文獻[9]. 命題5.1[8,9]給定α>?1 和0 因此有 引理5.1[10]若l,x,y ∈B,則 引理5.2[10]給定α>?1 和實數c,對所有的x ∈B,有 成立. 引理5.3[2]設1 ≤k ≤n,x,y ∈B,y=(x1,···,xk?1,txk,xk+1,···,xn)其中t 是一個標量.則 定理5.1設α>?1,Φ ∈Mp(p>0),f ∈h(B).則下列結果等價. 證(a)(b)類似于定理3.1 的證明可得. 由于[x,y]≥1 ?|x||y|≥1 ?|x|,1 ?|y|.因此 因此得 考慮關于調和函數的差商L 在單位球上的情況.給定f ∈h(B),L 定義為 對于x,y ∈B,由定理5.1 可以模仿定理4.1 的證明,得到在單位球上的類似結果. 定理5.2設α>?1,Φ ∈Mp,n+α 注意到在引理5.2 中c<0 的情況與引理3.1 不同,這個不同可以把上面的調和函數的結果擴展到實單位球上0 定理5.3設α>?1,Φ ∈Mp,0 因此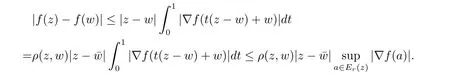
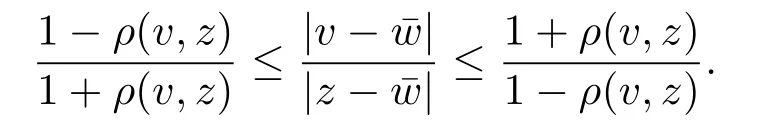
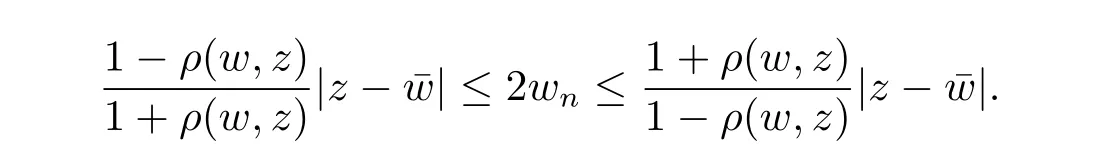
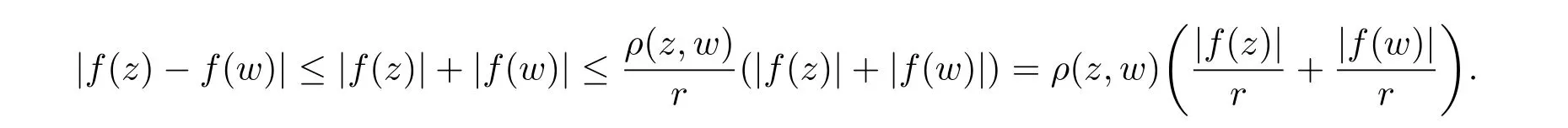
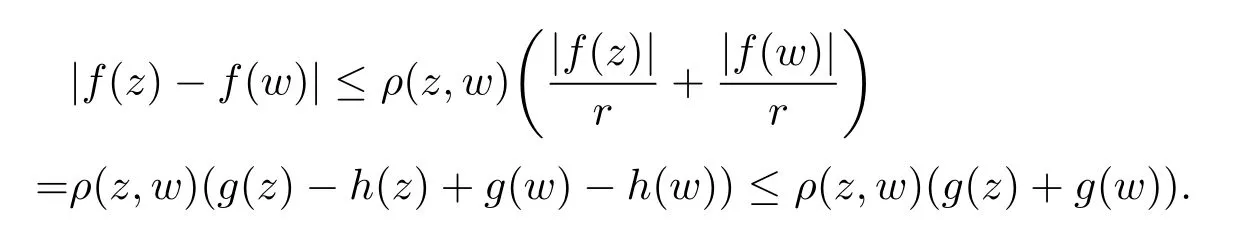
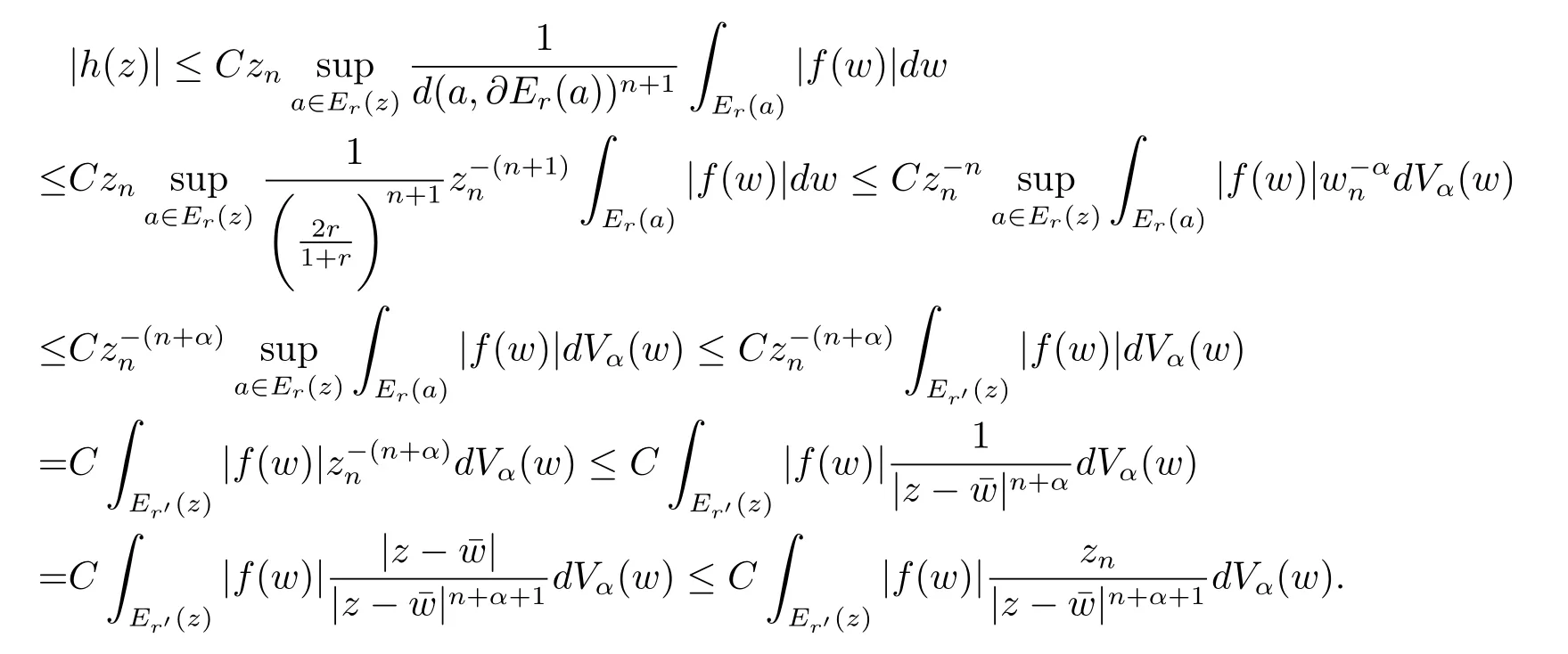
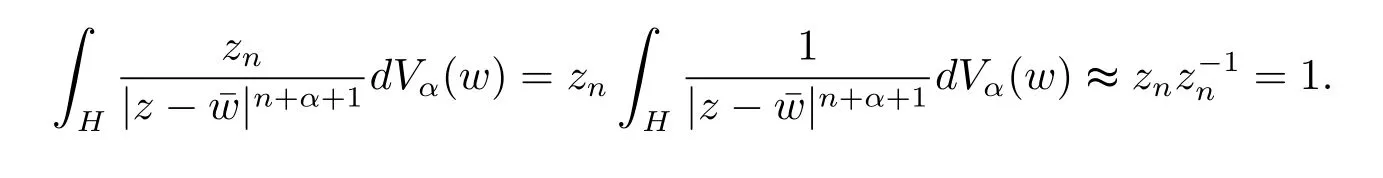
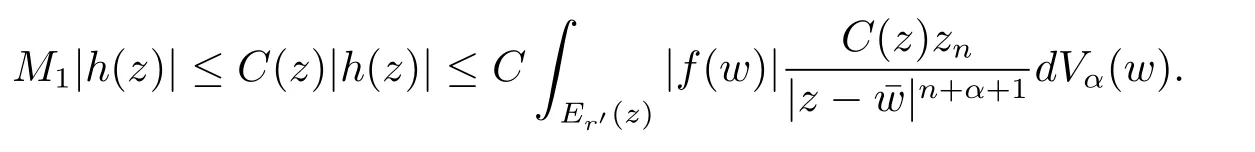
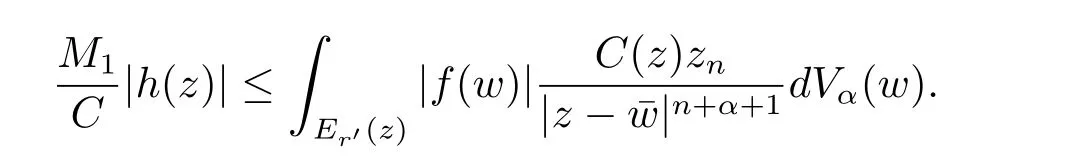
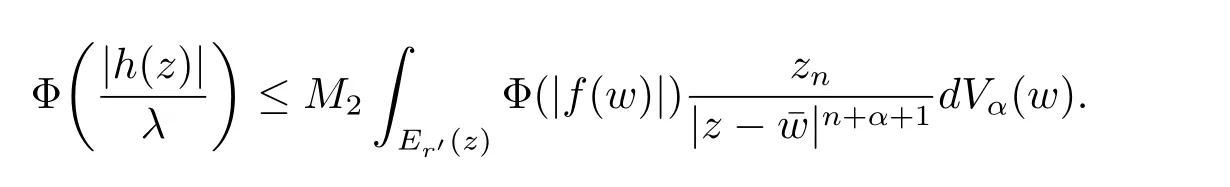
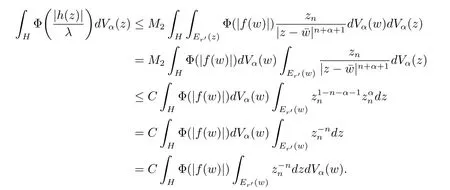
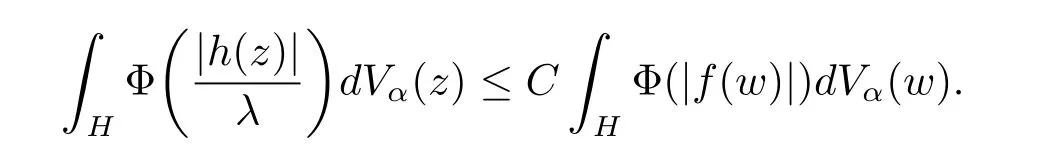
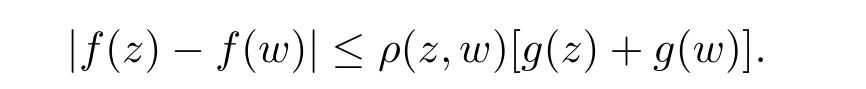

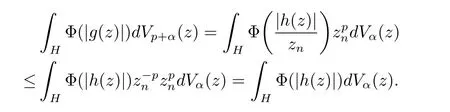
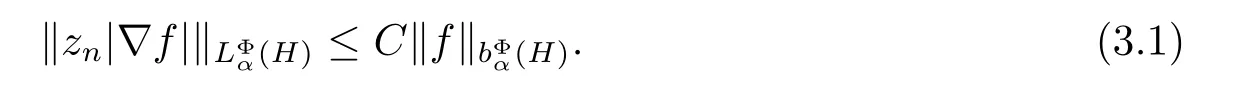

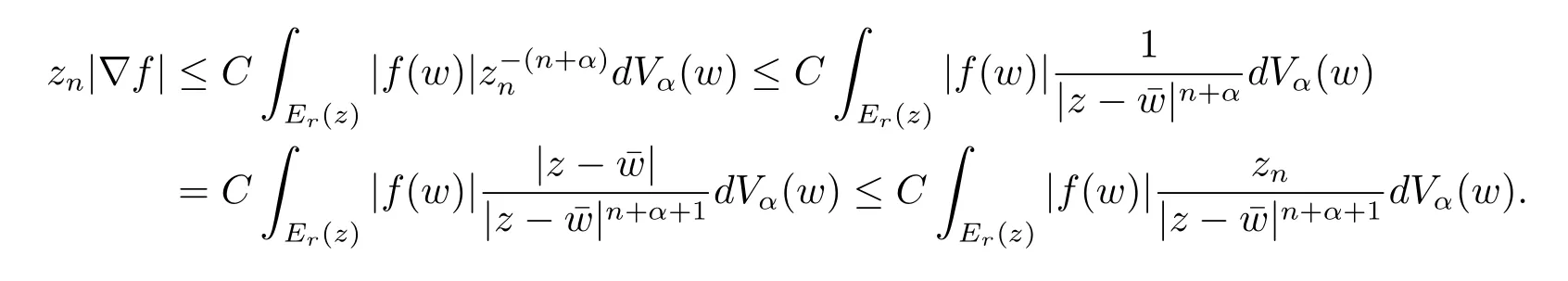
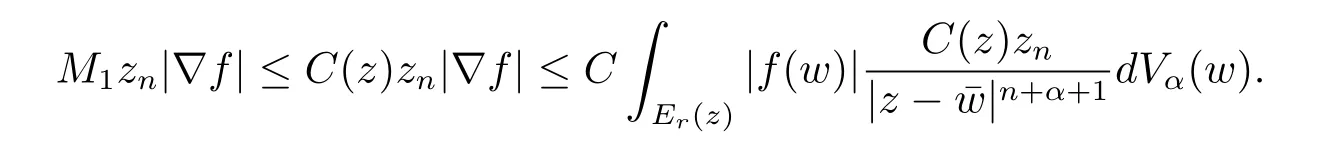
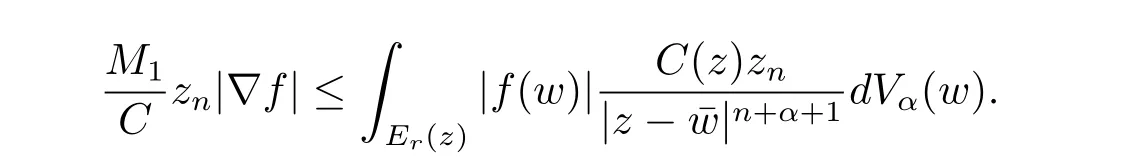
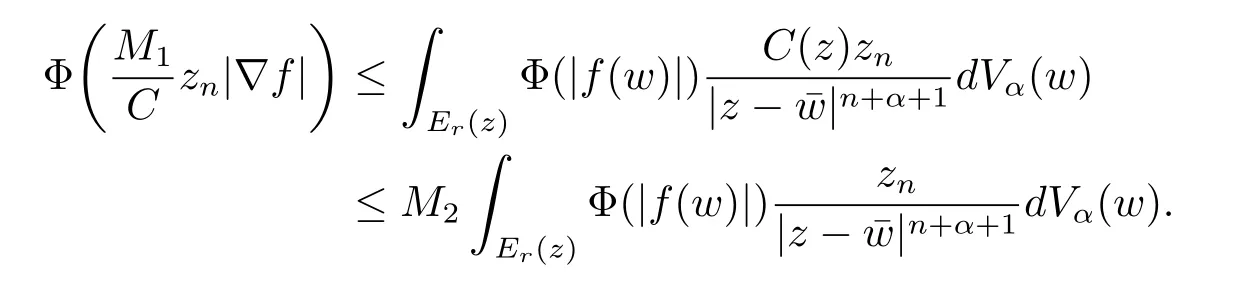
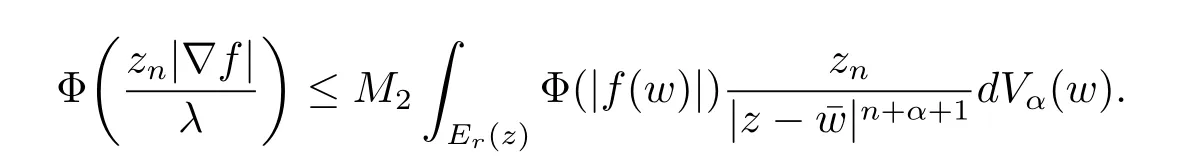
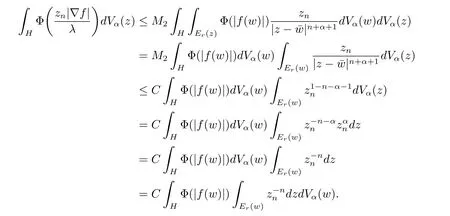

4 上半空間上調和函數的差商
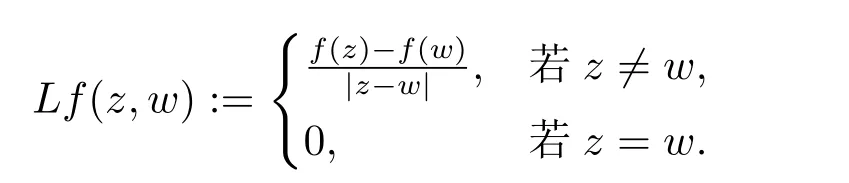
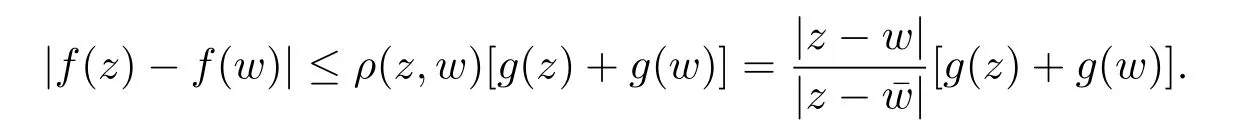
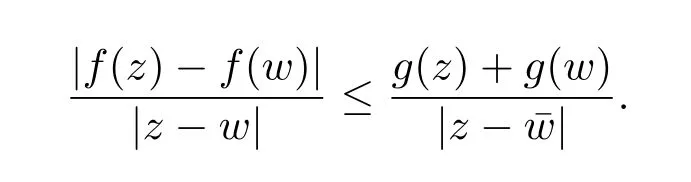
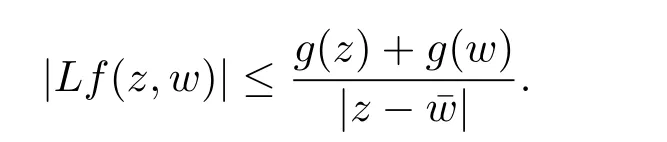
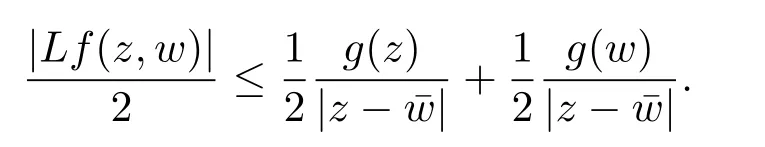
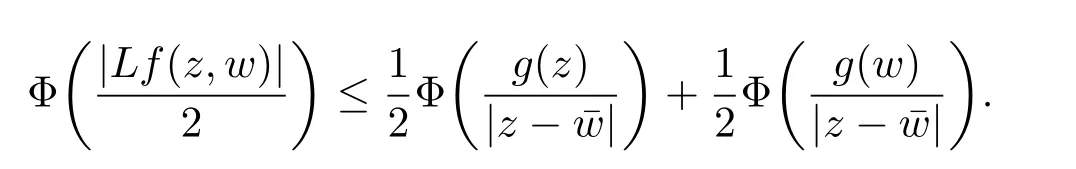
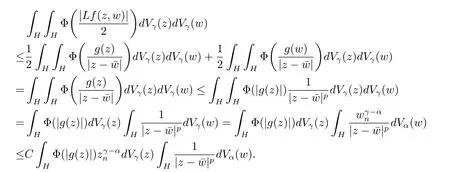
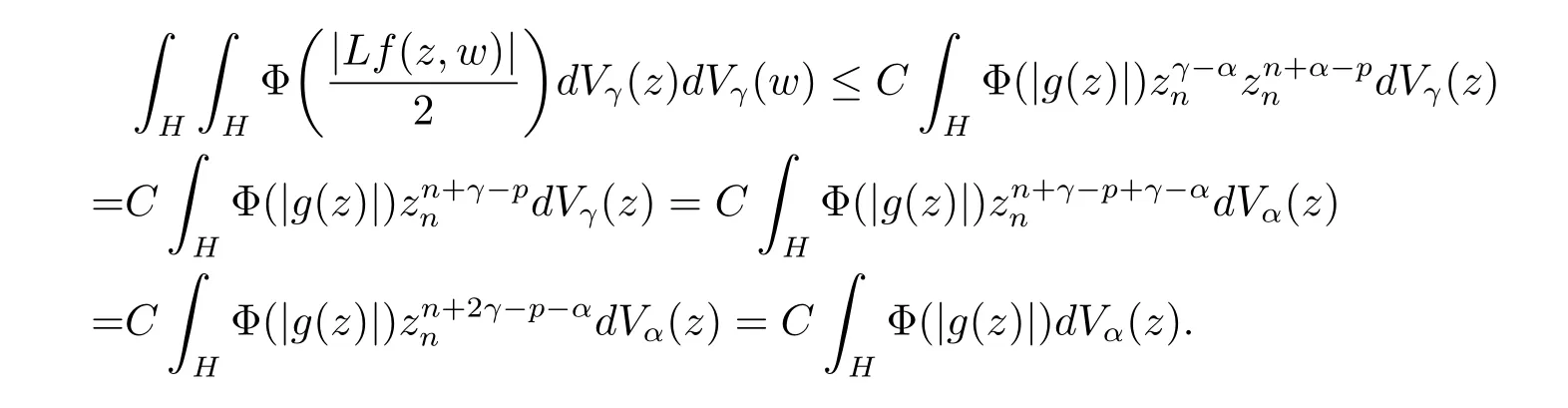
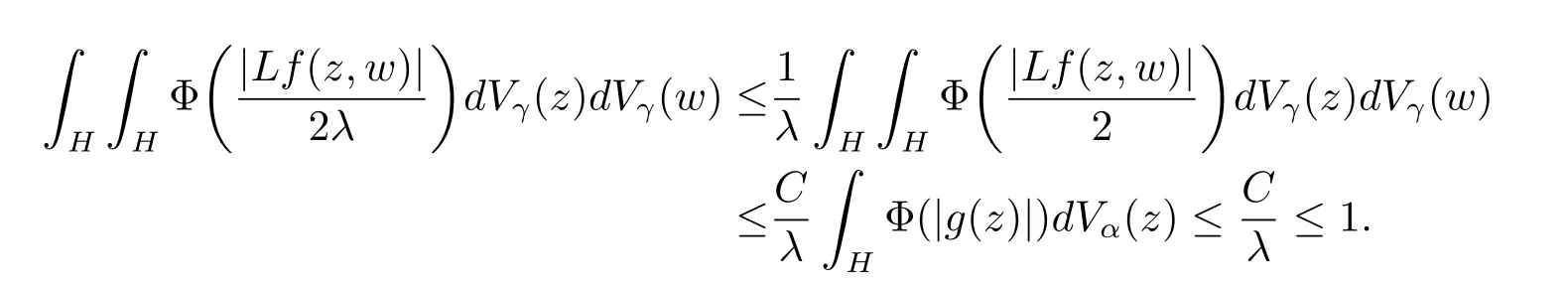
5 單位球上調和Bergman-Orlicz 空間的刻畫