求解廣義Fermat-Torricelli問題的多層鄰近梯度算法
馬麗麗,謝秋玲,胡清潔
(桂林電子科技大學 數學與計算科學學院,廣西 桂林 541004)
Fermat-Torricelli問題最初由法國數學家Pierre de Fermat提出,即給定平面上的3點,找到1個點,使其與3點的歐幾里德距離之和最小。這個問題引發了對位置科學的研究興趣,意大利數學家Evangelista·Torricelli最早研究該問題。隨后這個問題被稱為Fermat-Torricelli問題。該問題一直是優化領域中的一個研究熱點,在優化網絡[1]、設施選址[2]、計算幾何[3]、定位科學、物流等方面具有廣泛應用。l2范數下廣義Fermat-Torricelli問題模型為
(1)
其中:ai∈Rn,i=1,2,…,m;Ω為Rn上的非空閉凸集。集合的廣義Fermat-Torricelli問題模型為
(2)
其中:Ωi(i=1,2,…,m)為目標集。
近年來,Fermat-Torricelli問題得到廣泛關注。Weiszfeld[4]首次提出求解Fermat-Torricelli問題的算法,隨后,許多研究者對該算法進行了修正和改進[5-7]。Nam等[8]提出用Nesterov光滑技術求解廣義Fermat-Torricelli問題,其主要思想是對原目標函數構造光滑逼近,利用加速梯度法求解,并用數值實驗說明算法的有效性。Parpas等[9]基于多層優化方法,提出用多層加速梯度鏡面下降算法求解大規模人臉識別問題,并用數值實驗驗證了該算法的可行性。
為求解廣義Fermat-Torricelli問題,基于文獻[9-10],提出多層鄰近梯度算法,并給出相關收斂速度分析和數值實驗。
1 預備知識
定義1給定集合Ω?Rn,則
稱為集合Ω的示性函數。
定義2[8]點x到Rn上非空閉凸集Ω的歐式投影為
π(x;Ω)={w∈Ω|d(x;Ω)=‖x-w‖}。
特別地,點x到以δ為中心、r為半徑的立方體集合Ω上的投影為
PΩ(x)=max{δi-r,min{xi,δi+r}}。
2 算法描述
對模型(1)的目標函數進行μ光滑[11]和引入示性函數,則原問題可轉化為
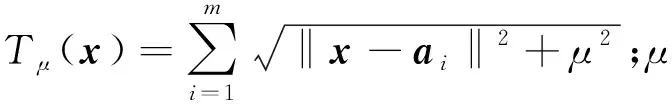
同樣地,模型(2)的問題可轉化為
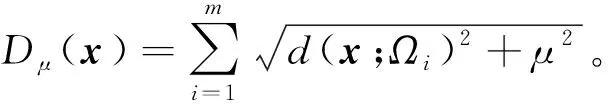
將上述2個問題的一般形式記為
(3)
其中:f:Rn→R為光滑凸函數;g:Rn→R為連續凸函數不一定光滑。
QL(x,y)=f(x)+〈y-x,f(x)〉+
定義PL(x)=argmin{QL(x,y),y∈Rn}。
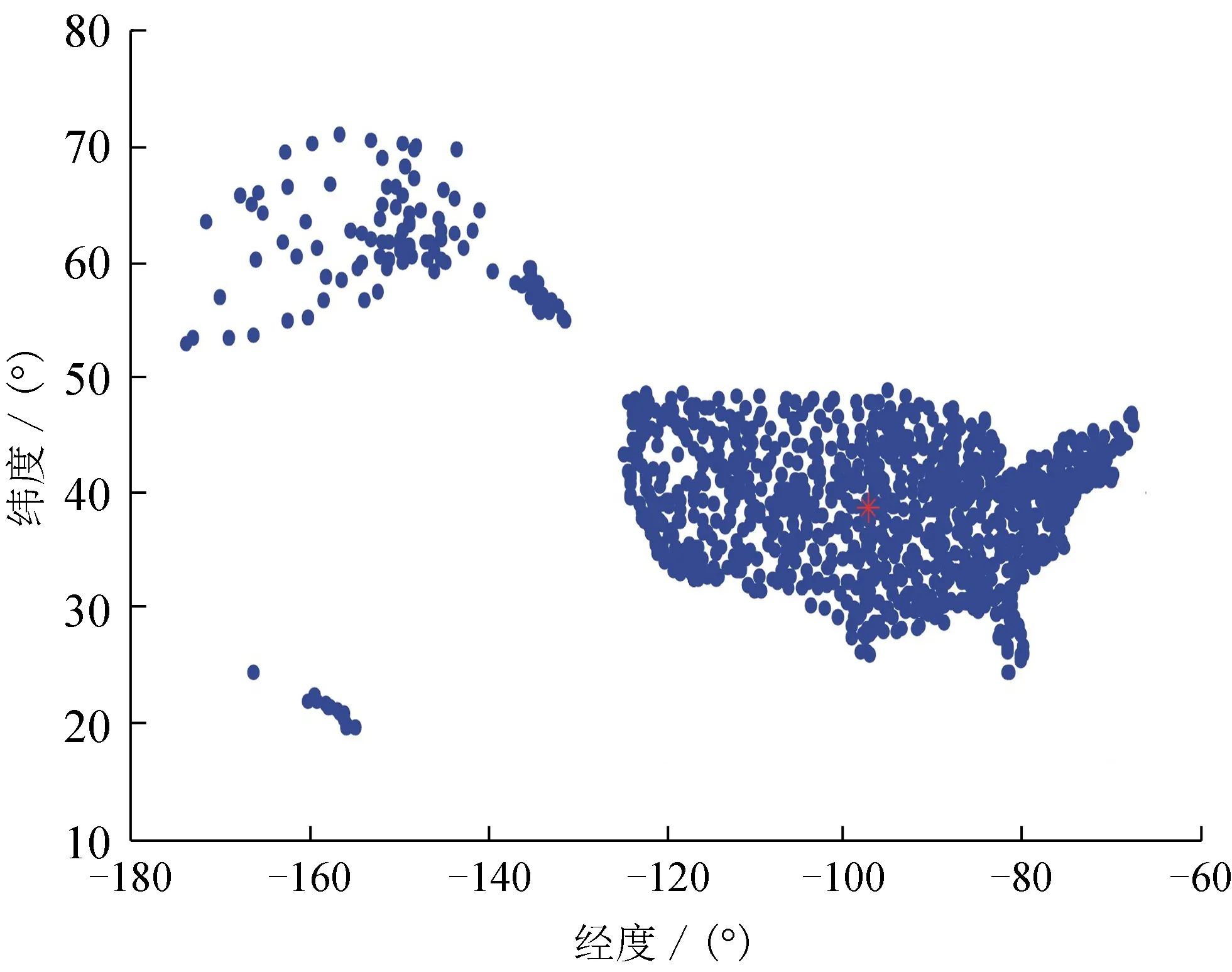
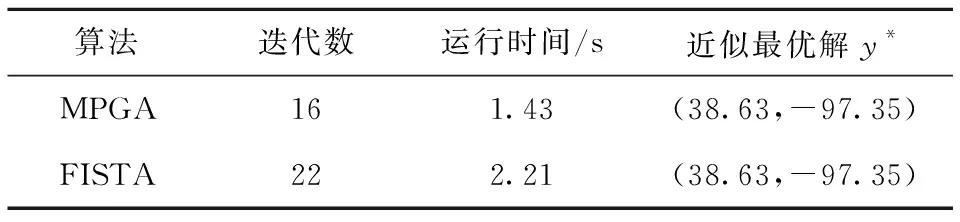
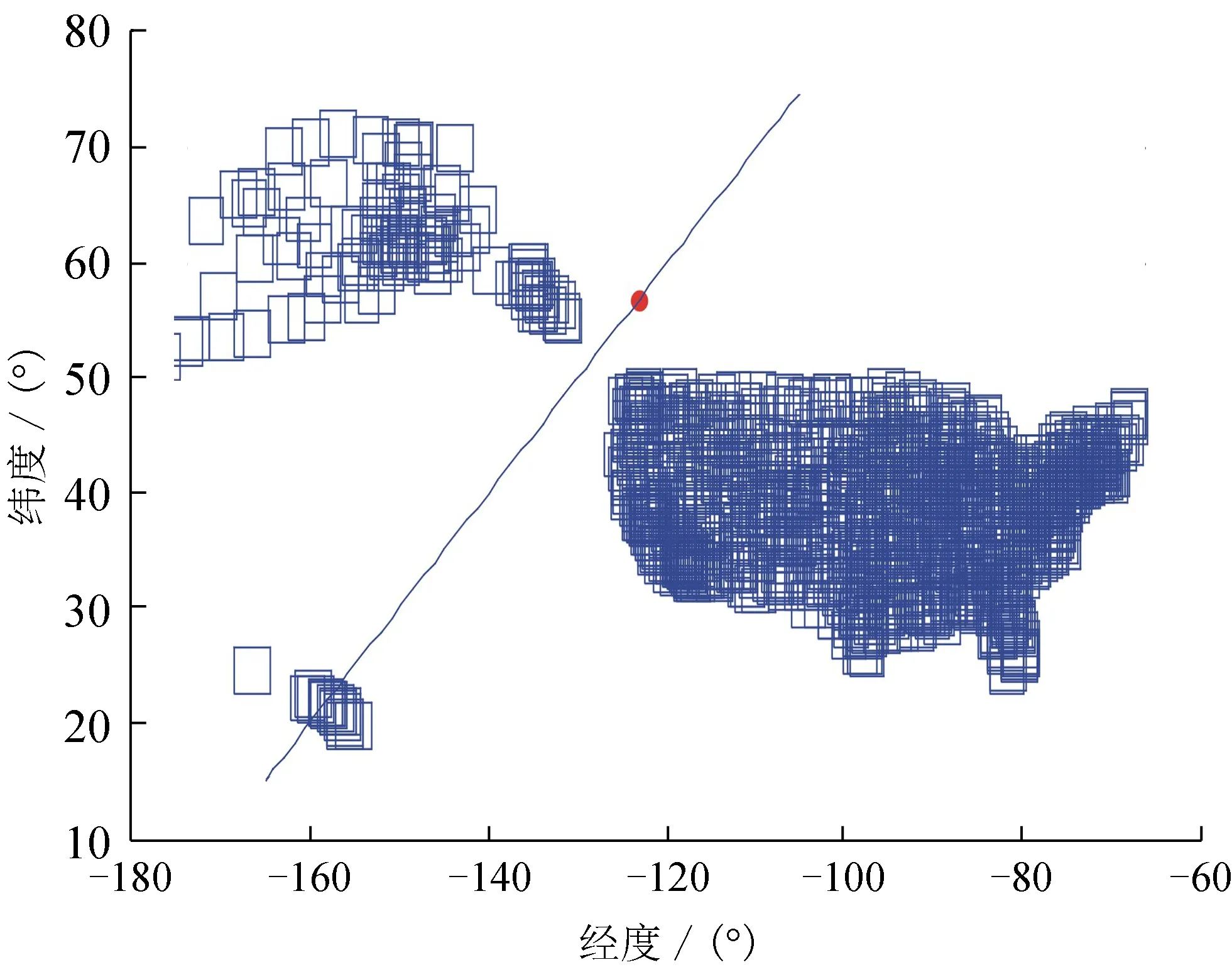
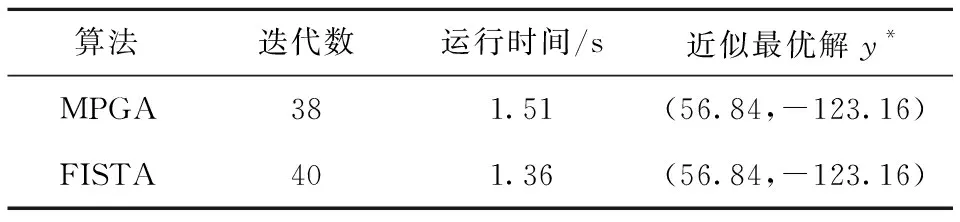
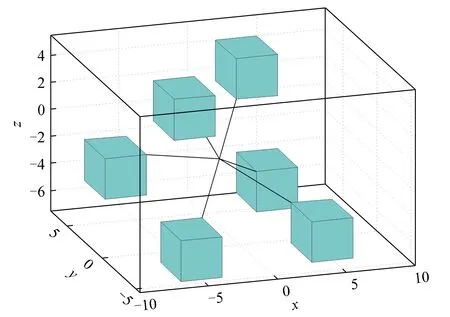
多層算法需要在層次之間使用適當的信息傳遞機制。為了在層次之間傳遞信息,引入線性限制算子R:Rn×nH和延拓算子P:RnH×n,其中nH σP=RT, 其中σ>0,不失一般性,假設σ=1。算子的選取參見文獻[12]。 為求解粗糙子問題,引入一個光滑參數ε>0,對g(x)進行光滑化得到gε(x),光滑后的目標函數為 Fε(x)=f(x)+gε(x)。 粗糙模型的關鍵屬性是初始點xH,0處2個模型的最優性條件相匹配,可通過在粗略模型的目標函數中引入線性項來實現。粗糙模型的目標函數為 FH,ε(xH)=fH(xH)+gH,ε(xH)+〈vH,xH〉。 其中:fH(xH)、gH,ε(xH)均為光滑函數;vH=RFε(x)-(fH(Rx)+gH,ε(Rx))。 迭代過程中,算法是否使用粗糙模型構建搜索方向取決于當前迭代點xk的最優性條件。進行粗糙迭代應滿足以下2個條件: (4) 為滿足相容性,用xH,0=Rxk開始粗糙迭代,通過一階優化方法求解粗糙模型并構造搜索方向, dk(xk)=P(xH,NH-Rxk), 其中xH,NH∈RnH為執行NH次迭代后粗糙模型的近似解。由于通常找不到精確解,利用Nesterov加速梯度算法[8]求解該子問題,得到一個可接受的解xH,NH。 多層鄰近梯度算法的步驟為: 1)選取L>0,τ>0,ε>0,0 2)若粗糙條件(4)不滿足,轉步驟3),否則執行NH次粗糙迭代得xH,NH,計算dk=P(xH,NH-Rxk)。由Armijo線搜索求得步長sk, Fε(xk+skdk)≤Fε(xk)+cskFε(xk)Tdk。 3)計算yk=PL(xk),若‖xk-yk‖<τ,迭代終止,輸出yk作為近似極小點,否則轉步驟4)。 為了分析多層鄰近梯度算法的收斂速度,首先給出如下4個引理。 引理1若x∈Rn,存在L>0,使得 Fε(PL(x))≤Q(PL(x),x) 成立,則對?y∈Rn,有 L〈x-y,PL(x)-x〉。 引理2設{xk}和{yk}是由多層鄰近梯度算法產生的序列,則對?k≥1,有 其中 vk=Fε(yk)-Fε(y*),uk=tkyk-(tk-1)yk-1-1。 2〈xk+1-yk,yk+1-xk+1〉。 (5) 2〈xk+1-y*,yk+1-xk+1〉。 (6) ‖tk+1(yk+1-xk+1)‖2+2tk+1× 〈tk+1xk+1-(tk+1-1)yk-y*,yk+1-xk+1〉= ‖tk+1yk+1-(tk+1-1)yk-y*‖2- ‖tk+1xk+1-(tk+1-1)yk-y*‖2= ‖tk+1yk+1-(tk+1-1)yk-y*‖2- ‖tkyk-(tk-1)yk-1-y*‖2。 由uk的定義得 引理得證。 引理3[10]設{ak}和{bk}都是正實數序列,假設對于?k≥1,a1+b1≤c,c>0,ak-ak+1≥bk+1-bk成立,則對?k≥1,ak≤c也成立。 引理4[10]設{tk}是由多層鄰近梯度算法產生的序列,且t1=1,則對?k≥1,tk≥(k+1)/2成立。 基于上述4個引理,估計該算法的收斂速度。 定理1設{yk}是由多層鄰近梯度算法產生的序列,則對?k≥1,a1+b1≤c,c>0,有 Fε(y*)-Fε(y1)=Fε(y*)-Fε(PL(y1))≥ 等價于 ‖y1-y*‖2-‖x1-y*‖2。 即a1+b1≤c成立,由引理2得ak-ak+1≥bk+1-bk成立,由引理3得 從而可得 定理得證。 為檢驗算法的有效性,考慮文獻[8]的數值算例,采用Matlab編制程序,其測試環境為Window 10操作系統,Intel (R) Core (TM) i5-6500 CPU @ 3.20 GHz,8.00 GB RAM。 算例1給定1217個美國城市的經緯度,其數據可從文獻[8]提供的網址找到。為更符合實際分布情況,將其經度乘以-1由正轉負。現在需要找到一個點,使得該點到給定美國城市點的距離之和最小。選取初始點y0=(20,-100),限制算子R=[1/4 1/2],粗糙參數η=0.2,θ=0.8,M=30,利普希茨常數L=70,精度τ=10-5,得到近似最優解y*≈(38.63,-97.35)。美國各城市及其最優點的分布結果如圖1所示。將多層鄰近梯度算法(MPGA)與迭代收縮閾值算法(FISTA)算法進行比較,結果如表1所示。從表1可看出,在相同的初始值和最優解達到相同精度時,多層鄰近梯度算法迭代次數和運行時間較少。 圖1 美國城市及其最優點的分布結果圖 算法迭代數運行時間/s近似最優解y*MPGA161.43(38.63,-97.35)FISTA222.21(38.63,-97.35) 算例2與算例1的設置相同,以上述1217個美國城市為中心點,半徑r=1.5的1217個正方形,現在需要在直線x-y=180上找到一個點,使得該點到1217個正方形的距離之和最小。選取初始點y0=(0,180),其他參數的選取同算例1,最后得到近似最優解y*≈(56.84,-123.16),各廣場及其最優點的分布結果如圖2所示。將多層臨近梯度算法(MPGA)與迭代收縮閾值算法(FISTA)進行比較,結果如表2所示。從表2可看出,在相同的初始值和最優解達到相同精度時,多層鄰近梯度算法迭代次數較少,但運行時間略多于FISTA算法。 圖2 美國廣場及其最優點的分布結果圖 算法迭代數運行時間/s近似最優解y*MPGA381.51(56.84,-123.16)FISTA401.36(56.84,-123.16) 算例3考慮以(-6,6,-4),(-5,-3,-6),(2,3,4),(4,-4,-5),(5,6,-6),(-5,-2,4)六個點為中心,半徑r=1.5的6個正方體,現在需要找到一個點,使得該點到6個正方體的距離之和最小。選取初始點y0=(-6,6,2),限制算子R=[1/4 1/2 1/4],粗糙參數和精度的選取與算例1相同,利普希茨常數L=0.8,得到近似最優解y*≈(-1.040 5,0.840 2,-1.432 2),正方體及其最優點的分布結果如圖3所示。將多層鄰近梯度算法(MPGA)與迭代收縮閾值算法(FISTA)進行比較,結果如表3所示。從表3可看出,在相同的初始值和最優解達到相同精度時,多層鄰近梯度算法迭代次數和運行時間較少。 圖3 正方體及其最優點的分布結果圖 算法迭代數運行時間/s近似最優解y*MPGA110.027 6(-1.040 5,0.840 2,-1.432 2)FISTA160.028 1(-1.040 5,0.802 4,-1.432 2) 針對點和集合的廣義Fermat-Torricelli問題,提出一種多層鄰近梯度算法,采用μ光滑方法將原始目標函數轉化為光滑函數,再利用多層鄰近梯度算法求解,并從理論上證明該算法具有O(1/k2)的收斂速度。數值實驗表明,多層鄰近梯度算法求解廣義Fermat-Torricelli問題是有效的。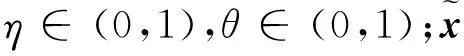
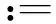
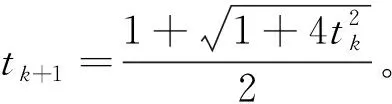
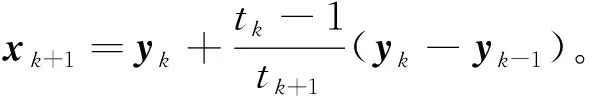
3 收斂速度分析

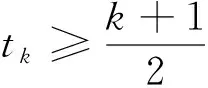
4 數值實驗

5 結束語

