基于多項式預處理的特殊雙變量矩陣方程異類約束解算法
周咸富,段復建
(桂林電子科技大學 數學與計算科學學院,廣西 桂林 541004)
討論一類特殊的雙變量矩陣方程
AXB+AYB=F
(1)
的異類約束解加速問題,其中A,B,F∈Rn×n,X∈Rn×n,Y∈SRn×n,且A、B是對稱正定矩陣。對于方程(1)的研究,不同約束條件可用不同的方法,一般采用共軛梯度法求解。劉莉[1]利用共軛梯度法求矩陣方程AXB+CYD=E的中心對稱最小二乘解;方玲等[2]利用極小殘差法求解AXB+CYD=E的對稱最小二乘解。但這些方法迭代過程中的收斂性不確定,即便收斂,收斂速度也較慢。針對收斂速度慢的問題,進行預處理是提高收斂速度的主要途徑之一。Zhao等[3]提出了一種基于參數迭代預處理方法和共軛梯度修正形式(MCG)相結合的并行預條件求解算法;溫瑞萍等[4]提出了不完全SAOR預條件共軛梯度法;Jia等[5]提出了一種基于殘差的稀疏近似反預處理方法。對于矩陣方程異類約束解問題,李書連等[6]通過修改系數矩陣和其方向,提出了修正共軛梯度算法,解決了雙變量矩陣方程組最小二乘問題;牛婷婷等[7]將多變量異類約束問題推廣到一類離散時間代數Riccati矩陣方程,建立了雙迭代算法;宋衛紅等[8]利用逆矩陣的Neumann級數形式,將多變量異類約束解推廣到離散對偶代數Riccati矩陣方程,構造了雙迭代算法。
預處理方法大多應用于解同類線性方程組,用于雙變量矩陣方程異類約束條件的研究不多,且對于異類約束的矩陣方程收斂速度的研究也不多見。因此,將多項式預處理[9]和共軛梯度法相結合,提出多項式預處理共軛梯度法。
1 多項式預處理技術
定義同階對稱正定矩陣A與B的內積為[A,B]=tr(ATB),由此導出的Frobenius范數為
設Rn×n為n×n階矩陣集合,SRn×n為n×n階對稱矩陣集合,σ為A的任意奇異值,S=[a,b]為σ的取值區間,a和b分別為σ的最小與最大奇異值,τ為B的任意奇異值,L=[d,e]為τ的取值區間,d和e分別為λ的最小、最大奇異值。
迭代法求解矩陣方程,收斂速度與系數矩陣奇異值的分布有關。奇異值分布越集中,條件數越接近于1,收斂速度越快,反之,則會很慢。利用多項式對矩陣方程進行預處理,可使其奇異值的分布相對集中,條件數接近于1,從而提高收斂速度。
對矩陣方程AXB+AYB=F作等價變換
C(A)AXBC(B)+C(A)AYBC(B)=C(A)FC(B),
(2)
其中C(A)、C(B)為次數小于n的實系數多項式矩陣。若C(A)A和C(B)B的譜條件遠遠小于A、B的譜條件數,則利用共軛梯度法求解式(2)的收斂速度將大大快于直接求式(1)的收斂速度。所以選取系數多項式時,應使C(A)和C(B)在某種意義下接近A-1和B-1,這樣經過處理后的迭代次數遠比之前少。若A或B的最大奇異值和最小奇異值相差不大,則不需要進行預處理。令
F(A)=C(A)A,G(B)=BC(B),
Q=C(A)FC(B),
則式(1)的求解問題等價于
F(A)XG(B)+F(A)YG(B)=Q
(3)
的求解。
由多項式插值原理可得A的預處理多項式:
(4)
(5)
(6)
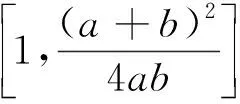
a≤σi≤b,i=1,2,…,n,
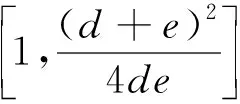
d≤τi≤e,i=1,2,…,n,
定義1設A∈Rn×n,A為非奇異矩陣,‖·‖為定義在Rn×n上的范數矩陣,稱
cond(A)v=‖A-1‖v‖A‖v,v=1,2,or,∞
為A關于范數‖·‖的條件數。
通常情況下,若矩陣A的條件數大,則稱A為病態矩陣,反之稱為良態矩陣,條件數越趨近于1,則越穩定。
采用最常見的Frobenius范數反映矩陣病態性,
當A為實對稱矩陣時,有
其中λmax、λmin分別為矩陣A最大、最小特征值。
定理1設式(1)中系數的譜條件數較大,經過一次多項式預處理后,得到新的矩陣方程最小與最大奇異值比值比原方程最小與最大奇異值比值提高16倍。
證明設經過一次插值多項式預條件,得到C(A)A的最小、最大特征值分別為a′、b′,C(B)B的最小、最大特征值分別為d′、e′。記
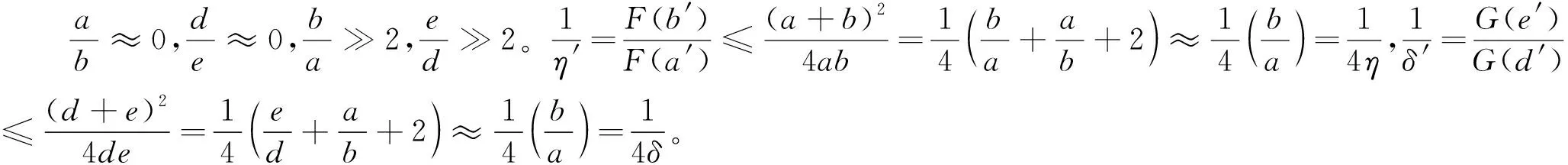
2 多項式預處理共軛梯度算法
對于方程(1)用共軛梯度法求解,若條件數遠大于1,則收斂速度較慢。為了提高收斂速度,引入多項式預處理技術構造新的算法。
算法1定義1+ε1,1+ε2,(ε1>0,ε2>0)分別為系數矩陣A、B的非零最大、最小奇異值比值的滿意的臨界值。
1)給出初始解X0∈Rn×n、Y0∈SRn×n和初始邊界a0、b0、d0、e0。
2)對于i=0,1,…,n,求矩陣多項式:
3)若bi/ai≤1+ε,ei/di≤1+ε2,則停止預處理,轉步驟5),否則,令
Ai+1=F(Ai),
Bi+1=G(Bi),
Qi+1=C(Ai)FC(Bi)。
4)計算ai+1=1,bi+1=(ai+bi)2/4aibi,di+1=1,ei+1=(di+ei)2/4diei,轉步驟2),i=i+1。
5)令
F(A)=F(Ai),G(B)=G(Bi),Q=Qi+1。
6)計算
R0=Q-(F(A)X0G(B)+F(A)Y0G(B)),
P0=FT(A)R0GT(B),
U0=P0,
V0=Q0,k=0。
7)若Rk=0,或Rk≠0,而‖Uk‖2+‖Vk‖2=0,停止,否則,k=k+1。
8)計算
Xk=Xk-1+αk-1Uk-1,
Yk=Yk-1+αk-1Vk-1,
Rk=Q-(F(A)XkG(B)+F(A)YkG(B))。
9)計算
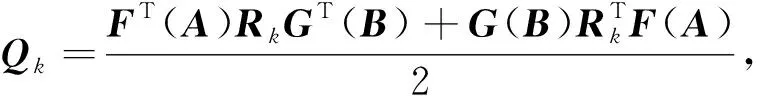
10)轉步驟8)。
需要注意的是,在實際求解中,系數矩陣的最大與最小奇異值很難求出,因此,利用上述算法在求解C(A)、C(B)時,對于a0、b0、d0、e0可利用合適的估計式,
對于算法1,一般都有以下2個性質。
性質1若矩陣方程(3)是相容的,算法中{Ri}、{Ui}、{Vi}滿足以下關系:
〈Ri,Rj〉=0, 〈Ui,Uj〉+〈Vi,Vj〉=0,
其中i,j=1,2,…,k,i≠j。
性質2若線性方程(1)是相容的,且[X*,Y*]是其一個解,則對于任意初始矩陣對[X0,Y0],算法中的迭代序列{Xi}、{Yi}、{Ri}、{Pi}、{Qi}、{Ui}、{Vi}滿足如下關系:
其中i=1,2,…,k-1。
定理2若矩陣方程(1)有解,則對任意選定的初始迭代矩陣對[X1,Y1],應用算法1,矩陣方程(1)異類約束解可經過有限步迭代得到。
證明若Ri≠0,i=1,2,…,pq,由性質2可得‖Ui‖2+‖Vi‖2≠0。根據算法1,由迭代計算可得Rpq+1、Upq+1、Vpq+1,且由性質1知
〈Rpq+1,Ri〉=0, 〈Ri,Rj〉=0,
其中i,j=1,2,…,pq,i≠j。序列{Ri}構成了矩陣空間Rp×q的一個正交基,故Rpq+1=0,即Xpq+1、Ypq+1為方程的一個解。
引理1設算法產生的迭代序列{Xk}在某種范數意義下收斂,
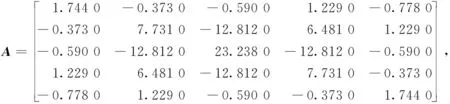
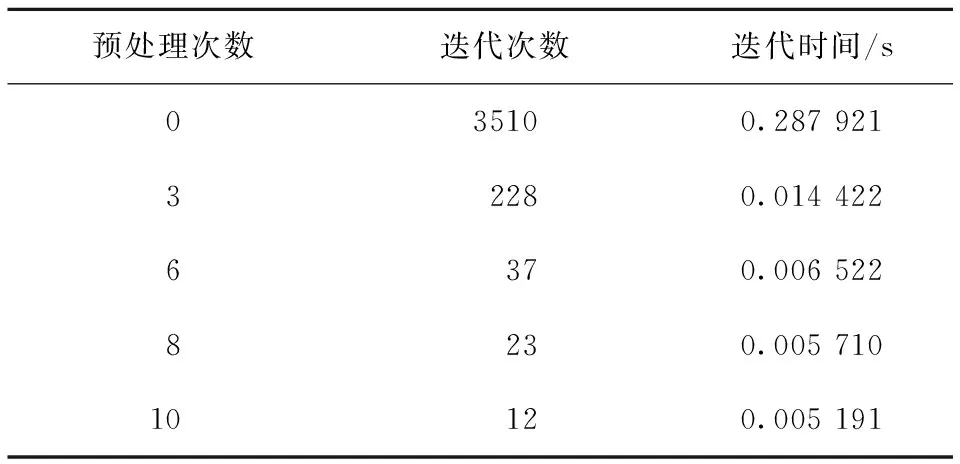
若存在實數α>0和一個與迭代次數無關的常數0 ‖Xk+1-X*‖=q‖Xk-X*‖α, 則稱算法產生的迭代序列{Xk}具有Q-α階收斂速度。特別地,當α=1,0 為證明多項式預處理共軛梯度法產生的迭代序列{Xk}、{Yk}具有Q-線性收斂速度,作如下變換。 記Mk=Xk-X*,Nk=Yk-Y*,則Mk+1=Mk+αkUk,Nk+1=Nk+αkVk,即 且由性質2可知,對任意的i≠k,有 (7) (8) 結合算法1,經過計算證明,產生的序列{Mk}、{Nk}具有如下結論。 性質3對k≥1,有 (9) (10) 證明由式(7)、(8)可得 tr((Mk+αkUk)T(Mk+αkUk))+ tr((Nk+αkVk)T(Nk+αkVk))= 2αk‖Rk‖2=‖Mk‖2+‖Nk‖2+ (‖Uk‖2+‖Vk‖2)= 定理3設迭代序列{Xk}、{Yk}由多項式預處理共軛梯度算法經過0次預處理產生,且A、B為對稱正定矩陣,則有 (11) 其中X*、Y*是方程(1)的解,σn=a,σ1=b,τq=d,τ1=e分別是A、B的最小、最大奇異值。 證明假定A、B的奇異值分解為 A=UΣVT,B=WDTT。 (12) 其中:U、V、W、T皆為正交矩陣; 且 b=σ1≥σ2≥…≥σn=a, e=τ1≥τ2≥…≥τq=d。 由式(10)、(12)可得, ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2≤ 即有 定理4多項式預處理共軛梯度算法經過一次預處理后的Q-收斂速度為 證明由定理1知,經過一次預處理,最小與最大奇異值比值提高了16倍,結合定理3可得結論,證畢。 已知矩陣A,B,F∈R5×5,且A、B是對稱正定矩陣,求X∈R5×5,Y∈SR5×5,使 AXB+AYB=F。 X0=zeros(5), Y0=zeros(5)。 其中A的最大和最小奇異值分別為b=37.436 0,a=0.024 0,B的最大和最小奇異值分別為e=97.310 1,d=0.025 1。 使用共軛梯度迭代法進行求解,在迭代過程中,取ε=1×10-8作為迭代終止條件,即當‖Rk‖<ε,迭代停止。對于本例,可以求得如下結果: 迭代次數k=3 510,迭代時間t=0.287 921 s,誤差‖R3 510‖=6.637 3×10-9<ε。 利用多項式預處理共軛梯度算法,求解AXB+AYB=F。同樣的迭代終止條件,本算法的迭代結果如表1所示。從表1可看出,預處理次數i=10,迭代次數k=12,迭代時間t=0.005 191 s,本算法比共軛梯度法迭代次數減少了3 498,迭代時間縮短了0.282 730 s。 表1 本算法的迭代結果 基于共軛梯度算法,引入多項式預處理技術,構造了多項式預處理共軛梯度算法,并用于求解特殊雙變量矩陣方程異類約束的問題,同時證明了該算法是收斂,且具有Q-線性收斂速度。數值實驗表明,多項式預處理共軛梯度算法比共軛梯度算法收斂速度更快,需要的迭代時間更短,且算法是有效、可行的。
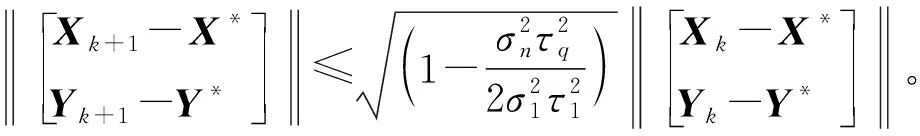
3 數值實驗




4 結束語

