在初中數學課堂教學中夯實建模過程的分析
王書文
摘要:“數學就是對模式的研究”,而在初中數學課堂教學中夯實建模過程就是要引導學生學數學、做數學、用數學,從而提高學生建模能力,發展其數學應用意識,提高學生數學素質。本文從立足教材,分層次滲透數學建模,重視數學知識產生和發展過程數學建模思想,注重數學建模的活動性等方面分析在初中數學課堂教學中夯實建模過程的實踐。
關鍵詞:建模過程;初中數學;課堂教學
中圖分類號:G633.6文獻標識碼:A文章編號:1992-7711(2019)10-043-1
數學建模過程是一個由淺入深發展學生數學思維的過程,數學建模教學的目的就是要讓學生學習數學,應用數學,形成運用數學思維解決實際問題的能力。初中數學教師應將數學建模與課堂教學融為一體,夯實建模過程,讓學生學會通過數學建模學習數學,將其作為提升數學素養的最佳途徑,提高學生數學學習能力[1]。
一、立足教材,在課堂教學中分層次滲透數學建模
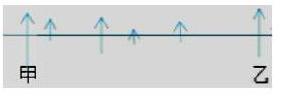
在初中數學教學之初,教師就要重視對學生建模能力的培養,在日常課堂教學中夯實建模過程,引入現實生活問題,聯系相關數學知識,促進數學課堂教學生活化。初中數學教師要深入研究教材,將教材和數學建模教學有機統一,探究各個章節中應該引入什么模型問題,在課堂教學中貫穿數學建模意識。教師要注意從學生生活中引入數學知識,從而讓學生發現生活問題,進而帶著問題走進課堂,為數學知識構建生活原型。在初中數學學習中,學生通常要建立幾何圖形模型、操作探究型、閱讀理解型、方程或不等式模型、三角函數模型、函數模型等,來解決應用問題,因此教師要分層次逐步滲透數學建模[2]。例如:建立幾何圖形模型。如題1:火車往返甲、乙兩地,中途會停靠4個車站,請問需要設計多少種不同票價,要準備多少種火車票?在這一問題中,可以將車站、停靠點作為一條直線上的6個點,根據路程長短而變化票價,票價的總數就是圖中不同線段的總數乘以2倍,這是要考慮到火車往返時起始站和終點站發生變化的緣故。
二、重視數學知識產生和發展過程中的數學建模思想
在數學知識產生和發展過程中,蘊含著豐富且明顯的數學建模思想,因此在初中數學課堂教學中,教師要有意識引導學生重視探究數學知識產生和發展過程,從中自然構建數學建模意識,感受數學建模思想,讓學生學會從數學角度發現問題,提出問題,理解問題,并運用數學知識和數學思想解決問題。教師要強調從運算意義出發進行教學,并與學生生活密切相連,創造生活化的教學情境,讓學生在情境探究數學知識的過程中,經歷完整構建數學模型的過程,起到夯實建模過程的目的[3]。
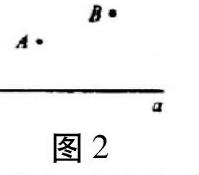
如題2:果林和王村在河流一邊,現要在河邊修建水泵站,以方便向果林和王村送水,請問修在河邊什么地方最佳?
根據題目分析建模過程,首先將河流抽象為直線,兩地點分別為A、B點,構建如圖2的幾何圖形模型。
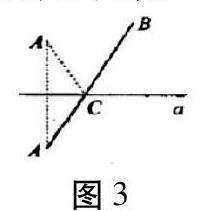
然后探索問題,最佳修建水泵站的地方是指到兩地直線距離最近,使得修建水管更短,從而減少人力、物力消耗。教師可引導學生由此聯想到“兩點間線段最短”等知識,然后虛擬水泵C點,探究C點在哪時AC與BC之和最小,畫出如下幾何圖形模型,并通過轉化已學過的軸對稱圖形及性質相關知識,使得AC+BC成為一條線段(圖3),自然可得出答案。
通過這些生活化情境,讓學生多經歷完整的數學建模過程,從而持續地培養學生數學應用意識、建模意識,讓學生逐漸掌握數學建模的方法,使得學生能利用數學建模途徑更好地學習數學知識。在初中數學課堂教學中,教師要強調過程的重要性,重視實際問題背景的分析,重視分析數學模型建立的過程,從而真正落實提高學生數學建模能力的教學目的。
三、注重數學建模的活動性
在初中數學課堂教學中,夯實數學建模過程,培養學生數學應用意識不僅僅是指讓學生解決一些具體問題,而是為了擴充學生數學知識,提高學生數學素質,促進學生從知識型轉化為能力型,改變以往的被動學習狀態。因此,在課堂教學中,教師要改變傳統“老師講題、學生模仿練習”的教學模式,注重數學建模的活動性,在課堂探究活動中夯實建模過程,引導學生主動參與活動,重視探究過程,從而提高學生的建模能力[4]。例如:在《三角形》一課教學中,教師可以提出如下問題:池塘(圖4)兩端記為AB,不進入池塘內要測量兩端點距離,有什么好辦法?
將學生分組,讓學生通過討論,模擬實驗等活動探究測量方式,并構建相應模型。如構造直角三角形,利用勾股定理解決問題;構造等邊三角形;構造兩個全等三角形等,鼓勵學生參與其中,大膽提出建模方法,獲得學習成功體驗。
四、結語
總之,在初中數學課堂教學中,教師要注重夯實建模過程,讓學生積極參與數學建模活動,通過構建數學模型,探究數學知識,培養學生數學應用意識,提高學生數學素質。
[參考文獻]
[1]溫春建.加強初中數學建模教學,培養學生應用數學意識[J].新課程導學,2015,10(35):101-102.
[2]張瑩瑩.數學建模在初中數學教學中的淺探[J].中學時代,2013,11(2):139.
[3]施娟.在初中數學課堂教學中夯實建模過程[J].數理化解題研究,2017,12(29):25-26.
[4]楊柳.在中學數學教學環節中滲透數學建模思想的思考——以平面直角坐標系為例[J].課程教育研究,2015,13(33):178-179.

