含非線性大變形構件的柔順機構建模與分析

李鵬飛， 曹博宇， 汪振宇， 趙 晨， 王立鵬

(西安理工大學 機械與精密儀器工程學院， 西安 710048)

傳統剛性機構借助于剛性構件和運動副實現運動和功能。柔順機構則是一種利用構件自身彈性變形完成運動和力傳遞及轉換的新型機構[1],具有減少構件數量和裝配時間、簡化加工工序、無摩擦磨損和傳動間隙、降低振動和噪聲等優點[2]，可應用于精密測量與定位、微機電系統(MEMS)、仿生機械、醫療器械等領域[3]。柔順機構運動往往伴隨著柔性構件的非線性大變形過程，須用非線性方程描述構件大變形造成的幾何非線性，使得柔順機構建模變得困難。

目前柔順機構的建模方法主要有偽剛體模型法[4-5]、橢圓積分法[6-7]和有限元法[8]等，其中偽剛體模型法和橢圓積分法較為常用，計算效率較高。偽剛體模型法將柔順桿件離散成為用扭簧鉸接的剛性桿件，柔順機構建模問題轉化為剛性機構建模，這種轉化是一種近似的轉化，誤差較大。Zhang等通過引入梁上拐點個數和梁末端彎矩方向等參數，運用橢圓積分法求解了梁在各種不同載荷條件下的大變形問題。王雯靜等基于有限元法建立柔順機構的動力學方程，但其梁單元基于小變形假設，對于描述大變形柔順機構具有一定的局限性。Berzeri等[9]應用ANCF法分析了具有大變形構件的平面四桿機構。

本文簡要介紹了橢圓積分法和ANCF法的基本原理，在比較兩種方法建模過程基礎上，對一種固定—導向柔順梁的變形過程和受力進行仿真，設計實驗裝置，驗證梁變形仿真結果的正確性。應用ANCF法對一種復雜柔順雙穩態機構進行建模分析，對比分析兩種建模方法的特點。

1 柔順機構建模

1.1 橢圓積分法基本原理

在現有的柔順機構建模方法中，常用橢圓積分法計算梁的大撓度變形。圖1所示為長度為L的懸臂梁在初始水平(虛線位置)、末端同時受到水平方向力Fx、豎直方向力Fy和彎矩MO共同作用時的變形示意圖，坐標系xOy如圖所示。根據Euler-Bernoulli梁理論，梁上任意一點A(x,y)處的彎矩M為

(1)

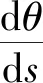
根據式(1)，可以推導得到最基本的橢圓積分法大撓度梁的支配方程為

(2)

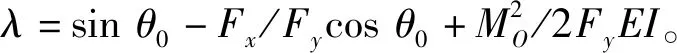
式(2)中忽略了梁的軸向變形以及截面的剪切作用。通過橢圓積分求解式(2)時，需先假定梁上拐點的個數和梁末端受到的彎矩方向，會出現多解，且對未知數的求解次序有一定的要求，不便于計算求解。

1.2 ANCF法基本原理

1.2.1 ANCF有限單元

ANCF法推導建立的多體系統微分代數方程具有常數質量矩陣、不存在科氏力和離心力項等特點，適合于描述大轉動大位移、大變形柔性多體系統。

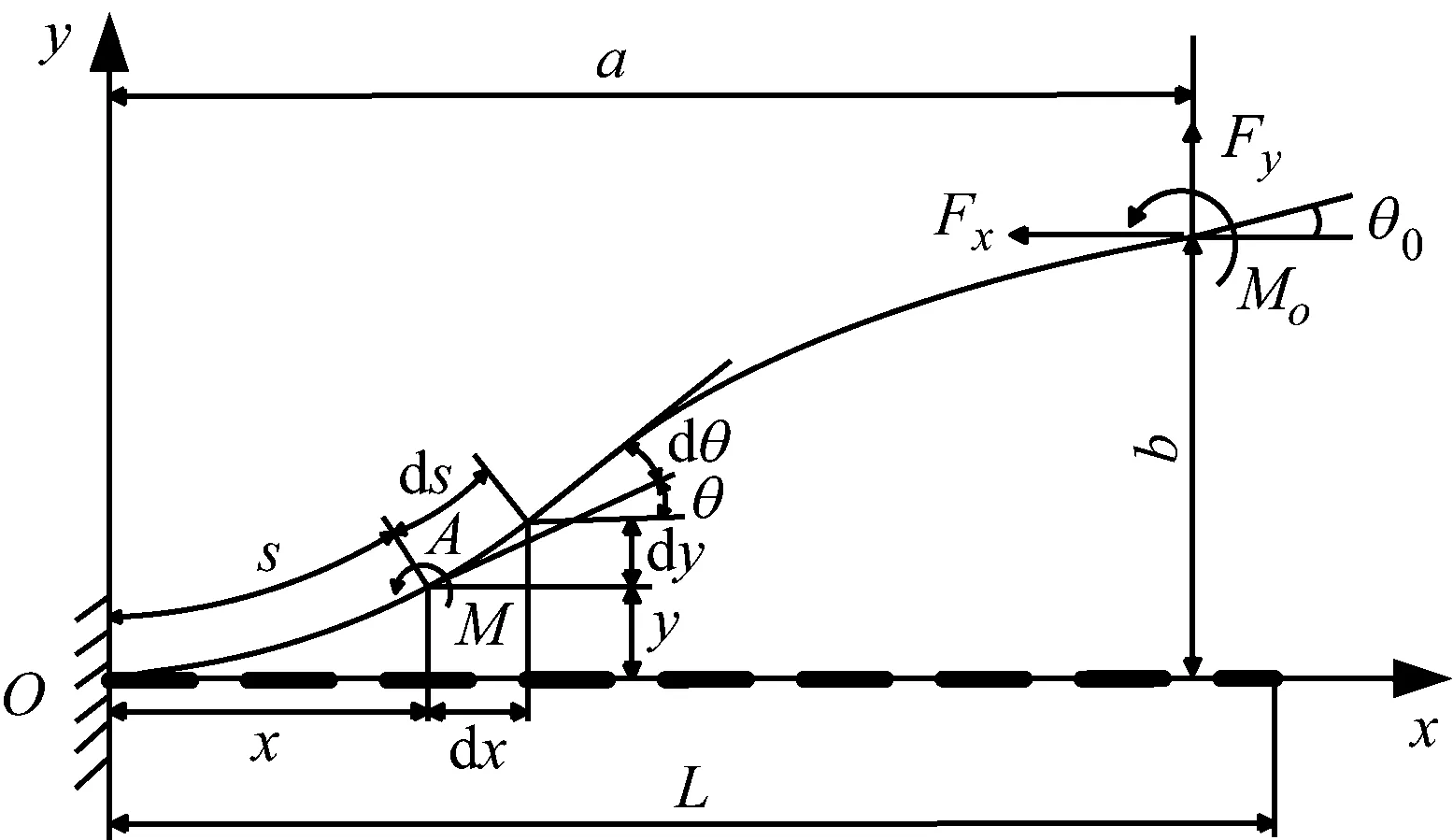
圖1 末端受力和彎矩作用的懸臂梁變形示意圖

如圖2所示，將柔順機構構件離散為三維二節點梁單元，該梁單元上任意一點的全局位置表示為[11-12]

r=S(x,y,z)e(t)

(3)

式中:S為單元形函數矩陣;e為單元節點坐標向量。

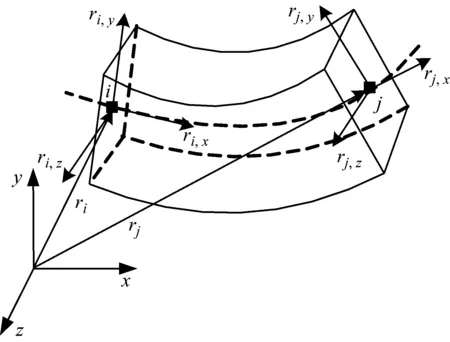
圖2 三維二節點梁單元

每個梁單元含有2個節點i、j，每個節點有12個絕對坐標，節點坐標e(t)定義為

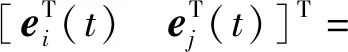
(4)

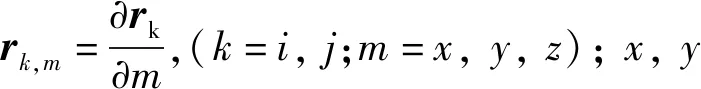
1.2.2 單元動力學方程

將式(3)對時間求導，由單元的動能表達式可寫出單元質量矩陣Me為

(5)

式中:ρ為材料密度;V為單元體積。

根據連續介質力學中非線性應變-位移關系可計算單元的廣義彈性力。變形梯度J寫為

(6)

式中:J0=?X/?x;X=Se0;x=[x，y，z]T，e0為單元初始位置時的節點坐標向量。則Green-Lagrange應變張量εm寫為

(7)

式中:張量εm包含梁單元的軸向拉壓、扭轉、彎曲應變以及截面的剪切作用;I表示單位矩陣。考慮到應變張量εm的對稱性，將其各元素寫為向量形式ε。由應變向量ε和應力向量σ間關系可以求出單元的應變能為

(8)

將應變能U對節點坐標e求偏導，可獲得彈性力向量

(9)

由式(5)、(9)，無約束條件下梁單元的動力學方程為

(10)

式中，Qe為單元外力向量。

將單元動力學方程可進一步裝配成系統動力學方程。

1.2.3 彈性力的物理意義

由式(9)，單元彈性力Qs向量可寫為

(11)

式中:對于單元的節點i，fi為作用在節點i上的力;fix、fiy和fiz與施加在截面上的力矩有關。當施加在截面上的力矩為T=[TxTyTz]T時，有下式成立[14]

(12)

將式(12)直觀表達在單元上，如圖3所示。

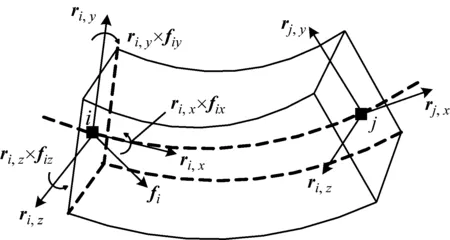
圖3 單元彈性力分量

圖4所示為柔順機構的建模求解過程，可以清晰地得到本文所介紹的兩種建模方法的應用流程。

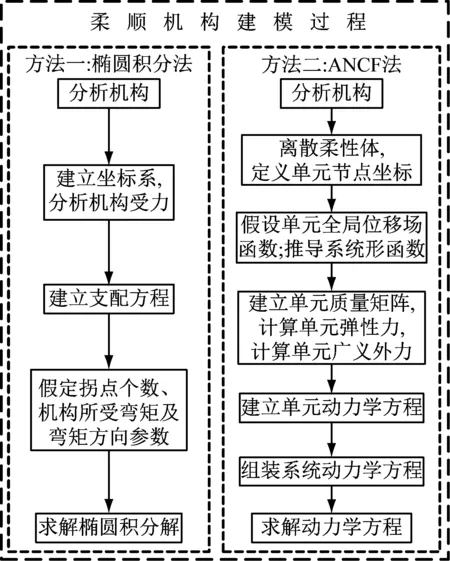
圖4 柔順機構建模過程

1.2.4 基于OpenMP并行編程

以上計算過程中，質量矩陣是常數矩陣，彈性力矩陣是時變的，且多次采用高斯-勒讓德積分，降低了計算效率。本文選用Intel visual fortran語言編制仿真程序，使用8核CPU的 DELL服務器硬件，在編制程序時采用基于OpenMP共享存儲并行編程的并行計算思路，使得計算效率極大提高。

2 柔順機構算例

2.1 固定-導向柔順梁

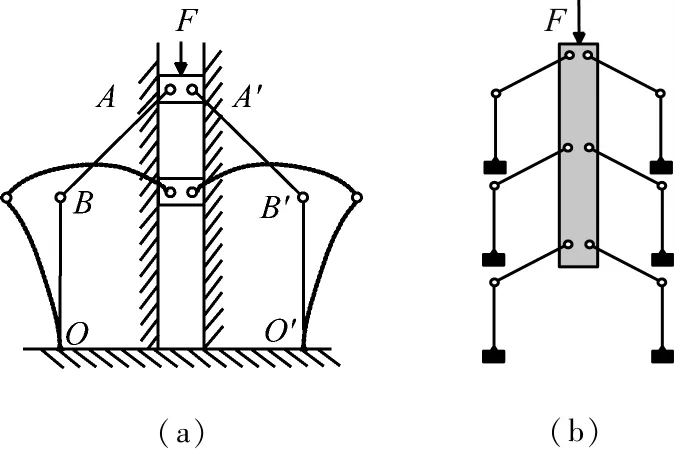
如圖5(a)所示的全柔順雙穩態機構兩側對稱，共包含4根柔順梁。為了簡化分析，取其中如圖5(b)所示的固定-導向柔順梁作為分析對象，圖中A端固定，另外一端B垂直向下運動，且B端截面轉角保持不變。梁AB初始傾角為β=30°，長度L=30 mm，矩形截面尺寸b×h=1×0.2 mm，彈性模量E=1.6×1011Pa，泊松比ν=0.3。設B端位移按式(13)函數規律加載。

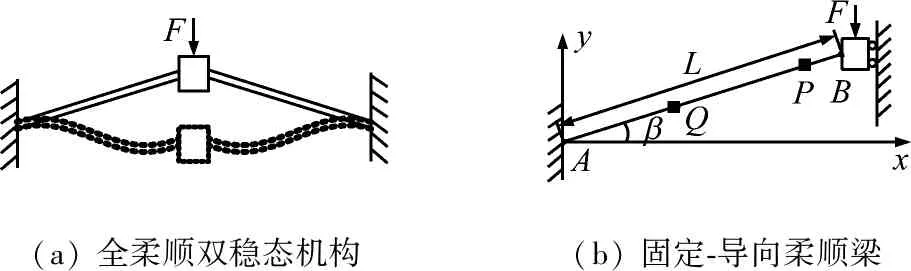
(a)全柔順雙穩態機構(b)固定-導向柔順梁

圖5 固定-導向柔順機構

Fig.5 Fix-guided compliant mechanism

(13)

式中:Vs為B端的最終速度，Ts為速度從0加載到Vs所用的時間，t為加載時間。

圖6所示為分別采用橢圓積分法和ANCF法計算固定-導向柔順梁運動時梁軸線的變形結果。從圖6中看出：兩種方法得到的變形基本吻合。梁AB從起始位置開始運動，并發生屈曲。初始階段，梁上有兩個拐點，隨著B端位移增大，靠近固定端A的拐點逐漸趨近A端直至消失，此后梁上只剩一個拐點。拐點數量的變化揭示了此結構兩種穩態的跳轉變化過程。需強調的是，在求解時，相較于橢圓積分法，ANCF法無須假設梁上拐點數目和末端彎矩方向。

采用ANCF法將柔順梁劃分為10個單元，如圖7所示為距梁B端3 mm處點P(如圖5(b))在x方向的位置隨時間變化曲線。圖中可以看出：正常加載時，0.03 s之后點P在x方向產生了劇烈的振動，這是因為0.03 s之前梁主要在軸向產生壓縮，在大約0.03 s時發生了屈曲，突然彎曲產生了劇烈的振動。在0.22 s時梁上兩個拐點變為一個拐點，梁的形態發生了跳轉。

應用ANCF法分析該柔順梁時，發現梁在屈曲的瞬間產生了較大的振動，而采用橢圓積分法則無法獲得該振動現象。為了驗證圖7中的結果，在如圖5(b)的Q點，梁屈曲前施加一個微小豎直向上的初始干擾，得到如圖7所示初始加干擾的P點x方向的位置變化曲線。可以看出，由于施加的初始干擾與梁屈曲變形方向一致，使得屈曲變形變得容易，則梁的振動明顯減小。當施加向下的干擾時，柔順梁軸線變形變成如圖8所示的另一種形態。

圖6 固定-導向柔順梁軸線變形

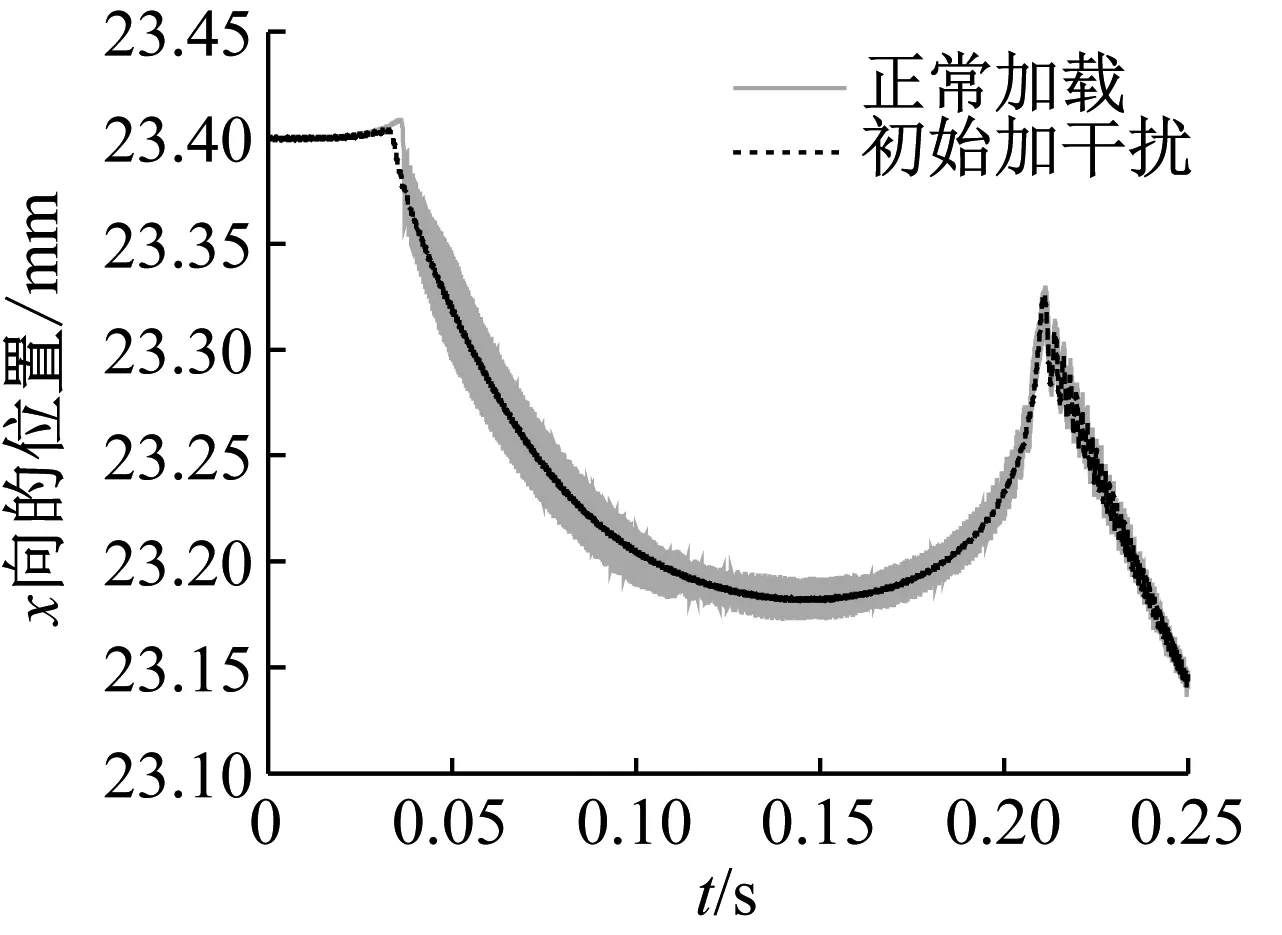
圖7 點P在x方向上的位置變化

為驗證圖6和圖8所示柔順梁仿真計算結果，設計了如圖9所示實驗裝置。圖9中采用XYZ平臺作為加載裝置，彈性梁3通過夾具分別與Z軸下端1、固定底板2固接。

(a)實驗臺(b)實驗臺實物

圖9 固定-導向梁變形實驗臺

Fig.9 Experiment facility of the fixed-guided beam

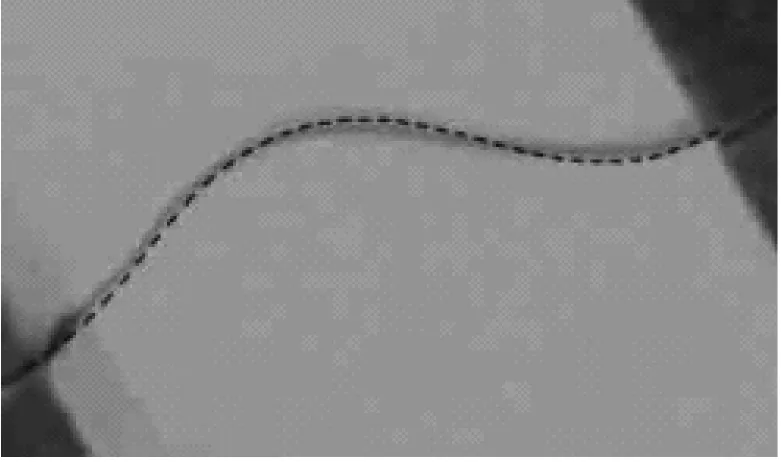
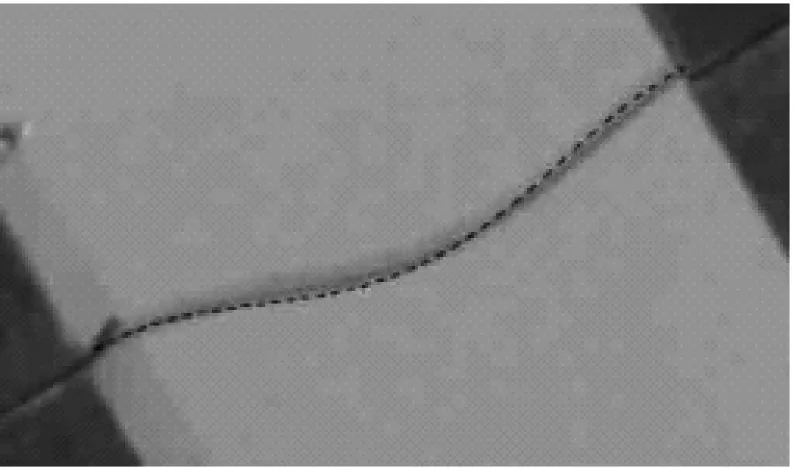
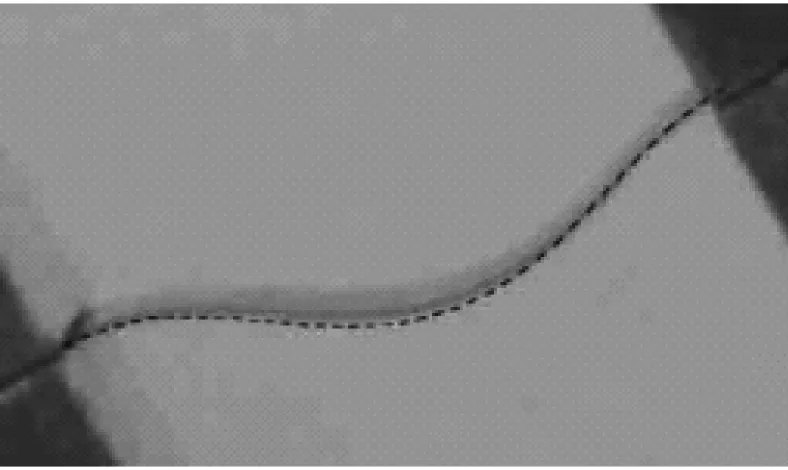
XYZ平臺的Z軸由控制器控制，按式(13)規律垂直運動，實現柔順梁一端運動、一端固定，同時自身發生變形。使用攝像機記錄施力過程中柔性梁的變形。ANCF法的數值仿真結果和實驗結果對比如圖10所示，其中虛線為數值結果，實線為實驗結果。可以看出理論和實驗結果基本完全吻合，驗證了理論計算結果的正確性。

根據式(12)，采用ANCF法求得圖5(b)中B端運動過程中的力F如圖11所示。圖中，力F同樣伴有劇烈震蕩；若施加初始向上/下的干擾時，振動減小，與橢圓積分法計算得到的力結果不吻合。在力F的作用下，B端從初始位置開始向下運動，在梁屈曲前發生軸向壓縮，力F迅速變大，當載荷大于屈曲臨界值時，梁發生屈曲；此后力F則隨位移的增大而減小，直至力F變為負值，梁發生了狀態的跳轉，拐點由兩個變為了一個。圖6和圖8所示的兩種變形形態得到的力F是相同的。需要指出的是：ANCF法中，梁屈曲前力F上升是由于梁發生了軸向壓縮，而橢圓積分法中梁屈曲前力F上升段沒有任何工程意義，只要給定足夠小的位移，并且能夠通過數值方法得到式(2)的解就能夠使梁屈曲時的最大力F無限接近y軸，與實際情況不符。

由于整個梁產生了大范圍的位移運動，因此為了方便觀察梁截面產生的剪切變形，將梁截面在梁單元的單元局部坐標系中繪出，如圖12給出了在梁AB上l=12 mm處梁截面的剪切變形情況。由圖12可以看出在梁的變形過程中，截面產生了顯著的剪切變形，截面尺寸拉伸和轉角變化明顯。

2.2 柔順雙穩態機構

為了進一步驗證ANCF法的有效性，對如圖13(a)所示柔順雙穩態復雜機構進行仿真。該機構包括一個滑塊、兩個柔性懸臂梁BO、B′O′和兩個鉸接-鉸接型柔性屈曲梁AB、A′B′，BO和B′O′對稱布置在滑塊兩側。該機構具有兩個穩態位置，滑塊對應處于頂端或底端。如圖13(b)，將相同拓撲特性的多組懸臂梁和鉸接-鉸接型屈曲梁串聯，可實現滑塊的精密微型直線運動。

圖13(a)中，桿OB和BA長度均為1.25 m，兩桿夾角為135°，截面為邊長0.03 m的正方形，彈性模量E=2.07×1010Pa。為求得使該機構越過平衡位置(即桿BA水平時)施加的最大外力，同樣在滑塊上按式(13)加載位移載荷，直到機構到達第二個穩態位置結束。由于結構是對稱的，只取其左半部分進行分析。圖14所示給出了機構從第一個穩態位置開始運動到第二個穩態位置的變形過程。圖15給出了機構運動過程中，施加的外力的變化規律。從圖14、15可以看出，當t=1 s時，桿BA到達水平位置，施加的豎直力F變為0，當t=1.8 s時機構達到第二個平衡位置，施加的力F再次變為0。軌道對滑塊的水平約束力如圖16所示，可以看到水平約束力最大位置在桿BA越過平衡位置之后出現，并不是在桿BA水平時水平約束力最大。由變形可以進一步計算出O處的彎矩，如圖17所示，其量值決定了機構的壽命。

t=0.06 s

t=0.08 s

t=0.10 s

t=0.12 s

t=0.14 s

t=0.16 s

t=0.18 s

t=0.20 s

(a) 與圖6對應的變形(虛線為仿真結果，實線為實驗結果)

t=0.06 s

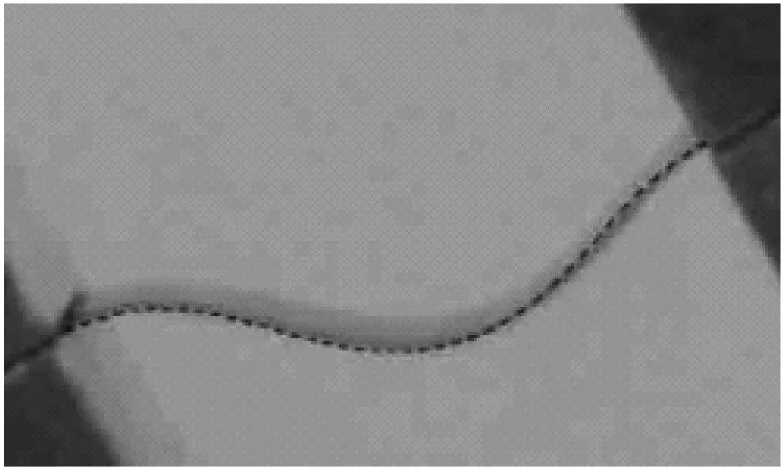
t=0.08 s

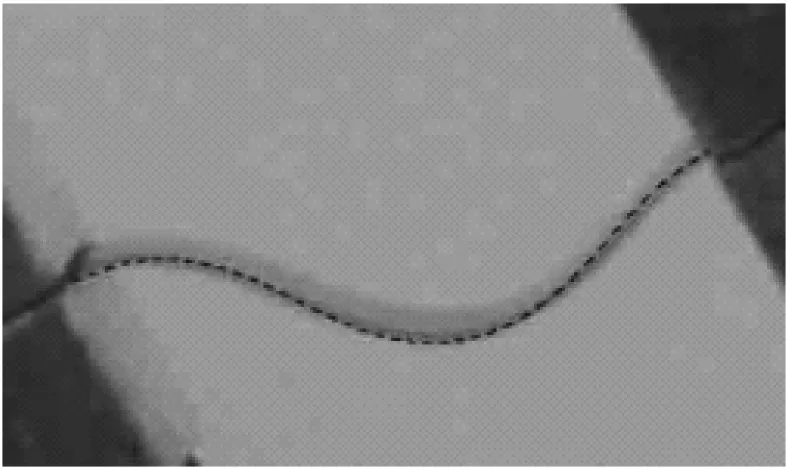
t=0.10 s

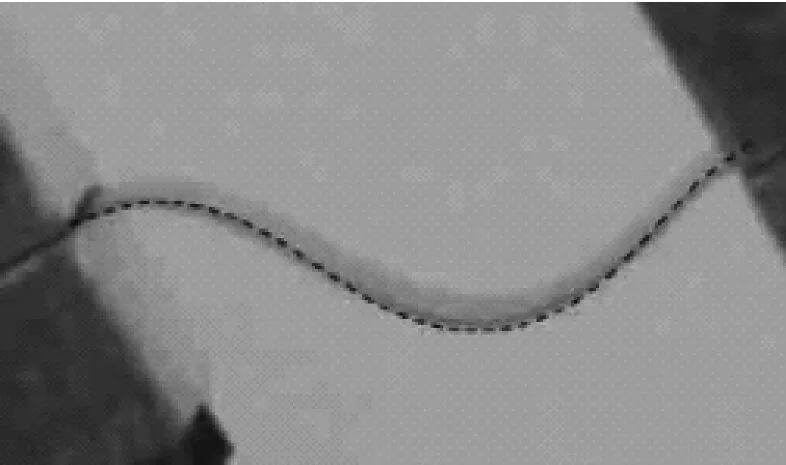
t=0.12 s

t=0.14 s

t=0.18 s

t=0.20 s

t=0.22 s

(b) 與圖8對應的變形(虛線為仿真結果，實線為實驗結果)

圖10 實驗結果與仿真結果比較

Fig.10 Deformation comparison of the experimental results with that of the simulation

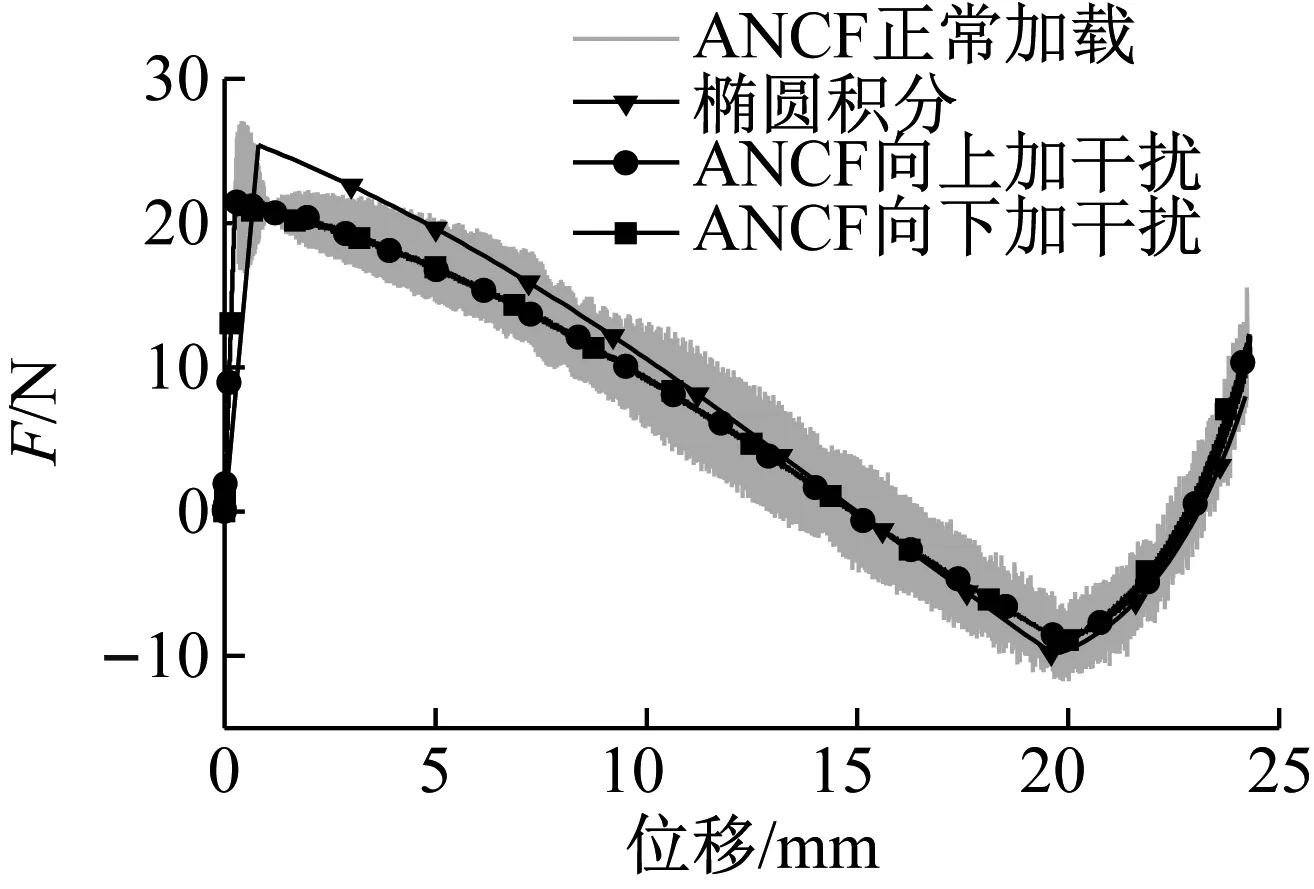
圖11 力F和末端B位移的關系

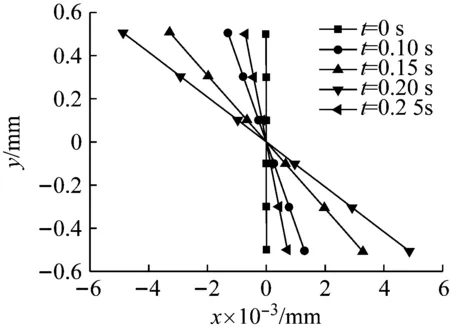
圖12 梁上l=12 mm處截面的剪切變形

(a)(b)

圖13 柔順雙穩態機構

Fig.13 Compliant bistable mechanism

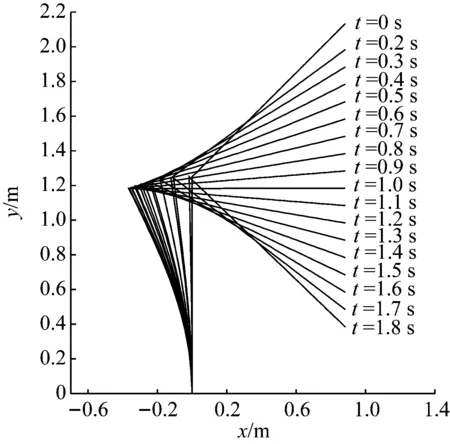
圖14 柔順雙穩態機構的變形過程

經過以上兩個算例的分析和比較，可以看到橢圓積分法基于歐拉伯努利梁理論，忽略了梁截面的剪切和軸向變形，在解支配方程時需要預先假定拐點的個數和梁末端的彎矩方向，對位置數的求解順序也有一定的要求，計算用時少，但不確定性增加。而ANCF法可以計及梁的軸向變形、彎曲變形和截面的剪切變形，能更精確地描述大變形大位移大轉動問題，通用性強，非常適合于柔順機構建模與其動力學特性分析，采用多線程并行算法可以提高計算效率。

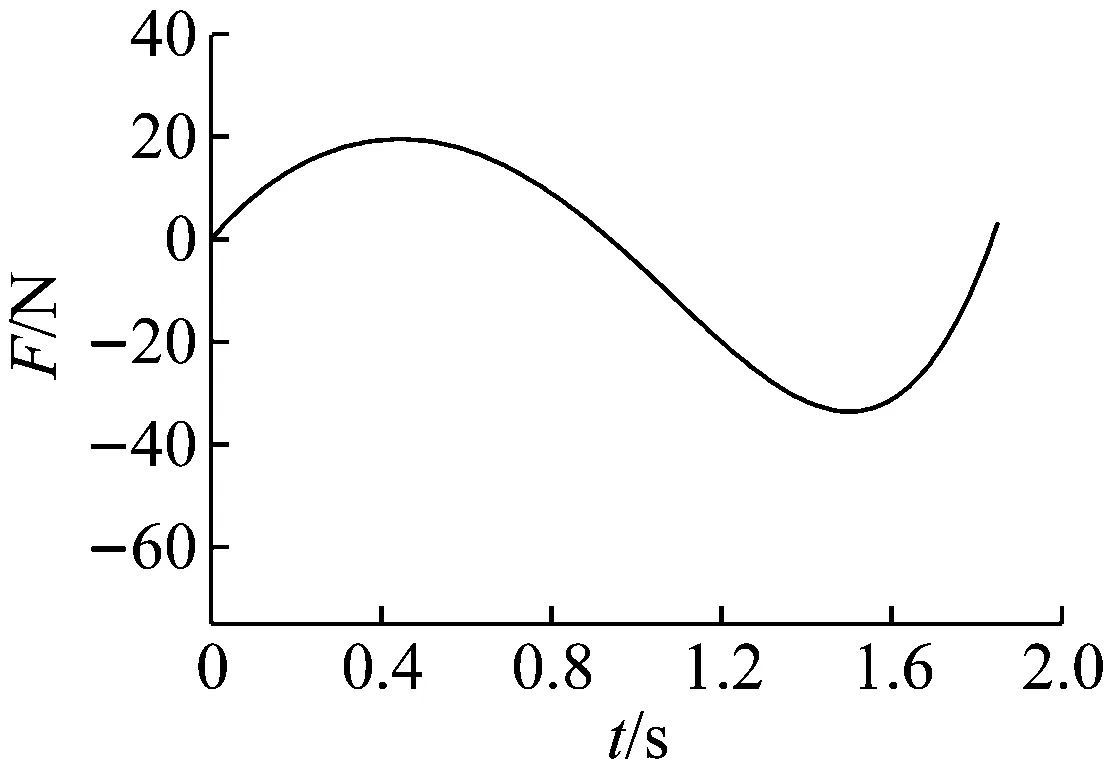
圖15 豎直力F隨時間t的變化規律

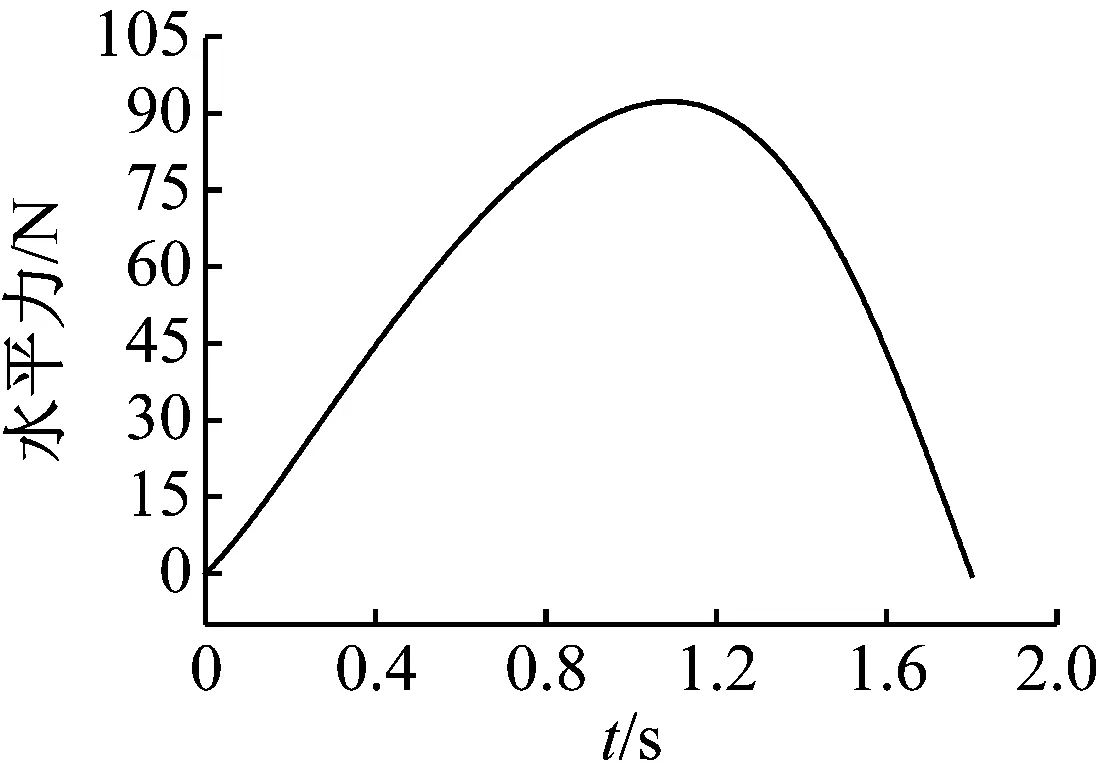
圖16 水平力隨時間t的變化規律

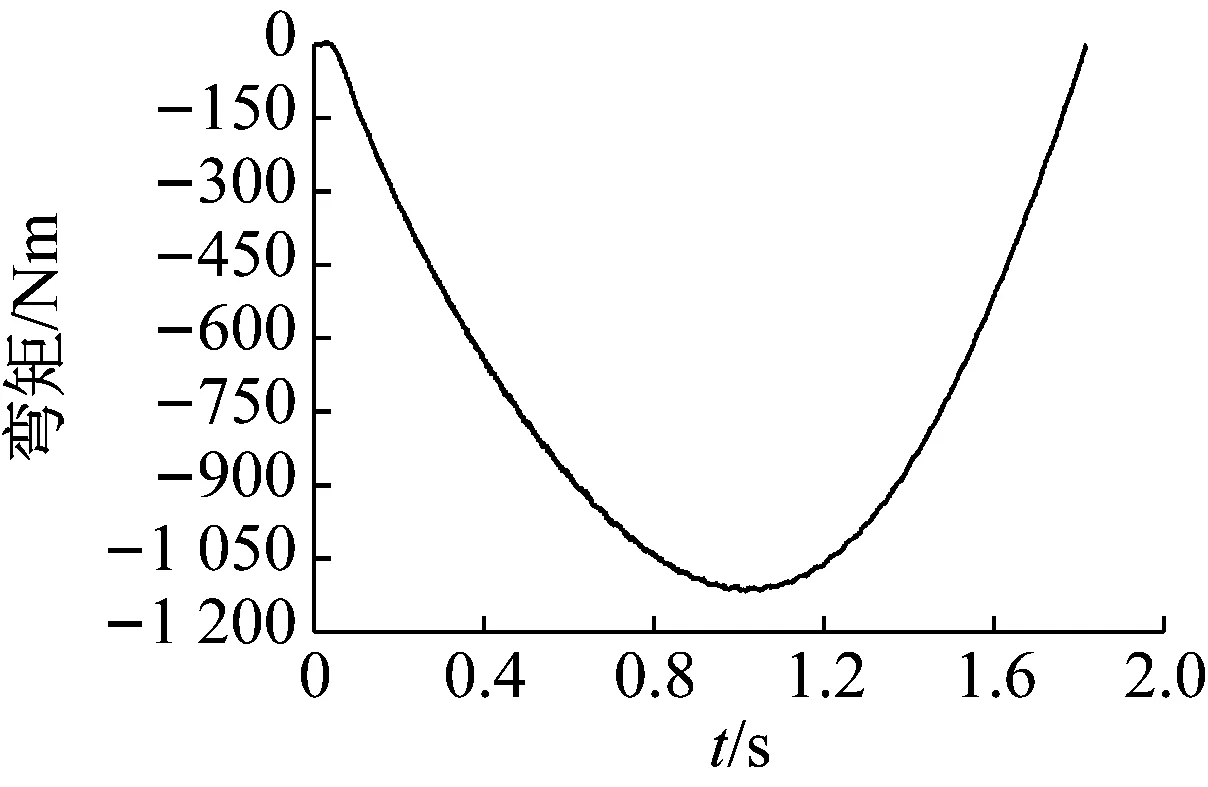
圖17 點O處彎矩隨時間t的變化規律

Fig.17 The relationship between the bending moment ofOand time

3 結 論

柔順機構由于含非線性變形大運動構件，其建模變得困難。本文首先簡述了基于Euler-Bernoulli梁理論的橢圓積分法和基于Timoshenko梁理論的絕對節點坐標法的基本原理，以固定—導向柔順梁為例，仿真與實驗結果證明了兩種方法對簡單柔順機構建模與分析的有效性；其次采用ANCF法對柔順雙穩態機構進行建模與分析，驗證了ANCF法對復雜柔順機構動力學特性分析的有效性。通過對比兩種方法的原理和仿真便利性，顯示ANCF法對柔順機構建模與分析更具有優越性，為柔順機構這類現代機構學產品的工程設計與分析，提供了一種精確而高效的方法。