基于線調頻小波路徑追蹤和逐步解調濾波的滾動軸承故障診斷
劉東東, 程衛東, 溫偉剛
(北京交通大學 機械與電子控制工程學院, 北京 100044)
滾動軸承是旋轉機械最關鍵的部件之一,由于其常處于變載荷﹑變轉速的工況中,工作環境惡劣,極易發生故障[1-2]。階比跟蹤技術是最常用的處理時變工況下振動信號的方法[3]。階比分析中鑒相時標的確定需要轉速信息,轉速可以通過轉速計測取,也可以在信號中提取[4]。由于測取轉速受到安裝成本以及安裝空間的限制,如何提取轉速引起學者的研究。文獻[5]提出了基于多尺度線調頻基的稀疏信號分解方法,自適應地選取適當尺度對振動信號投影分解,提取齒輪包絡信號的瞬時頻率。但是處理滾動軸承振動信號時,高幅值的故障特征頻率(Fault Characteristic Frequency, FCF)會干擾轉頻的提取。文獻[6]使用FCF代替轉頻對信號重采樣,根據故障特征階比模板判斷軸承故障。文獻[7]根據估計轉頻的范圍構造一組帶通濾波器對特征頻率進行濾波,根據依靠等效轉頻采樣得到的故障相角域判斷軸承狀態。雖然根據等效轉頻進行階比分析可以恢復信號的周期性,但是等角度重采樣過程復雜,計算效率較低[8]。文獻[9]也證明階比分析存在包絡畸變現象。
廣義解調時頻分析算法[10]可以將時頻分布為傾斜、非線性的頻率分量轉換成平行于時間軸的頻率。由于其非常適用于處理非穩態的調幅-調頻信號,已經開始應用于振動信號的處理。文獻[11]使用廣義解調時頻分析,將齒輪振動信號分解為若干個單分量信號,再對各個單分量信號進行包絡分析,得到包絡階次譜。文獻[12]通過對齒輪振動信號進行基于多尺度線調頻基的稀疏信號分解,估計嚙合頻率,再對信號進行廣義解調和FFT變換,得到齒輪的FCF。然而,在軸承的振動信號中,由于調制轉頻分量太小,因此很難直接提取,用于估計相位函數。文獻[13]將廣義解調算法應用到滾動軸承的故障診斷中,但是相位函數的估計以實測轉速為基礎,在實際工況中,會受到安裝成本以及安裝位置的制約,此算法的應用也會受到限制。
從以上分析可知,以階比分析為基礎的軸承故障診斷法會有效率以及誤差等問題,而廣義解調算法的使用會依賴轉速計等輔助設備。當工況變化時,軸承故障引起的高頻共振不僅會調制FCF,而且FCF也會調制轉頻。因此,理論上在包絡時頻譜(Time-Frequency Representation, TFR)中會有轉頻分量,但是,轉頻的幅值一般較小,很難直接提取[14]。瞬時故障特征頻率(Instantaneous Fault Characteristic Frequency, IFCF)具有幅值優勢[15],一般容易提取。文獻[16]提出了線調頻小波路徑追蹤(Chirplet Path Pursuit, CPP)算法,該算法與常用提取頻率的峰值搜索算法相比,抗噪聲能力強,擬合精度較高。文獻[17]使用CPP算法估計齒輪嚙合倍頻和軸承IFCF,判斷含有齒輪振動下的軸承運行狀態。文獻[18]根據CPP算法估計的IFCF和轉頻對應關系,判斷軸承故障位置,但是該算法以實測轉速為參考。
本文利用CPP算法的優良特性,使用該算法在降采樣的包絡信號中估計IFCF趨勢線,據此計算IFCF的相位函數。然而,僅僅依靠IFCF在解調頻譜中的峰值,無法判斷故障位置,甚至出現誤判。為此,本文利用估計的IFCF,根據軸承各部分故障特征因子,采用重復估計轉頻的方式,計算潛在的轉頻。根據IFCF和轉頻的相位函數,構造逐步解調濾波算法,對信號各頻率進行逐步解調和濾波。通過對仿真信號和試驗信號的處理,證明了該算法的有效性。
1 算法部分
為了在不使用轉速測量設備的情況下,對軸承故障位置進行辨別,應對軸承信號的特點進行分析,以提取必要瞬時頻率,估計相位函數。若滾動軸承出現局部故障,故障點與配合面會形成一系列沖擊,該沖擊會激起系統的高頻共振。轉速不變時,沖擊間隔相等,間隔的倒數就是故障特征頻率[19]。理論上FCF只與轉速、故障位置和軸承參數相關,外圈、內圈和滾珠存在故障時的故障特征頻率fo,fi和fb的公式
(1)
(2)
(3)
式中:fr為轉速,N為滾動體個數,D為節圓直徑,d為滾動體直徑,φ為接觸角。
1.1 線調頻小波路徑追蹤
CPP算法是近年提出的一種檢測瞬時頻率的算法, 它的原理是將信號劃分為一系列的動態時間支撐區,從建立的Chirplet原子庫中,按照相關性最大的原理,選擇各支撐區間的原子,根據最佳路徑連接原則對選定原子進行連接,依據各個支撐區間的原子的頻率估計信號的瞬時頻率。
建立Chirplet原子庫
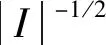
(4)
式中:I為動態時間支撐區間,I=[kN2-j,(k+1)N2-j]×Δt;k為區間的序號,k=0,1,…,2j-1;N為采樣長度;j為區間尺度系數,j=0,1,…,log2N-5;1I(t)為矩形窗函數,即t∈I時,1I(t)=1;t?I時,1I(t)=0;aμ為線調頻小波的調頻率系數;bμ為頻率的偏置系數;按照采樣定理,aμt+bμ應小于fs/2.
定義信號的chirplet變換為信號與原子庫中所有原子的內積
(5)
式中:t=n×Δt,n為t時刻點數,Δt為采樣時間間隔。
在原子庫中挑選一組原子進行連接,使分析信號y(t)在時間支撐區I上的具有最大投影系數
(6)
設時間支撐區I內的最大投影系數kI表示的信號分量為dI(t)
dI(t)=|kI|exp[-i(at2/2+bt)]1I(t)
(7)
連接投影系數kI表示的信號分量dI(t),使得信號d具有最大的總能量
(8)
式中:Π包含信號的整個時間長度,而且不重疊。
該算法的具體連接方法如下:
(1) 初始化,設置e(i)=0,pred(i)=0,其中,e(i)為選擇的i-1個動態時間支撐區的信號的總能量,pred(i)為第i個時間支撐區的前置支撐區的序號。
(2) 對動態時間支撐區集合{Ii|i∈z},尋找相鄰的下一個動態支撐區的集合{Ik|k∈z},如果e(i)+d(i)>e(k),則有
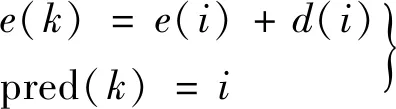
(9)
該連接算法能保證Chirplet原子的組合與原信號的相似度最高。因此,CPP算法是通過連接各個支撐區的瞬時頻率為線性的原子逼近信號的瞬時頻率。
1.2 廣義解調算法
由于轉速的變化使軸承故障引起的沖擊失去了周期性,信號的頻譜出現頻率模糊現象,因此,有必要將時變頻率轉化為周期頻率。廣義解調算法是一種新的處理時變信號的方法,可以根據相位函數將非周期的瞬時頻率轉換為周期頻率。該算法的本質為廣義傅里葉變換,對于信號x(t),其廣義傅里葉變換的定義為
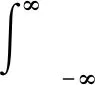
(10)
式中:s0(t)為與時間t相關的實值函數,這實際是對x(t)e-2πjs0(t)做標準的傅里葉變換。
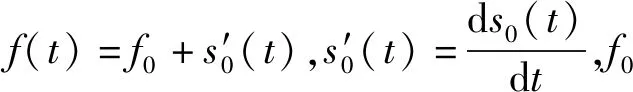
2 軸承的故障診斷方法
對于某一特定時變頻率,廣義解調算法可以根據該頻率的相位函數將其轉變為周期頻率。因此,在頻譜中該頻率由模糊轉化為突出的峰值。利用CPP算法可以在包絡信號中估計IFCF,因此,根據估計的IFCF可以實現對其解調。但是僅僅依靠該峰值,無法判斷軸承故障及其位置。這是因為轉子失衡或者安裝原因也會產生隨轉速變化的頻率,如果利用CPP算法估計的瞬時頻率為該頻率,對其解調也會出現峰值。因此,如果判斷該頻率是軸承故障引起的,還要辨別故障位置,必須需要借助參考頻率。
在變轉速的工況下,高頻共振不僅會調制FCF,而且FCF還會調制轉頻。由于轉頻的幅值較低,一般很難在信號中直接估計。假設估計的IFCF是外圈故障引起的,根據FCF與轉頻的比例fr=fcf/Co(Co為外圈故障特征系數),可以計算潛在轉頻。如果在解調濾波后的轉頻位置不出現峰值,那么該故障就不是外圈故障,然后再假設內圈故障,對轉頻進行估計。為了減少FCF以及幅值較小的轉頻被噪聲污染,可以對解調后的信號進行帶通濾波,濾除背景噪聲和解調造成的頻率干擾。這里將根據CPP算法估計的軸承IFCF,依據特征系數計算其他頻率,根據得到的頻率對信號進行逐步解調,恢復各頻率的周期性,然后通過帶通濾波濾除噪聲,這種處理方式稱為逐步解調濾波算法。該算法主要包括:① 使用CPP算法估計IFCF;② 利用估計的IFCF計算諧頻及轉頻;③ 根據各頻率估計相位函數;④ 根據相位函數對信號進行解調;⑤ 對解調信號逐步帶通濾波。
為了直觀描述算法原理,圖1給出了一個仿真信號的處理實例。假設f(t)為IFCF,fr(t)為轉頻,通過提取的IFCF趨勢線可以估計IFCF的相位函數,假設外圈故障,便可以通過式(1)計算轉頻,進而估計出轉頻的相位函數。使用帶通濾波器對解調后信號進行濾波,然后對濾波信號求和,便可以求得IFCF和轉頻解調濾波信號。如果假設正確,在頻譜的fo和fr的位置會出現峰值。

(a) 原始信號時頻譜

(b) 解調信號的時頻譜

(c) 解調信號f′(t)的時頻譜

(d) 解調濾波信號的時頻譜

(e) 解調濾波信號f′(t)的時頻譜

(f) 逐步解調濾波信號時頻譜
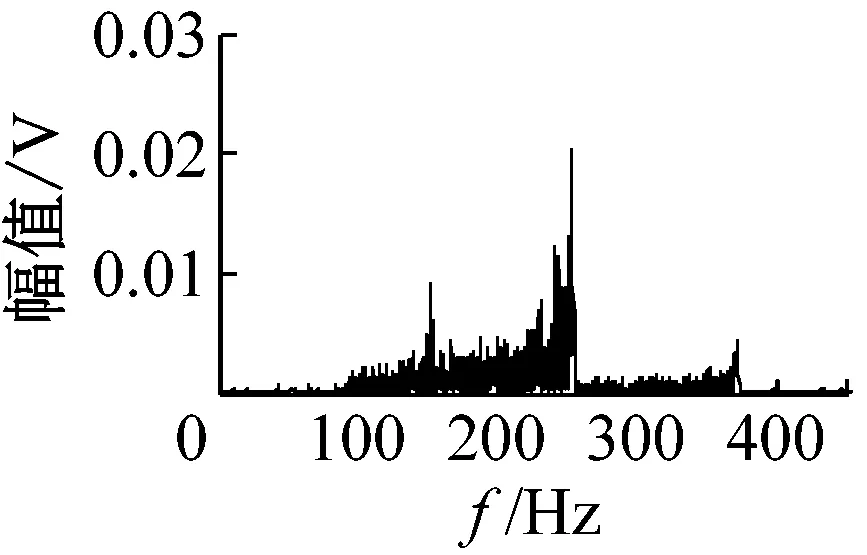
(g) 原始信號的頻譜
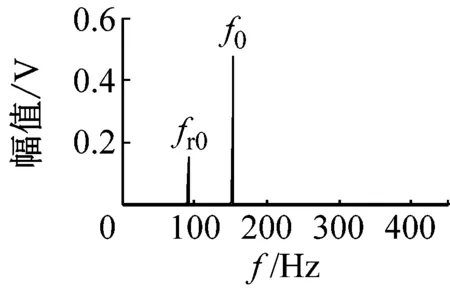
(h) 逐步解調濾波信號的頻譜
圖1 逐步解調濾波算法流程圖
Fig.1 Flowchart of stepwise demodulation filter algorithm
基于CPP和逐步解調濾波的滾動軸承故障診斷方法的具體步驟如下:
步驟1根據軸承的幾何參數,結合式(1)~式(3),計算軸承各個部分的故障特征系數Co=fo/fr,Ci=fi/fr,Cb=fb/fr。
其中,Co,Ci和Cb分別表示外圈、內圈和滾動體的故障特征系數。
步驟2對原始信號進行Hilbert變換得到包絡信號,使用CPP算法在降采樣包絡信號中估計IFCF,并使用多項式對其進行擬合f1(t),計算IFCF的倍頻
(11)
其中,f1(t)為IFCF的擬合方程,an,…,a1,a0均為常數。
步驟3假設外圈、內圈和滾動體出現故障,并估計對應轉頻fro1(t)=f1(t)/Co,fri1(t)=f1(t)/Ci和frb1(t)=f1(t)/Cb以及倍頻。
其中,fro1(t),fri1(t)和frb1(t)分別表示外圈、內圈和滾動體出現故障時的轉頻。
步驟4構造解調函濾波的相位函數
(12)
并求得解析信號y(t)=x(t)+jH[x(t)],其中H[x(t)]是x(t)的Hilbert變換,對y(t)進行廣義解調后得到解析濾波分量dk(t)=yk(t)e-2πjsk(t)。其中:fk(t)為f1(t)及其倍頻;fro1(t),fri1(t)和frb1(t)及其倍頻;fk(0)為對應頻率的初始值。
步驟5以擬合函數fk(t)的初始值fk(0)為中心頻率,fwidth為帶寬,構造窄帶帶通濾波器。使用該濾波器對解調后的信號濾波,得到解調濾波信號mfk(t)。對濾波后的解調信號mfk(t)求和便可以得到逐步解調濾波的信號
mf(t)=∑mfk(t)
(13)
步驟6對逐步解調濾波信號mf(t)進行FFT變換得到解調濾波信號的頻譜,根據頻譜完成故障診斷。
3 仿真分析
為了驗證算法的有效性,構造了變轉速軸承仿真模型x(t)并對其進行分析。仿真模型x(t)由軸承故障引起沖擊x1(t)和高斯噪聲n(t)構成
x(t)=x1(t)+n(t)
(14)
故障軸承的沖擊成分x1(t)的表達式
(15)
式中:N為沖擊數量,Am為第m個沖擊的幅值,由于軸承轉速越大,沖擊幅值越大,設置Am隨著轉速線性增加,β為結構衰減系數,u(t)為單位階躍函數,wr為軸承故障激發的系統的共振頻率,tm表示第m個沖擊出現的時間,tm由遞推公式(16)確定
(16)
式中:f(t)為滾動軸承轉頻;τ為滾動體的滑移引起的沖擊間隔誤差,一般為0.01~0.02;n代表軸承轉動一周產生的沖擊數。
設置軸承轉速變化規律為f(t)=10t+5(r/s),設置外圈和內圈故障特征因子為Co=3.5和Ci=5,其他參數如表1所示。

表1 仿真信號參數表
處理軸承外圈發生故障的仿真數據,截取3~6 s的數據進行分析。根據設置轉速f(t)=10t+5(r/s),該時間段內轉速線性增加,變換范圍為35~65 Hz。
圖2為仿真信號的時域波形圖,觀察可知,隨著轉速升高,波形幅值變大。圖3為仿真信號頻譜。使用CPP算法在降采樣的包絡信號中估計,如圖4所示的IFCF趨勢線。按照逐步解調濾波算法的步驟,對信號進行處理,得到如圖5所示的頻譜。根據相位函數的構造方式,如果是外圈故障,解調頻譜理論出現峰值的位置應該為轉頻的初始值35 Hz,外圈FCF的初始值35×Co=122.5 Hz及其倍數處。如果是內圈故障,則在轉頻,內圈FCF的初始值35×5=175 Hz及其倍數
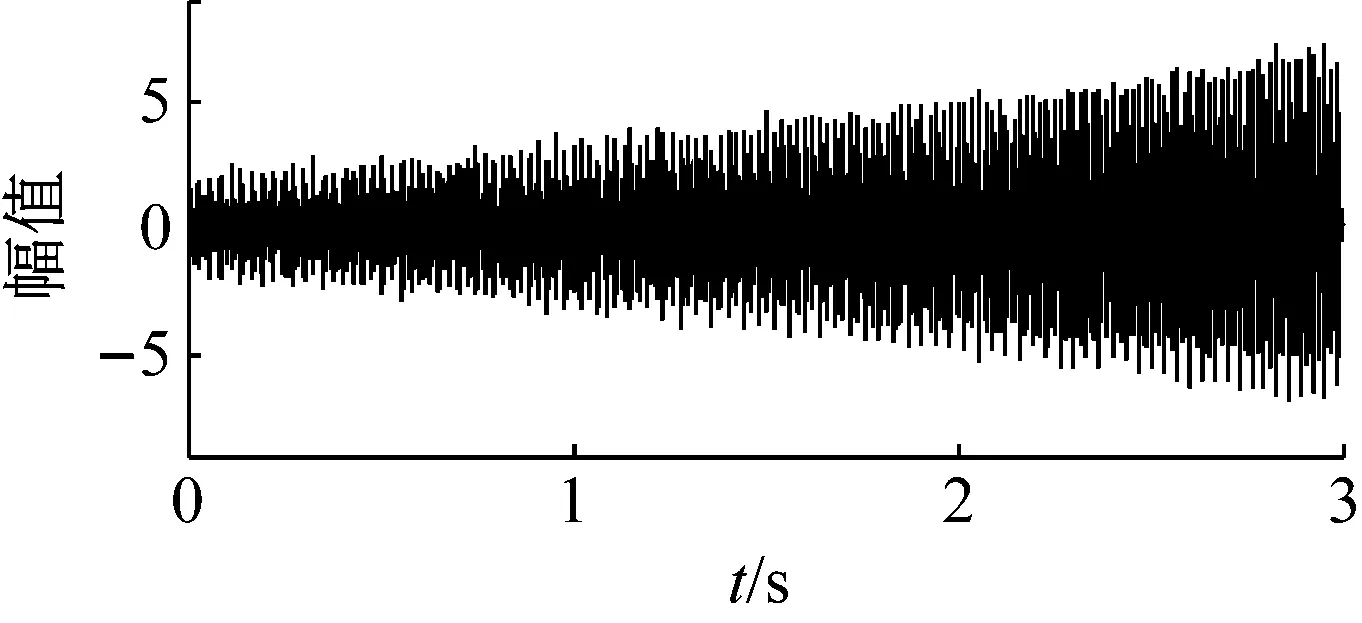
圖2 仿真信號的時域波形圖
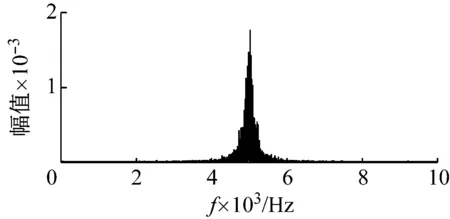
圖3 仿真信號的頻譜
出現峰值。 觀察解調頻譜,出現峰值位置符合理論計算的外圈出現故障的位置,由此可判斷軸承外圈出現故障。在如圖6所示的包絡頻譜中無突出的峰值,證明了該算法的可以提高頻譜質量。

圖4 提取的IFCF趨勢線
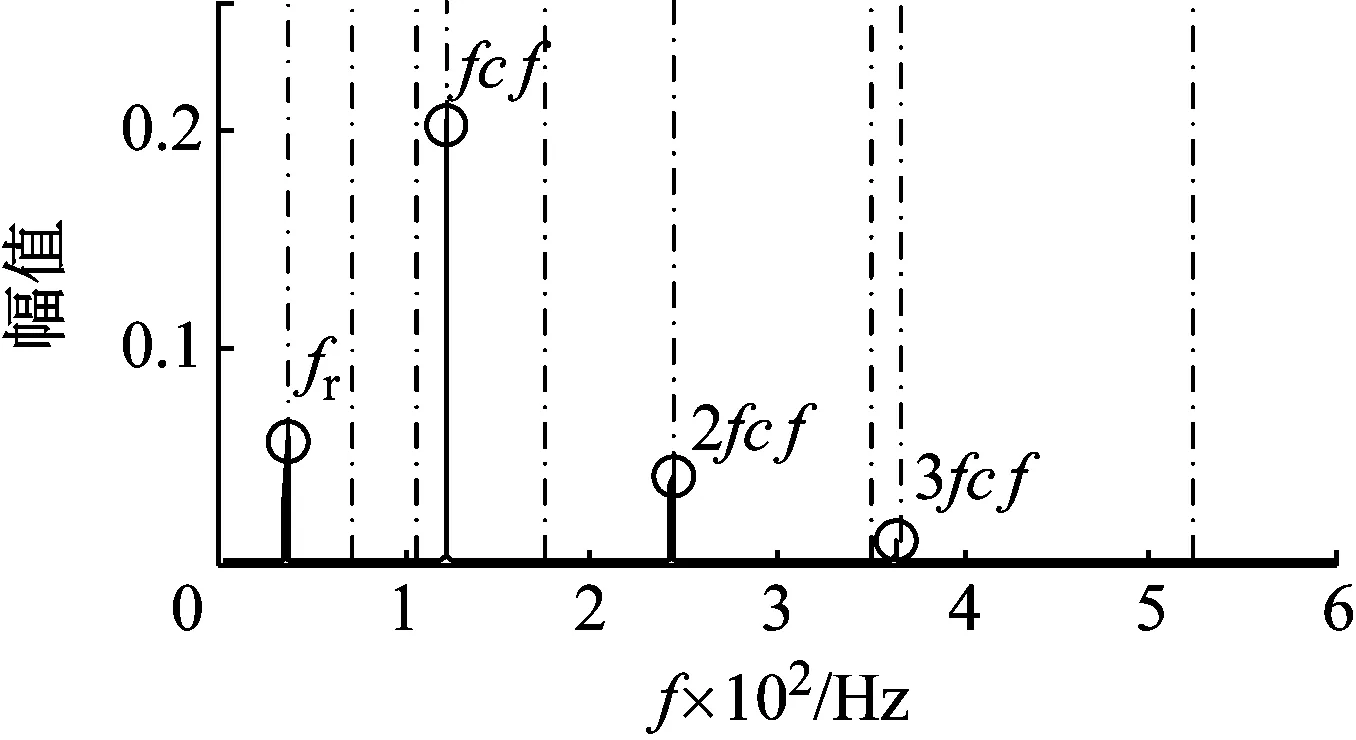
圖5 逐步解調濾波信號的頻譜
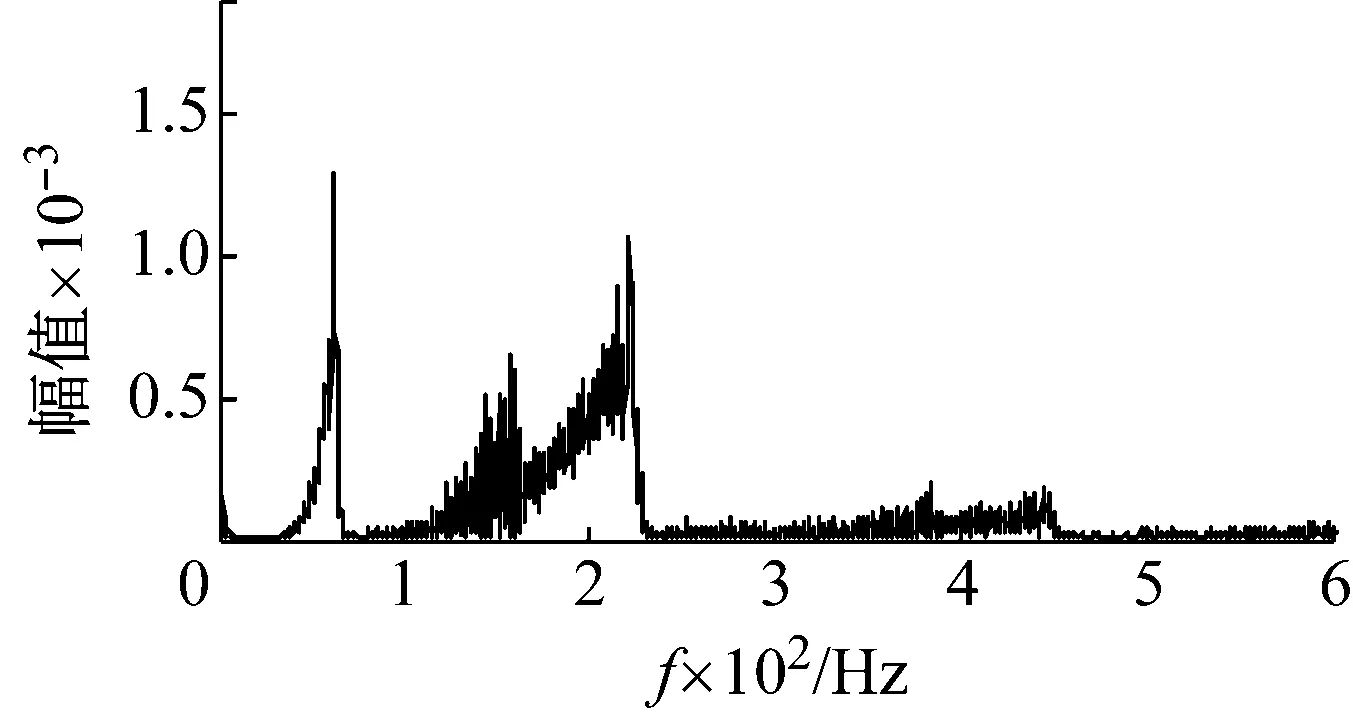
圖6 原始信號的包絡頻譜
4 試驗驗證
利用振動試驗臺測取變轉速工況下的振動信號,通過處理試驗信號,對算法的有效性進一步驗證。其中,為了模擬軸承故障,使用電火花對軸承的外圈和內圈加工裂紋,試驗使用軸承如圖8所示。試驗臺的結構如圖7所示。軸承的參數見表2。

圖7 試驗臺的結構
根據試驗滾動軸承的具體參數得到試驗軸承的外圈、內圈以及滾動體的故障特征系數分別為Co=2.55,Ci=4.45和Cb=1.7。

圖8 試驗滾動軸承

軸承型號滾珠數n滾珠直徑d/mm節圓直徑D/mm接觸角α600074.817.650
對升速狀態下外圈故障滾動軸承信號進行處理,圖9為振動信號的時域波形圖。圖10為根據轉速計測得脈沖擬合的轉頻。使用CPP算法在如圖11所示的降采樣的包絡信號中,估計IFCF趨勢線如圖12所示。利用多項式擬合IFCF趨勢線,并按照逐步解調濾波算法的步驟處理包絡信號,得到逐步解調濾波信號。對逐步解調濾波信號進行FFT變換,得到了如圖13所示的頻譜圖。觀察可知,峰值位置符合試驗軸承的外圈故障出現故障時的計算值,因此外圈存在故障。原始包絡信號的頻譜如圖14所示。圖14無突出峰值,通過對比證明該算法的有效性。
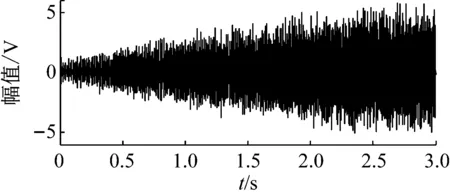
圖9 試驗信號的波形圖
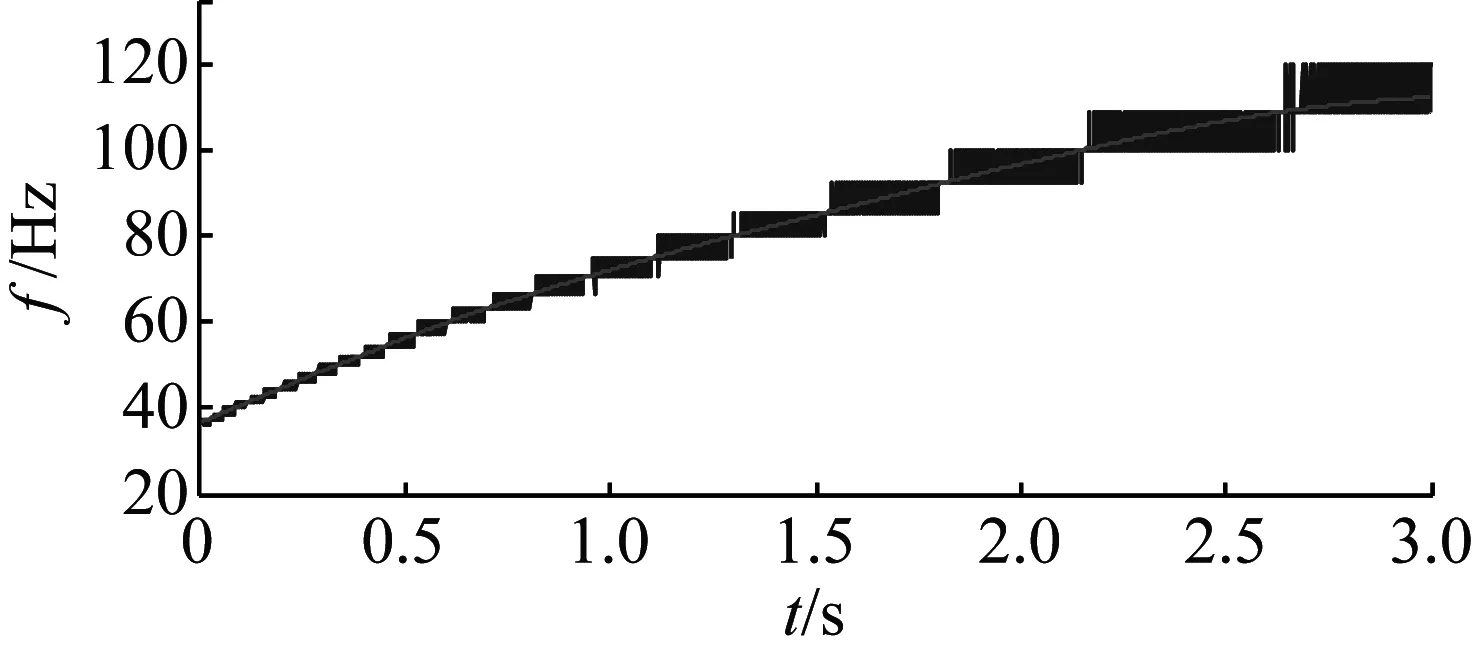
圖10 試驗測得轉速

圖11 包絡信號
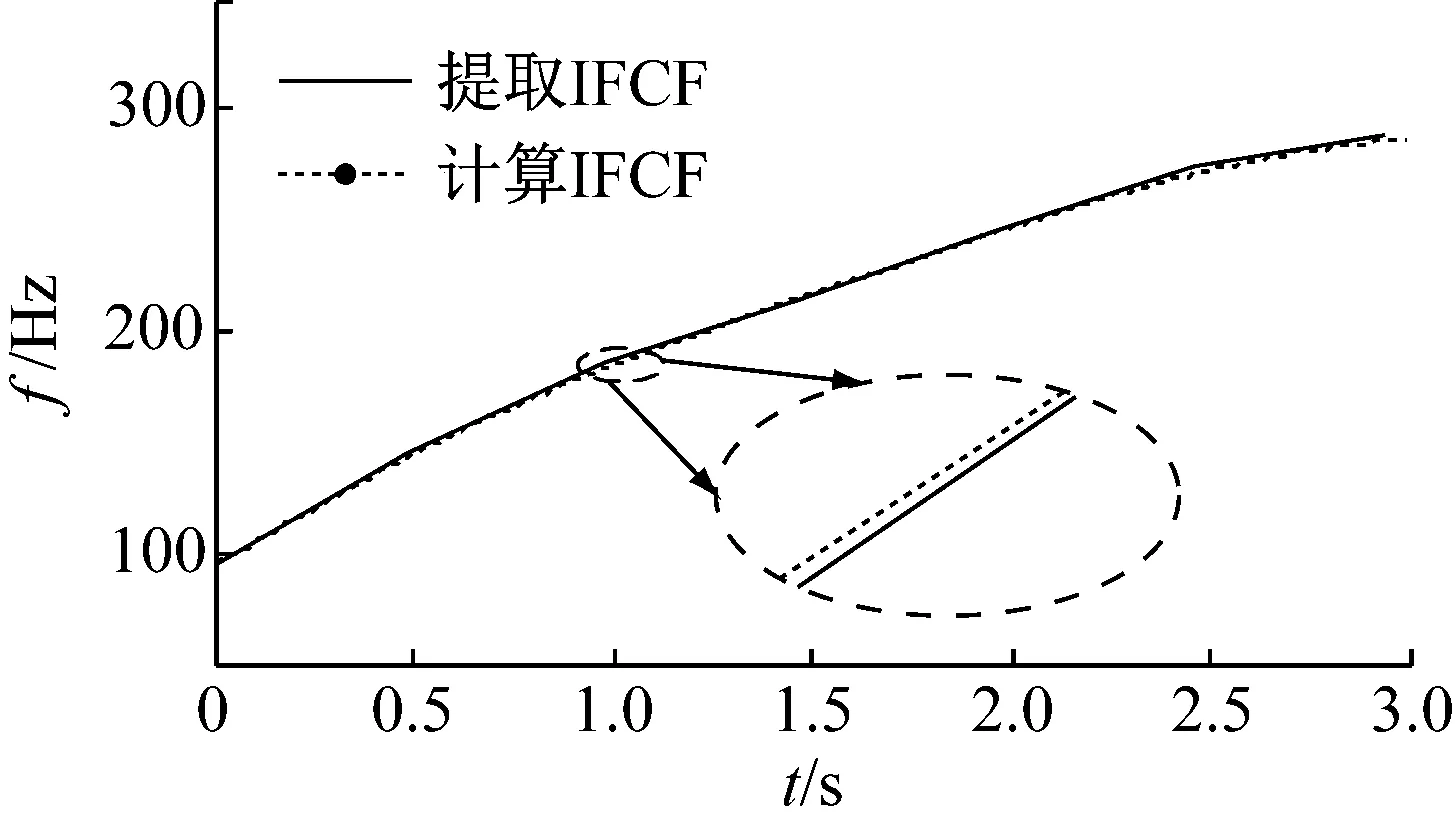
圖12 提取的IFCF趨勢線
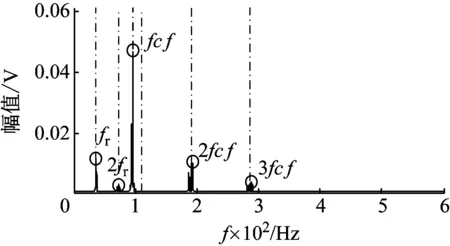
圖13 逐步解調信號頻譜
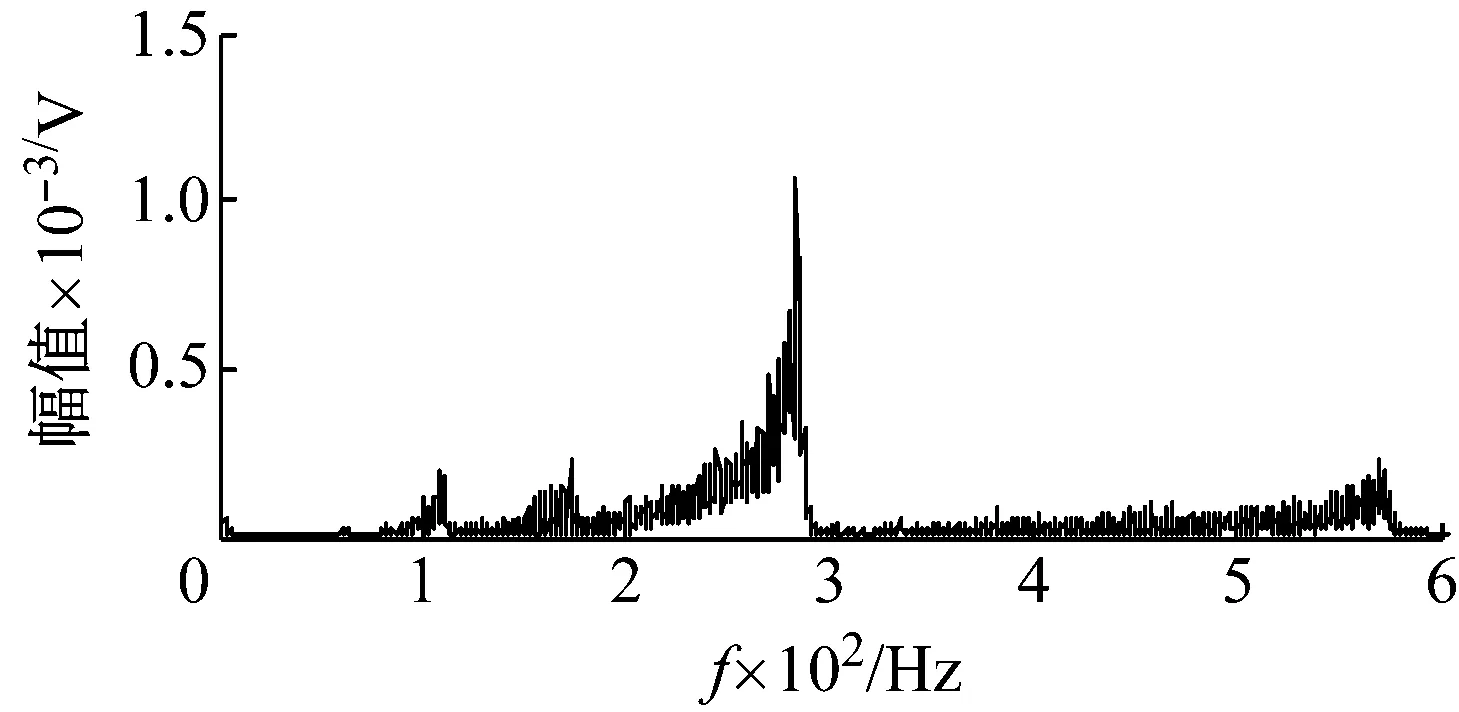
圖14 包絡頻譜
為了進一步驗證提出算法的有效性,對降速狀態下內圈故障滾動軸承信號進行分析。時域波形如圖15所示。圖16為逐步解調濾波頻譜圖。觀察可知,頻譜峰值位置與試驗軸承內圈出現故障計算值吻合,由此便可判斷軸承內圈出現故障。通過試驗信號的處理證明了提出算法的有效性。
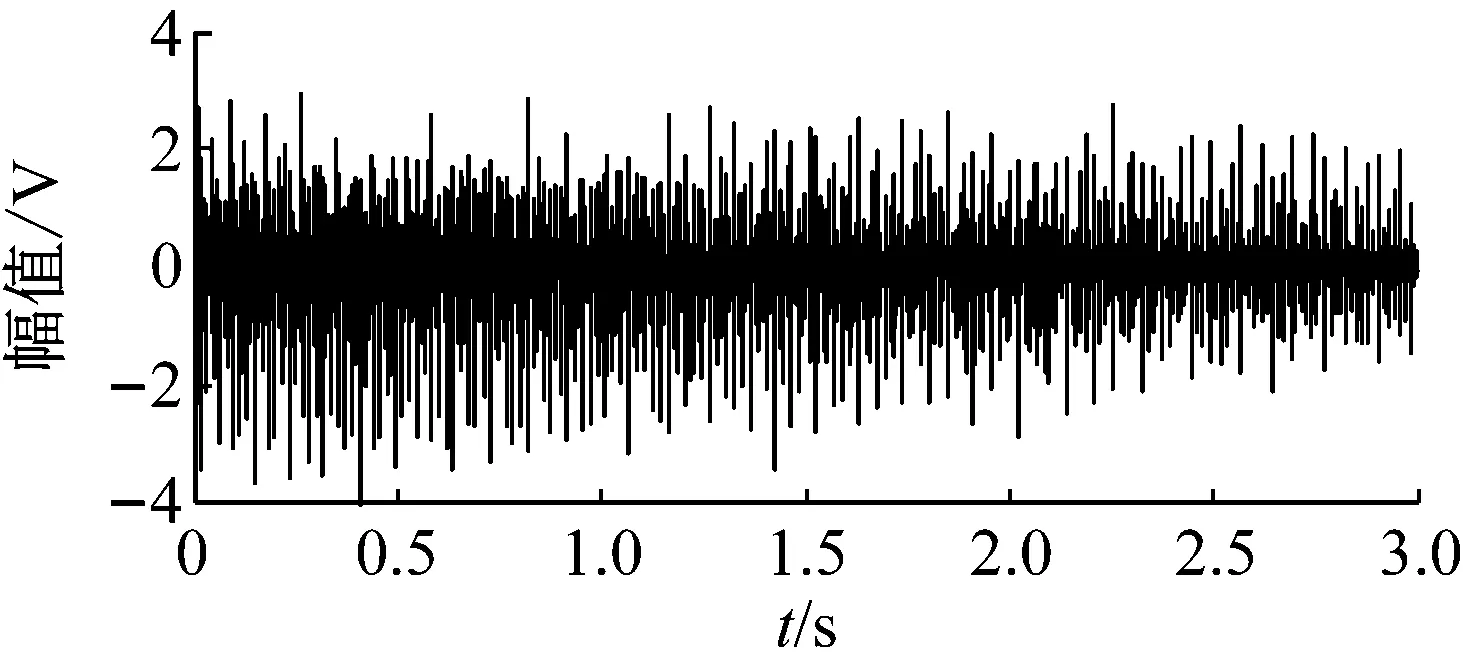
圖15 試驗信號的波形圖
5 結論
(1) 針對變轉速工況下,共振頻帶不僅會調制FCF,而且FCF也會調制轉頻這一現象,根據軸承不同位置的故障特征系數不同,以FCF為基礎,轉頻為參考的方式判斷軸承故障位置。
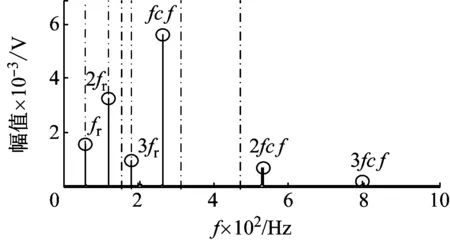
圖16 逐步解調濾波信號的頻譜
(2) 針對變轉速工況下滾動軸承振動信號中缺少易于提取的轉頻成分,使得解調算法依賴于轉速測量設備這一問題,利用CPP估計的IFCF重復計算轉頻,對潛在的轉頻解調,實現了對轉頻相位的估計,擺脫了對轉速計的依賴。
(3) 軸承振動信號中轉頻分量幅值較小,容易被噪聲淹沒,逐步解調濾波算法不僅可以恢復時變信號周期性,還可以有效的濾除噪聲的干擾。

