亞純函數系數微分方程解的復振蕩性質

王騰毅

亞純函數系數微分方程解的復振蕩性質

王騰毅

（貴州財經大學數學與統計學院，貴州，貴陽 550025）

綜合運用Nevanlinna值分布的理論，Wiman-Valiron的理論及其它復分析中的常用方法研究了復域上高階微分方程解帶有小函數時復振蕩的性質，該文的結果將二階情形推廣到高階情形。

亞純函數；微分方程；小函數

1 引言與主要結果

1.1 Nevanlinna值分布理論，Wiman-Valiron的理論簡介

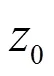
Wiman-Valiron的理論是研究考慮整函數系數微分方程的整函數解性質的一個十分重要的工具。

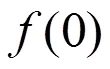
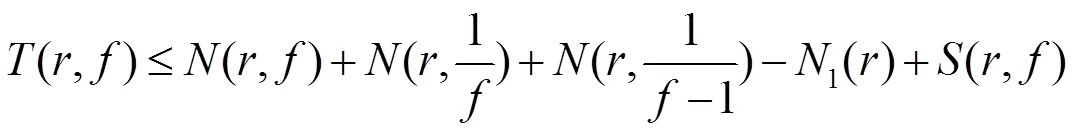
Picard定理：是復平面上的解析函數，并且始終不取值0，1，那么一定是一個常數。

1.2 亞純函數系數微分方程解的復振蕩性質領域的研究現狀

目前主要研究的是二階復域微分方程，對于高階的情況，討論較少。

2006年陳玉研究了二階復域微分方程亞純解的不動點與超級，得到了如下結論：

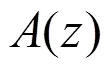
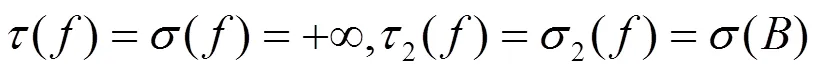
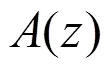
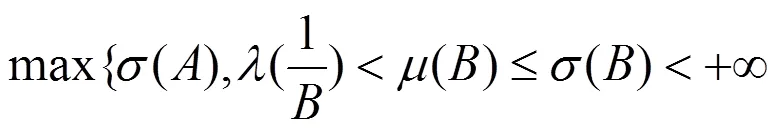
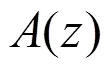
本文研究了一類高階微分方程的亞純解與其小函數的關系得到了如下結論。

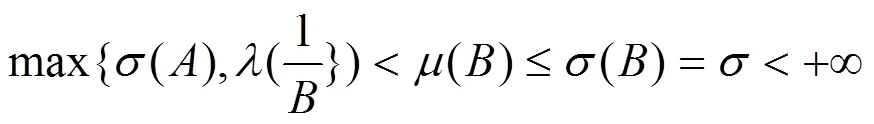
和

至多有一個例外解，其他所有非零解都有無窮多個不動點，且滿足

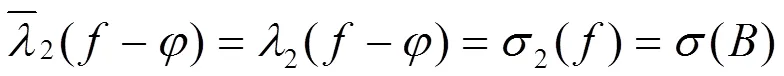
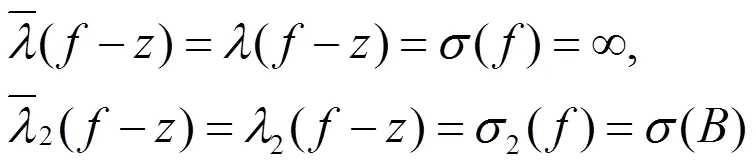
2 定理證明所需引理

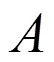
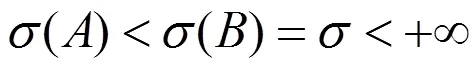
和

則有

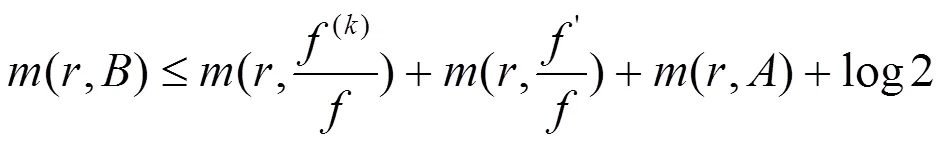
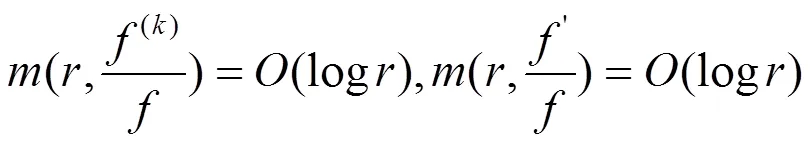
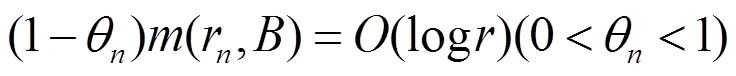
即

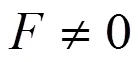
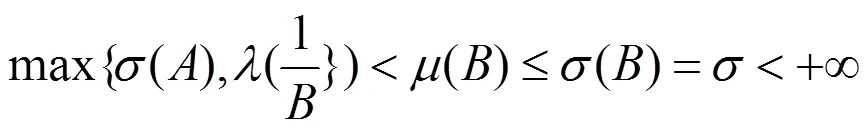
和

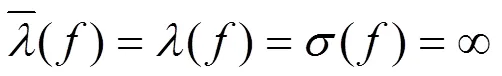
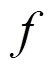
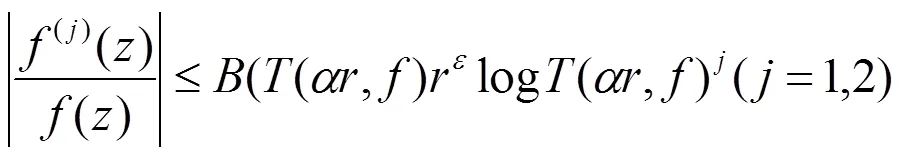
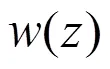
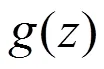
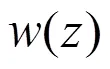
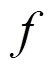
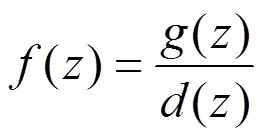
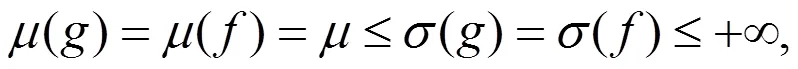
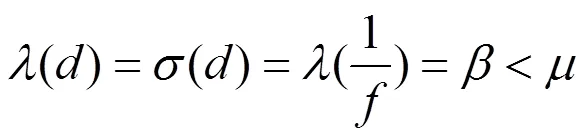
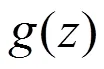
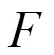
3 定理的證明

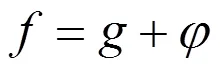
把(5)式代入(1)式并整理后得到

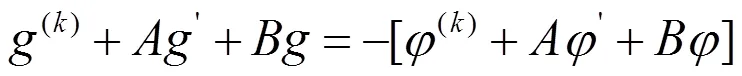
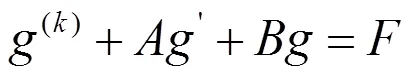
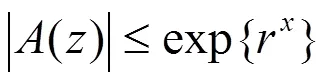
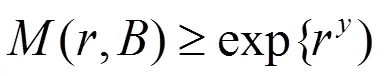
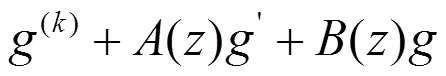
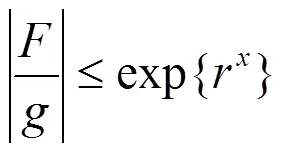
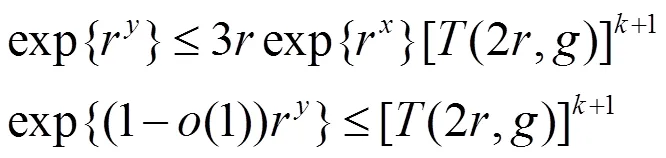
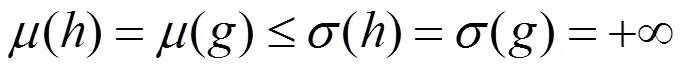
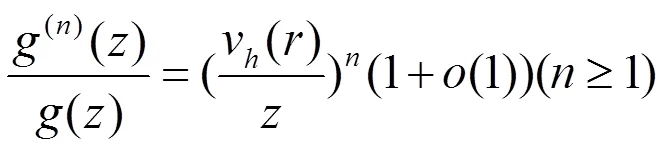
把方程(7)式改寫為

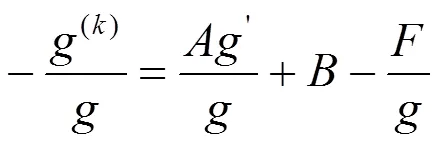
把(14)式代入(15)式有

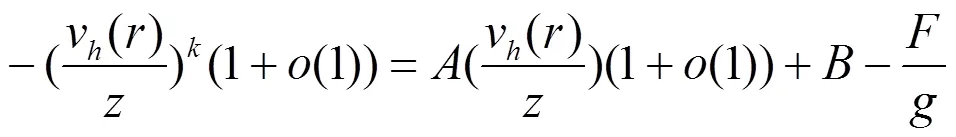
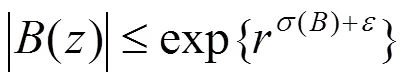
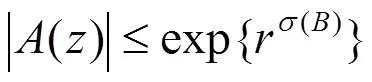
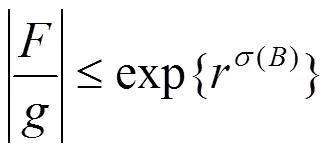
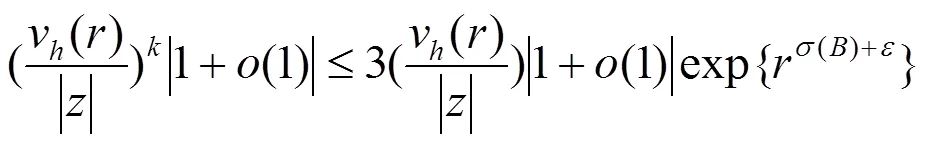
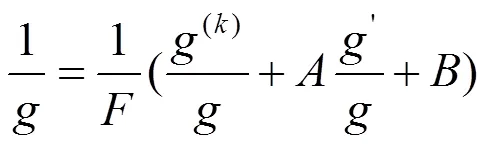
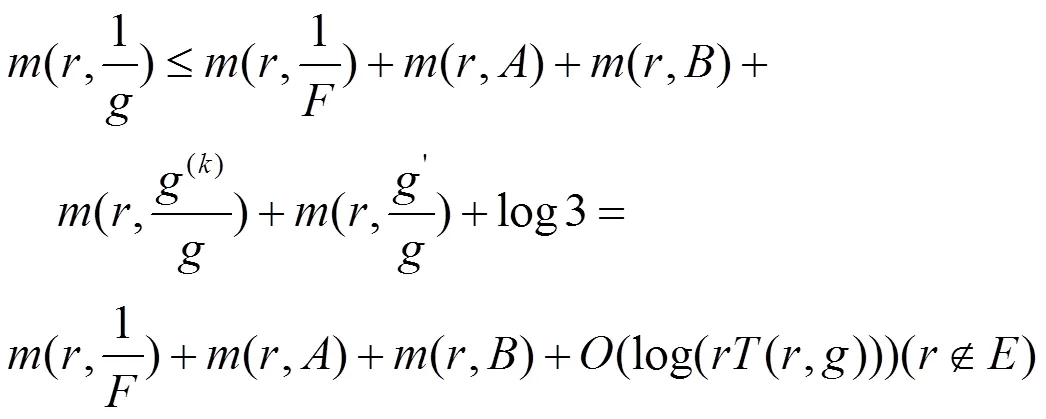
由式(22)及(23)可知

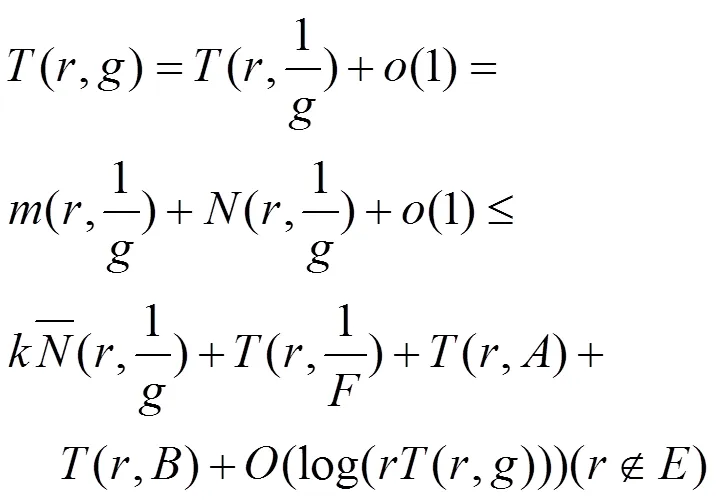
綜上所述

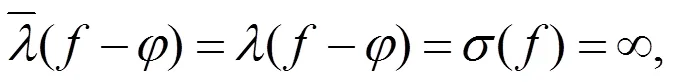
4 總結

本文主要綜合地運用了Nevanlinna值分布的理論，Wiman-Valiron的理論和其它復分析方法研究復數域高階微分方程的解帶有小函數時復振蕩的性質，將二階的情形推廣到高階情形中一種特殊情況，帶有小函數應用的情況，得出了高階情形下定理，并證明結論也成立。

[1] 陳玉,陳宗煊. 二階復……