一道高考函數壓軸題的分析與啟示

顧肖逸

函數作為高中數學內容的一條主線，貫穿于高中數學學習的始終，并在高考中扮演著重要的角色——它常常以壓軸題的形式出現.函數問題憑借其結構形式多變、分類討論情況復雜等特點，成為高中數學學習中的難點之一.那么面對一道函數壓軸題，我們應該如何對其進行分析，從而獲解呢？下面以一道高考函數壓軸題為例，談談我在解決函數壓軸題過程中的學習心得，與各位同學分享.

一、試題呈現

已知函數f（x）＝ex＋e-x，其中e是自然對數的底數.

（1）證明：f（x）是R上的偶函數；

（2）若關于x的不等式mf（x）≤e-x＋m-1在（0，＋∞）上恒成立，求實數m的取值范圍；

（3）已知正數a滿足：存在x0∈［1，＋∞），使得成立.試比較ea-1與ae-1的大小，并證明你的結論.

二、試題的分析與解

1.第一問

第一問比較簡單，可直接利用定義解決.首先，函數f（x）的定義域為R，關于原點對稱，其次又因為f（-x）＝e-x＋ex＝f（x），所以函數f（x）是R上的偶函數.

2.第二問

第二問的分析與解，我采取了以下步驟進行分析：

（1）認知過程一：這是什么問題？

從題干條件不難看出，這是一個典型的恒成立問題.

（2）認知過程二：我以前有沒有處理過類似的問題，如果有，當時是怎么解決的？

可以套用解決恒成立問題的一般方法：參數分離法或構造函數法.

（3）認知過程三：在具體進行操作時，如何選擇合適的方法進行研究？

我在學習和研究函數問題的過程當中，積累了如下的解題經驗：

①一般來說，如果容易分離的就進行參數分離；

②在參數分離之前，可考慮用換元法將問題進行簡化.

由以上的認知過程的分析，我嘗試給出了以下解法：

解法1mf（x）≤e-x＋m-1?m（ex＋e-x）≤e-x＋m-1，在x∈（0，＋∞）上恒成立，即m（ex＋e-x-1）≤e-x-1；令t＝ex（t＞1）；因為1，當且僅當t＝1時，等號成立；

當t＞2時，h′（t）＞0；則當1＜t＜2時，h′（t）＜0；因此可知當t＝2時，h（t）有極小值.

（注：解法1在參數分離后利用導數方法求得函數的最小值.）

解法2由題意知，m（ex＋e-x）≤e-x＋m-1在（0，＋∞）上恒成立，令t＝ex，則t＞1.所以對任意的t＞1恒成立，注意到2＋1＝3，當且僅當t＝2時等號成立，所以，故，因此m的取值范圍為.

（注：解法2在參數分離后利用基本不等式方法求得函數的最小值.）

（4）認知過程四：本題如果利用構造函數的方法進行研究，如何對參數進行分類討論呢？

通過構造函數解決恒成立問題，分類討論是無法避免的，那么如何有效進行參數的分類討論呢？我的體會和經驗是如果要分類討論，一定是產生解題沖突的結果.

比如對于含參的二次函數f（x）＝ax2-2x＋1來說，此時產生的認知沖突是它到底是什么函數？可能是一次函數，也可能是二次函數（開口可向上也可向下），因此需分為a＞0，a＝0，a＜0三種情況討論；再比如函數f（x）＝x2-（a＋1）x＋a，它可以因式分解為f（x）＝（x-1）（x-a），此時產生的認知沖突是其零點的大小，因為需分為a＜1，a＝1，a＞1三種情況討論.以下利用構造函數的方法不難給出本題的解法：

解法3由條件知m（ex＋e-x-1）≤e-x-1在（0，＋∞）上恒成立，令t＝ex（t＞1），則有，對任意的t＞1恒成立.令，

（注：因為分母恒正，分子的正負決定了g′（t）的正負，從而影響函數的單調性，分子部分即是前面所分析的含參的二次型函數，因此先對m＝0，m＞0，m＜0三種情況討論.

（1）當m＝0時，，g（t）在（1，＋∞）上單調遞增，所以g（t）＞g（1）＝m＝0，所以m＝0舍去；

（2）當m＞0時，y＝mt2-m＋1在（1，＋∞）上單調遞增，mt2-m＋1＞1＞0，g（t）在（1，＋∞）上單調遞增，所以g（t）＞g（1）＝m＞0，所以m＞0舍去；

（3）當m＜0時，由，易知g（t）在上單調遞增，在上單調遞減，所以，解得.

3.第三問

第三問的分析與解，可以類比第二問的步驟進行分析：

（1）認知過程一：這是什么問題？

從題干條件不難看出，本題可分解為兩個小問題：

問題1：?x0∈［1，＋∞），使得成立，求參數a的取值范圍.

問題2：利用問題1得到的參數a的取值范圍，比較ea-1與ae-1的大小.

問題1是一個典型的不等式有解問題，問題2則是一個比較代數式的大小問題.事實上，很多函數壓軸題都可以進行這樣的難題分解.將難題進行分解，然后逐一解決，有時即使解決不了最終的問題，但能解決分解后的幾個小問題，從考試來說，也能得到可觀的分數.

（2）認知過程二：我以前有沒有處理過類似的問題，如果有，當時是怎么解決的？

不等式有解問題方法和恒成立問題一致，仍然可考慮參數分離法或構造函數法.

對于比較大小問題，可考慮構造函數的方法解決.

由以上的認知過程的分析，我嘗試給出了以下解法：

難題分解1：?x0∈［1，＋∞），使得成立，求參數a的取值范圍.

分解路徑1（構造函數法）：

令g（x）＝f（x）-a（-x3＋3x），只要在x∈［1，＋∞）上，g（x）min＜0即可.

分解路徑2（參數分離法）：

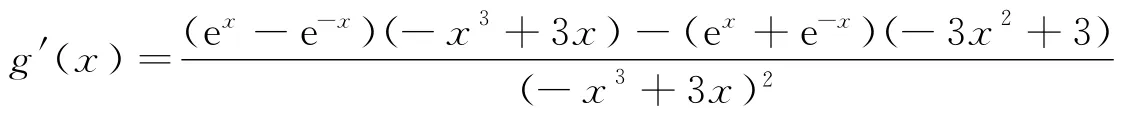
（注：可能會有同學一陣眩暈，別怕，先從函數解析式的角度進行觀察，在定義域上，分子部分是單調遞增的函數，分母部分是單調遞減的函數，且分子和分母均大于0恒成立，g（x）還不是單調遞增嗎？有了這個目標.對接下去的證明工作起了很好的導向作用，通過觀察，我們猜想g（x）是一個單調遞增的函數，那還不應該大于0恒成立嗎？）

難題分解2：如何根據求得的參數a的取值范圍比較ea-1與ae-1的大小？

分解路徑1（取對數后構造函數比大小）：

由于ea-1與ae-1均為正數，同取自然底數的對數，即比較（a-1）lne與（e-1）lna的大小，即比較與的大小.

（注：取對數思想在高考題中的體現可追溯到1992年全國高考題：

（1）已知a，b為實數，且e＜a＜b，其中e是自然對數的底數，證明ab＞ba；

（2）如果正實數a，b滿足ab＝ba，且a＜1，證明：a＝b.）

分解路徑2（變同底，構造函數比大小）：

要比較ea-1與ae-1的大小，由于ae-1＝e（e-1）lna，那么，故只要比較a-1與（e-1）lna的大小.

令h（x）＝（e-1）lnx-（x-1），那么，當x＞e-1時，h′（x）＜0；當0＜x＜e-1時，h′（x）＞0；所以在區間（0，e-1）上，h（x）為增函數；在區間（e-1，＋∞）上，h（x）為減函數.

又h（e）＝0，h（1）＝0，則；那么當時，h（a）＞0，eh（a）＞1，ae-1＞ea-1；當a≥e時，h（a）≤0，0＜eh（a）≤1，ae-1≤ea-1.

三、試題解決的啟發

通過以上的分析，我們不難總結出一些解決函數壓軸題的思路，也同時能獲得一些良好的解決函數問題的活動經驗.

首先，我們對問題進行總體感知，確定問題模型，即明確該問題涉及的基本問題是什么，以及主要的解決方案是什么，從而形成良好的解題結構.以本題為例，本題涉及了高中函數的重要問題：恒成立問題和存在性問題.由此，我們利用解題學習獲得的經驗明確這類問題的解題方向：對函數的最值加以研究，并對命題進行轉化.而對于這兩類問題，常見的研究方法是參數分離法和構造函數法.

其次，對條件的結構加以觀察，選取解決問題的最優方法.以本題為例，在第二問的解決過程中不等式的結構形式較為清晰，容易進行參數分離，參數分離是本題的最優方案，避免了冗雜的分類討論，但在第三問中，結構形式較為復雜，我們傾向于選擇直接構造函數的方法，事實也證明了我們的分析——第三問如果進行參數分離，最后得到的結構比較復雜，容易造成恐慌.因此，在解決問題之前，選擇合適的解題策略也應包含在問題解決的過程之中.

最后，對難題進行分解.綜合題之所以成為綜合題，可能是由多個知識點組合而成的，或是由多個基本題拼湊形成的.對于一些較難的函數問題，當實在啃不動時，一個明智的做法是：可以將它劃分為幾個子問題或一系列的步驟，嘗試去解決問題的一部分，得到相應的得分，從而盡可能提高壓軸題的得分.