探究實根分布問題

江蘇省興化中學 何名慰

一元二次方程實根分布問題的研究，是我們平時研究得比較透徹的一類問題.筆者在過去的一些資料中發現這類問題又被老師們分成了六七個小類，比如有一解、有兩解；兩解都在某區間內、都在某區間外；兩根都大于某個數、都小于某個數、一根大于某數另一根小于某數，等等.

很多同學覺得難以掌握.主要原因在于，不同“類型”的問題，其細節處理有很大不同.有的需要考慮“判別式Δ”，有的需要考慮二次函數對稱軸的范圍，有的只需要考慮區間端點處函數值符號，有的需要考慮的條件明顯更多……一些較為優秀的同學都陷入了背題型的模式.

為什么明明說好的“數形結合”最終演變成讓人萬分頭痛的“背題型”呢？我們需要思考一個問題：“函數的零點”這節課的核心是什么？

當然是零點存在性定理（零點定理）.其核心內容是“若一個函數在某閉區間內連續，且在該區間的兩端點處的函數值異號，則該函數在該閉區間去掉端點后的開區間內必有零點”.

運用好這一定理，在此基礎上合理地運用常規的數學思維方式，我們容易發現一元二次方程實根分布問題根本不會有那么多種題型，其實大家都一樣，都是相同的思維方式.

為了更直接、更方便地研究問題的實質，我們約定，接下來的問題都只研究一元二次方程有兩個不等的實根的情況，不必在重根問題上自找麻煩.

例已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，且x1∈（0，1），x2∈（7，8），求實數a的取值范圍.

解析由函數f（x）的圖象為開口向上的拋物線，且零點x1，x2滿足x1∈（0，1），x2∈（7，8），容易畫出草圖（如圖1）.

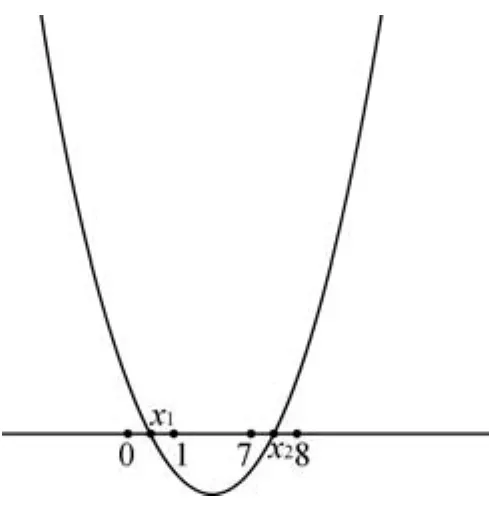
圖1

變式1已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，若x1＜4，x2＞4，求實數a的取值范圍.

變式2已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，若x1＜1，x2＞4，求實數a的取值范圍.

這兩個問題可以類似地解決掉，具體過程不再贅述.這三個問題總結起來就是兩個不等的實根分布在兩個不同的具體的區間內.那么如果兩個不等的實根在同一個區間內呢？上面的方法依然有效嗎？

這才是真正值得研究的部分.

變式3已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，若x1∈（0，4），x2∈（0，4），求實數a的取值范圍.

解析應該充分考慮這個問題與前面問題的關系，不妨設x1＜x2，那么x1應該在開區間0到某數，而x2則在開區間某數到4.那么現在的問題就是：這個“某數”該怎么取才合適？問題到這里已經很明朗了.

我班同學會異口同聲地答“對稱軸x＝a”.結合函數草圖（如圖2），可得

（其中f（a）＜0可以用判別式Δ＞0等價代換）

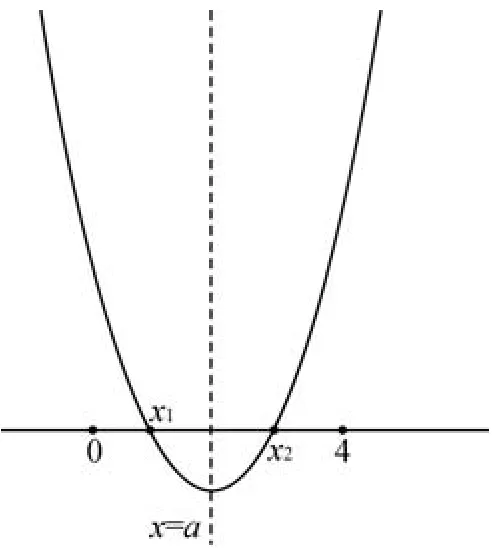
圖2

變式4已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，若x1＜1，x2＜1，求實數a的取值范圍.

該問題實質上可以轉化為兩個不等的零點，一個在區間（-∞，a）內，而另一個在區間（a，1）內（a＜1）.

變式5已知函數f（x）＝x2-2ax＋a＋3有兩個不等的零點x1，x2，若x1＞1，x2＞1，求實數a的取值范圍.

與變式4類似，該問題實質上可以轉化為兩個不等的零點，一個在區間（a，＋∞）內，而另一個在區間（1，a）內（a＞1）.

評價“轉化”是數學思想中最基礎也最重要的一部分，結合二次函數圖象的對稱軸，將不等的兩個實根在一個區間內轉化為由函數圖象的對稱軸分割開的兩個不同的具體區間內，奇妙而又自然.就這么一點小小的轉變，我班同學再也不必因為記憶不同的題型而感到痛苦，他們完全意識到所有的一元二次方程實根分布問題是統一的.解決相關問題必需的知識是零點存在性定理，具體操作的方法是數形結合的方法，結合題中所給條件畫出恰當的二次函數圖象，從而獲得特殊部位函數值的正負，建立相應的不等式（組）.

最后回答開始部分的兩個問題.一、為什么有時候需要考慮對稱軸的范圍？當你遇到的問題中需要用對稱軸將兩個不等的零點“分割”到不同區間時，根據區間的概念（左端點數值小于右端點數值），自然地，對稱軸就有了范圍.二、為什么有時候需要考慮“判別式Δ”的范圍呢？其實判別式Δ對應的是二次函數在對稱軸處的函數值，若二次函數的圖象開口朝上，對稱軸處的函數值為負值，對應的Δ＞0，實質上也是區間端點處函數值的一種正負變化形式.