從必然王國到自由王國

上海 常文武

某年上海市中學生數學知識應用競賽中有一道有趣的題，為了再讓它更有趣些，筆者改編題目如下：

一個圓形的機器人正在一塊邊長為1的正三角形草地內修剪草坪（如圖1）.它的圓形的刀只能在三角形內部貼著草坪的邊緣走，這樣它只能割掉圖中陰影部分.假如你可以調整旋轉刀具的半徑，選怎樣的半徑可以讓鋤草機器人作業面積最大？

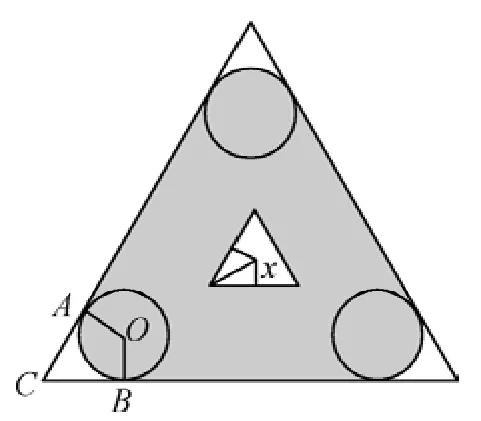
圖1

這個最值問題可以反過來思考，也就是解決三個角上的圖形面積加上中間的三角形面積何時為最小的問題.

設所求的半徑為r，中間正三角形對稱中心到一邊的高為x.

記三角形每個角處留下的非陰影面積為S尖，它可以方便地由四邊形AOCB減去扇形OAB得到：

而x可以通過大三角形的外心到某一邊的距離值（內切圓的半徑）減去2r得到：x＝.從而內部小三角形的面積可算得為：

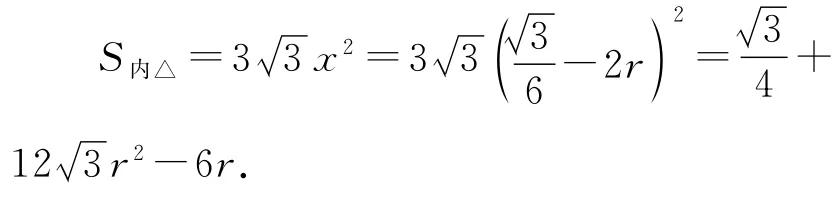
至此，我們希望總和最小的4塊面積S空可以寫作是r的一個二次三項式：

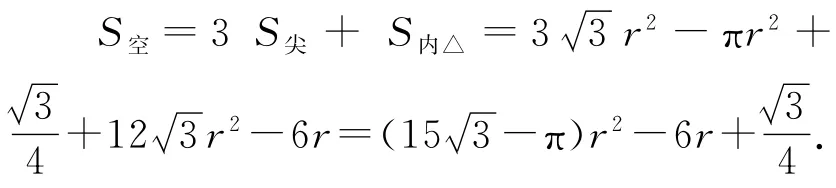
利用二次函數y＝ax2＋bx＋c的頂點坐標公式，這個二次三項式的最小值應該在時達到，即

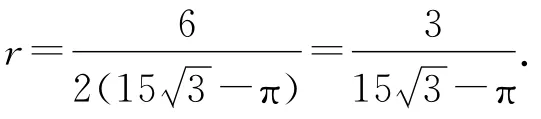
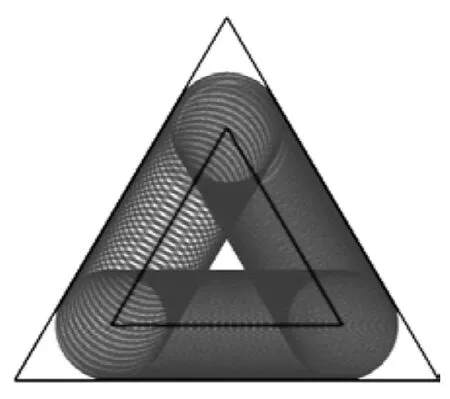
圖2

圖2就是按照這個半徑畫出的效果圖.

題目解完了，我們擱筆思忖，覺得中間這個洞似乎不夠完美.難道一定要留這個洞不成？

確實是這樣的.如果我們確保中間地帶不留空白，那就要增大半徑r的值，三個角的空白也就會隨之增大.顯然當x＝0，也就是r＝時，既確保了中間地帶不留空白，又使得三個角的留白最小.將此r代入S空公式計算發現，空白總和并不是最小的.這也在情理之中，因為中間的空在消失的瞬間，可以認為是保留著一個邊長為0的正三角形.所以可以沿用前面分析的過程.

現在我們真的可以自信滿滿地說，我們找到了問題的答案.且慢！我們雖然從考官那里得了個滿分，但是這道題仍有可挖掘的“寶藏”.我們可以試著改變一下問題的條件.

比如，如果這塊三角形草地是一塊不規則的任意的三角形，問題該怎么解呢？

一塊三角形草地的邊長分別是a，b，c.一個圓形的機器人在為它修剪草坪.它的圓形的刀只能在三角形內部貼著草坪的邊緣走，這樣它只能割掉如圖3所示的陰影部分.假如你可以調整旋轉刀具的半徑，選怎樣的半徑可以讓鋤去的草地面積最大？

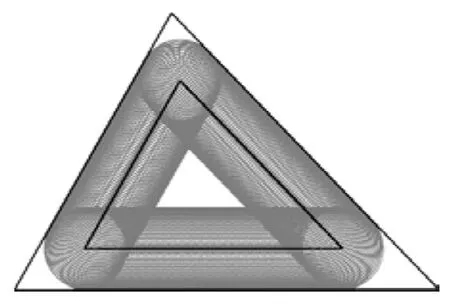
圖3

顯然，新問題比原問題更難些.原來的求解思路考慮到等邊三角形的特殊性.但是，我們發現圓心的軌跡是一個三角形，它與草坪的輪廓是相似的.而且，如果中間有空隙的話，空隙也是一個三角形.顯然，這三個三角形是內心重合、彼此相似的.

由相似三角形面積比是內切圓的半徑之比的平方知，我們需要算出草坪三角形和機器人圓心軌跡三角形的內切圓半徑，顯然二者相差一個機器人半徑r；草坪三角形面積和內部的空白三角形的內切圓半徑，兩者相差兩個機器人半徑2r.

利用內切圓半徑之比也為相似比以及相似三角形面積比等于相似比的平方，可以算出角上的空白區域拼成的三角形（不難想象它的存在）面積為，因此，.

這樣，我們所關心的能割到的區域面積就是：

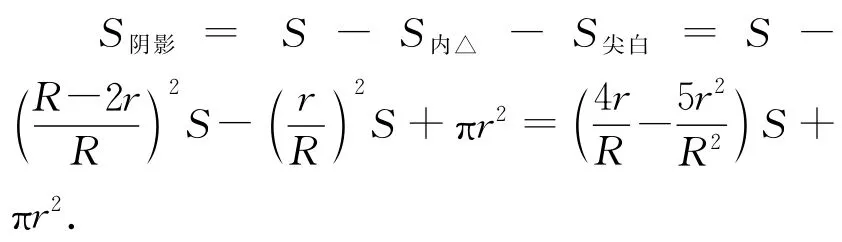
由于三角形內切圓半徑R和半周長p乘積等于面積，即S＝pR，由此，.得

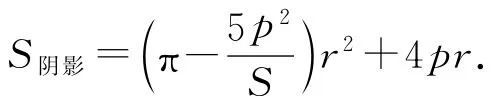
仍然利用二次函數y＝ax2＋bx＋c的頂點坐標公式，這個二次三項式的最大值應該在時達到，即

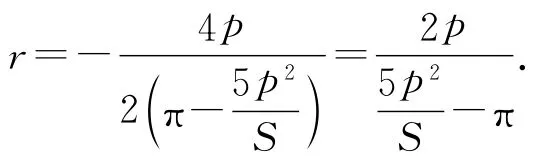
最后，我們需要用三角形的三邊長表示其面積S.套用海倫公式：

經過這番推廣，我們發現從一個小問題的解決可以發展到一類問題的解決辦法.一位哲學家說過，當我們掌握了真理，就可以從一個必然王國到達一個自由王國.誠哉斯言！你可愿繼續探索——掙脫三角形的束縛，研究更自由的凸四邊形情況呢？假定凸四邊形ABCD的四條邊分別長a，b，c，d，并且它還是一個有內切圓的四邊形.可以料想到方法是類同的，當作是餐后的“甜點”吧！