一種三角換元的代數形式及其應用

■江西省豐城中學 吳愛龍 聶燕鳳

在一定條件下,求二元函數的最值問題時,常遇到形如a+b=1,a＞0,b＞0之類的約束條件,聯想到三角中的同角三角函數的基本關系式sin2θ+cos2θ=1,可令a=cos2θ,于是有但由于其中涉及新教材中早已刪了的同角三角函數的其他三角關系secθ·cosθ=1,cscθ·sinθ=1,1+tan2θ=sec2θ,1+cot2θ=csc2θ,又注意到tanθ·cotθ=1,于是我們可以將上述變換改進為代數形式：令,其中x＞0,y＞0,且xy=1,這樣應用起來就沒有超綱之嫌了。

下面列舉數例說明其應用。

1.直接作出代換

例1(2018屆鎮江高三卷)已知a,b為正數,且,則的最小值為__。

解析：令,其中x＞0,y＞0,且xy=1,則a=1+x,b=1+y。

所以：

例2(2019屆無錫高三期中)設x,y為正實數,且=1,則xy的最小值為__。

解析：令其中a＞0,b＞0,且ab=1。

于是x=4a+3,y=3b+1。

例3(2019屆徐州高三期中)已知正實數a,b,并且滿足a+2b=1,則的最小值為__。

解析：令,其中x＞0,y＞0,且xy=1。于是：

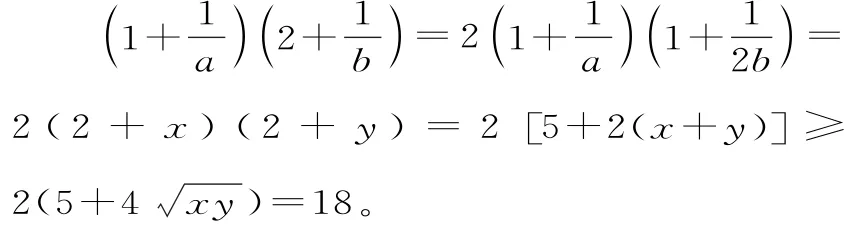
點評：此類題型題設條件很明顯,較易聯想,作出變換,運用二元均值不等式便可迅速得出答案。

2.稍變形,再代換

例4(2016年廣東省高中聯賽預賽)若正數x,y滿足x+3y=5xy,則3x+4y的最小值為__。

解析：由題設知,其中a＞0,b＞0,且ab=1,則

例5(2017年蘇州、無錫、常州、鎮江二模)已知a,b均為正數,且ab-a-2b=0,則的最小值為__。

解析：因為ab-a-2b=0,所以=1。令,其中x＞0,y＞0,且xy=1,則于是：

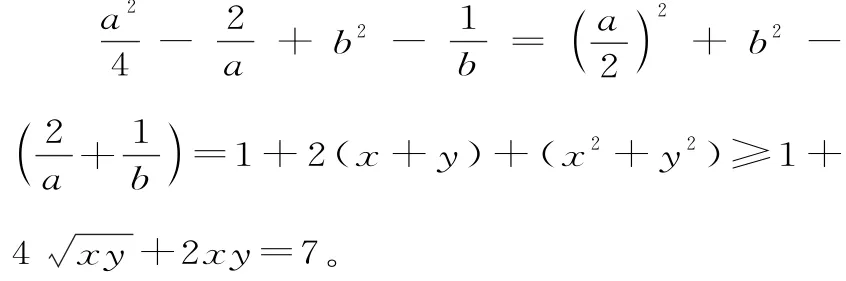
點評：此類題型只要對題設條件稍作變形,亦可快速作出代換,準確得出答案。

3.巧變形,妙代換

例6(2019屆鎮江高三期中)已知x的最小值為__。

解析：由題設知,其中a＞0,b＞0,且ab=1。于是：

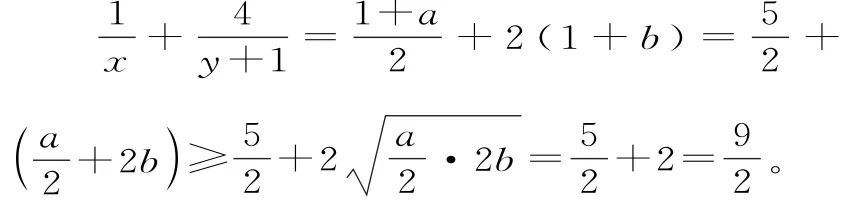
例7(2019屆揚州高三期中)已知正實數a,b滿足2a+b=3,則的最小值是__。

解析：整理得又由題設知2a+(b+2)=5,即,其中x＞0,y＞0,且xy=1,則

例8(第26屆“希望杯”)若正數a,b滿足2a+b=1,則的最小值是__。

解析：由題設知令,其中x＞0,y＞0,且xy=1,則

點評：此類題型題設條件看似簡單,但必須結合目標函數,先適當變形,再作出巧妙代換,解法靈活,難度稍大。

4.先化歸,后代換

例9已知函數,若f(x1)+f(2x2)=1,則f(x1+2x2)的最小值為( )。

解析：將原函數變形為f(x)=1-因為f(x)+f(2x)=1,所以12

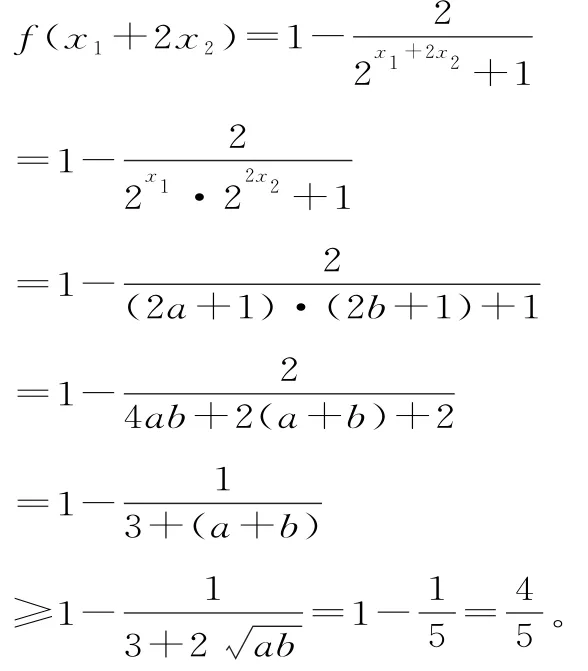
當且僅當a=b=1,即x1=log23,x2=時,f(x1+2x2)的最小值為,選B。

點評：這是一個以指數函數為背景的二元函數最值問題,必須將其轉化為文中所述類型后再作出代換解之。

必須指出,二元函數條件最值問題大都還有別的解法,但通過上述諸例可以看出,該種變換往往能將復雜的目標函數化得較為簡單,甚至能揣摩出目標函數的構建或設計過程,所以解法也就自然顯得更為簡捷或重要了。