高慧明老師講數學（3）
——空間向量的妙用（下）

■北京市第十二中學 高慧明

(接上期)

例4如圖9,四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為梯形,AB∥DC,∠ABC= ∠CAD=90°,且 PA=AB=BC,點E是棱PB上的動點。

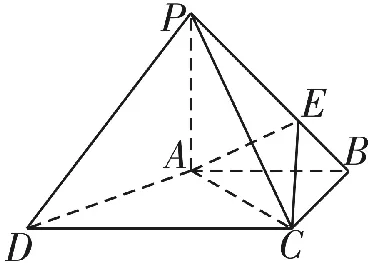
圖9

(1)當PD∥平面EAC時,確定點E在棱PB上的位置;

(2)在(1)的條件下,求二面角A-CE-P的余弦值。

分析：此題的第(2)問是求解二面角的平面角的余弦值,可以用傳統幾何法確定二面角平面角是哪一個角(方法一),但分析及證明過程稍顯復雜,對空間直觀想象能力要求較高;若用空間向量解決(方法二),只需確定平面ACE和平面PCE的法向量,借助兩個法向量的夾角求出二面角平面角的大小(或指定三角函數值)。

解析：(1)在梯形ABCD中,由AB⊥BC,AB=BC,得

因為PD∥平面EAC,又平面EAC∩平面PDB=ME,所以PD∥EM。

圖10

(2)(方法一)如圖11,在等腰直角△PAB中,取PB中點N,連接AN,則AN⊥PB。

圖11

因為平面PAB⊥平面PCB,且平面PAB∩平面PCB=PB,所以AN⊥平面PBC。

在平面PBC內,過N作NH⊥直線CE于H,連接AH。

由AN⊥CE,NH⊥CE,得CE⊥平面ANH,故AH⊥CE。

所以∠AHN就是二面角A-CE-P的平面角。

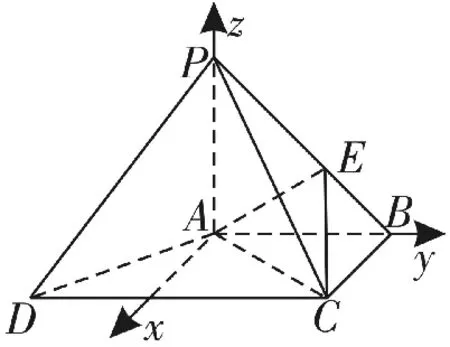
圖12

(方法二)以A為原點,AB,AP所在直線分別為y軸、z軸,如圖12,建立空間直角坐標系。設PA=AB=BC=a,則A(0,0,0),B(0,a,

設n1=(x,y,1)為平面EAC的一個法向 量,則所以解得,所以n1

設n2=(x',y',1)為平面PBC的一個法向量,則得x'=0,y'=1,所以n2=(0,1,1)。

點評：利用空間向量求解二面角平面角大小(或指定三角函數值)的常用策略為：

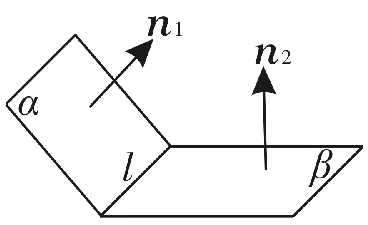
圖13

構造二面角α-l-β的兩個半平面α、β的法向量n1,n2,則：

(1)若二面角α-l-β與法向量n1,n2的位置關系如圖13所示,那么二面角的平面角大小θ等于兩法向量n1,n2的夾角的補角,即cosθ=

(2)若二面角α-l-β與法向量n1,n2的位置關系如圖14所示,那么二面角平面角大小θ等于兩法向量n1,n2的夾角,即

例5如圖15,在四棱錐P-ABCD中,底面四邊形ABCD是菱形,對角線AC與BD交于點O,PA=PC=AC。

(1)求證：平面PAC⊥平面PBD;

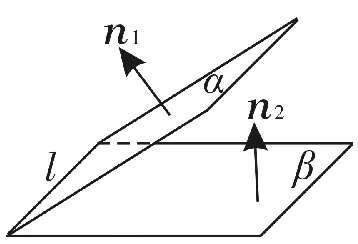
圖14

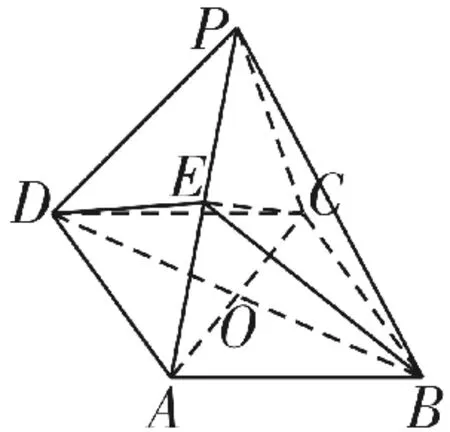
圖15

分析：(1)利用題中條件首先證得線面垂直,然后根據面面垂直的判定定理即可證得結果。(2)結合題中結論,利用勾股定理證得PO⊥平面ABCD,然后在此基礎上建立空間直角坐標系,求出平面BDE和平面CDE的法向量,進而求得二面角B-DE-C的余弦值。

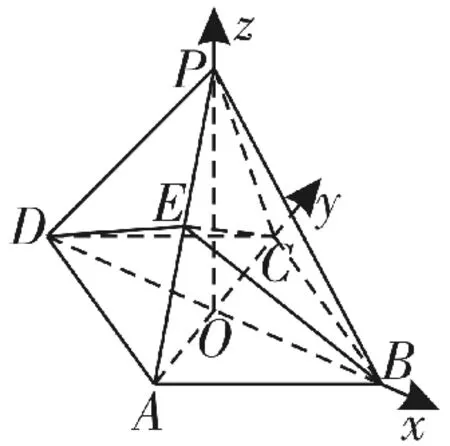
圖16

解析：(1)如圖16,連接PO。在菱形ABCD中,O是AC的中點,且AC⊥BD。

因為PA=PC=AC,所以在△PAC中,PO⊥AC。

又PO∩BD=O,PO,BD?平面PBD,所以AC⊥平面PBD。

又AC?平面PAC,所以平面PAC⊥平面PBD。

因為O是BD的中點,PD=6,所以在△POD中,PD2=PO2+OD2,所以PO⊥BD。

又因為AC∩BD=O,AC,BD?平面ABCD,所以PO⊥平面ABCD。

以O為坐標原點,分別以OB,OC,OP所在直線為x軸,y軸,z軸,建立如圖16所示的空間直角坐標系O-xyz。由題知,A(0,

設n=(x1,y1,z1)是平面BDE的一個法向量

設m=(x2,y2,z2)是平面CDE的一個法向量,則即所以m=(-1,

點評：在利用空間向量解決問題時,若立體圖形的垂直關系不明顯,則在建立空間直角坐標系之前,要先對空間直角坐標系所需涉及的垂直關系的合理性加以證明。如本題,只有底面的AC⊥BD,并沒有出現三條直線兩兩垂直,此時就需要先證明PO⊥平面ABCD,再建立空間直角坐標系。

三、借助空間向量確定幾何元素（通常為點）的確切位置

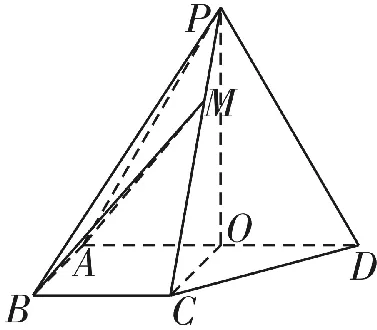
圖17

例6 如圖17,四棱錐P-ABCD中,側面PAD為等邊三角形,且AB=BC=90°,PC=AD,O為AD中點。

(1)證明：PO⊥ 平面ABCD;

分析：(1)結合已知條件,利用線面垂直的判定定理證得結果。(2)利用(1)的結論,建立空間直角坐標系。要確定M點的位置,只需借助點M在PC上,將M點的空間坐標設出(含參數λ),然后利用空間向量的方法表示出二面角M-AB-D的余弦值,進而求得λ。

解析：(1)如圖17,連接OC、OP,因為△PAD為等邊三角形,所以PO⊥AD。

設AB=1,則AD=2,PO=3,PC=2,OC=1,故PO⊥OC。

又PO⊥AD,OC∩AD=O,所以PO⊥平面ABCD。

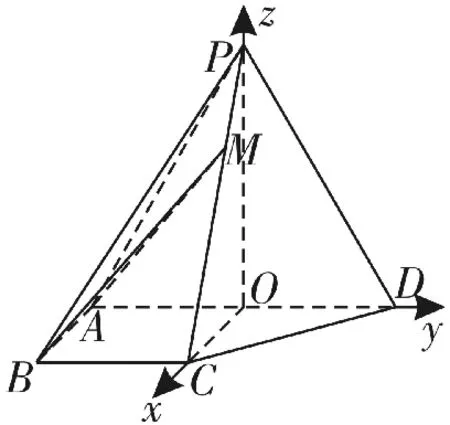
圖18

(2)分別以OC,OD,OP為x,y,z軸建立空間直角坐標系,如圖18。

設BC=1,則P(0,0,3),A(0,-1,0),B(1,-1,0),C(1,0,0)。

點評：對于此類確定(探索)點的位置的問題,通過借助空間向量來確定幾何元素(通常為點)的確切位置,只需在用空間向量描述幾何關系之前引入未知量(一般為點分線段所成的比,比如本例中的λ),然后通過題中條件建立等量關系,得出關于未知量的方程,求解得出未知量。

例7如圖19,在四棱錐S-ABCD 中,底 面ABCD是直角梯形,側棱SA⊥底面ABCD,AB垂直于AD和BC,M為棱SB上的點,SA=AB=BC=2,AD=1。

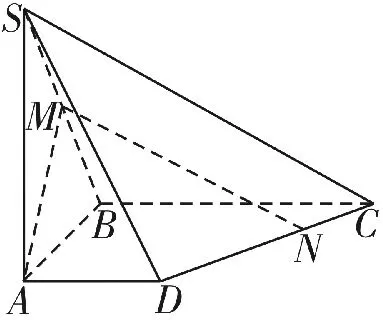
圖19

(1)若M為棱SB的中點,求證：AM∥平面SCD;

(2)當SM=2MB時,求平面AMC與平面SAB所成的銳二面角的余弦值;

(3)在(2)問條件下,設點N是線段CD上的動點,MN與平面SAB所成角為θ,求當sin

θ取最大值時點N的位置。

分析：(1)利用中位線定理與線面平行的判定定理證得AM∥平面SCD;(2)利用SM=2MB,表示出M點的坐標,分別求得平面AMC與平面SAB的法向量,利用求得結果;(3)設出N點的坐標,求出直線MN的方向向量和平面SAB的法向量,然后利用sinθ取得最大值時與x的關系,求得x,從而確定N的位置。

解析：(1)如圖20,取線段SC的中點E,連接ME,ED,在△SBC中,ME為中位線,所以ME∥BC,又AD∥BC,所以ME∥AD,所以四邊形AMED為平行四邊形,所以AM∥DE,又DE?平面SCD,AM?平面SCD,所以AM∥平面SCD。

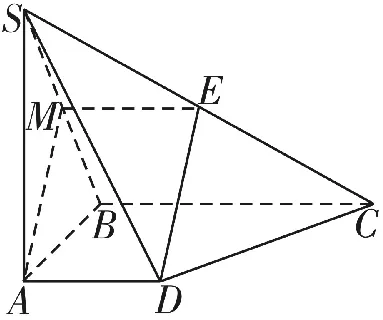
圖20

(2)以點A為坐標原點,分別以AD,AB,AS為x,y,z軸,建立如圖21所示的空間直角坐標系,則A(0,0,0),B(0,2,0),C(2,2,0),D(1,0,0),S(0,0,2),由條件得M為線段SB接近B的三等分點。

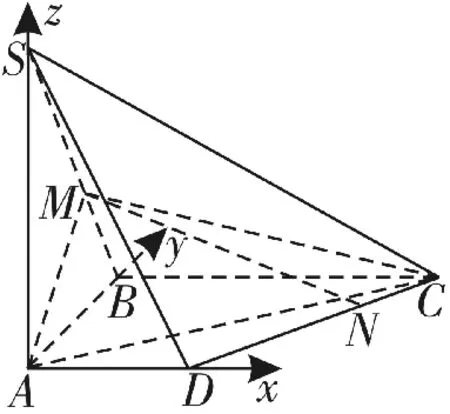
圖21

將坐標代入得n=(-1,1,-2),另外易知平面SAB的一個法向量為m=(1,0,0)。

(3)設N(x,2x-2,0),其中1＜x＜2,由 于M所 以

(續完)