淺析導數應用中的幾種數學思想

■安徽省利辛高級中學 胡 彬

數學家華羅庚先生說過：數學是一個原則,無數內容,一種方法,到處可用。數學思想是高中數學的靈魂,也是數學知識的精髓。在學習導數的過程中,同學們若能靈活運用相關的數學思想,往往能迅速、準確地找到解題思路,從而獲解。

一、函數思想

函數思想是用運動和變化的觀點去分析和研究數學問題中的數量關系,是對函數概念的本質認識。它是先建立函數關系或構造函數,再運用函數的圖像和性質去分析問題、轉化問題,最后使問題獲得解決的一種數學思想。導數問題蘊含著函數思想,解題時若能靈活運用這種思想,就能使問題順利解決。

例1設函數f(x)滿足x2f'(x)+,則x＞0時,f(x)( )。

A.有極大值,無極小值

B.有極小值,無極大值

C.既有極大值又有極小值

D.既無極大值也無極小值

解析：由題意知令g(x)=ex-2x2f(x),則g'(x)=ex-2x2f'(x)-4xf(x)=ex-由g'(x)=0,得x=2。當0＜x＜2時,g'(x)＜0,g(x)單調遞減;當x＞2時,g'(x)＞0,g(x)單調遞增。故g(x)min=g(2)=0。則當x＞0時,f'(x)≥0,故f(x)在x∈(0,+∞)上單調遞增,既無極大值也無極小值,應選D。

評注：通過構造函數g(x),運用函數g(x)的函數性質,從而得到x＞0時,f(x)單調遞增。

二、方程思想

方程思想就是分析數學問題中變量間的等量關系,建立方程或方程組,或構造方程,再通過解方程或方程組,或者運用方程的性質去分析、轉化問題,使問題獲得解決。

例2若函數f(x)、g(x)分別為R上的奇函數、偶函數,且滿足f(x)-g(x)=ex,則有( )。

A.f(2)＜f(3)＜g(0)

B.g(0)＜f(3)＜f(2)

C.f(2)＜g(0)＜f(3)

D.g(0)＜f(2)＜f(3)

解析：對于f(x)-g(x)=ex,以-x代替x得到f(-x)-g(-x)=e-x。又f(x)為奇函數,g(x)為偶函數,所以上式可化為-f(x)-g(x)=e-x,從而則0恒成立,所以f(x)在定義域R上為增函數,0=f(0)＜f(2)＜f(3)。又g(0)=-1＜0,所以g(0)＜f(2)＜f(3),應選D。

評注：先挖掘條件,再建立方程。

三、數形結合思想

數形結合思想是數學中重要的思想方法,許多導數問題可借助于平面直角坐標系,將數的問題轉化為形的問題,從而借助于形的優勢,使問題獲解。

例3已知函數若函數g(x)=f(x)-a有3個零點,則實數a的取值范圍是( )。

解析：當x＜0時,f(x)=-(x+1)ex。f'(x)=-(2+x)ex,由f'(x)＞0,得x＜-2;由f'(x)＜0,得x＞-2。所以f(x)在(-∞,-2)上遞增,在(-2,0)上遞減,故且x＜-1時,f(x)＞0,畫出y=f(x)的圖像如圖1所示。由圖知當時,y=f(x)與y=a的圖像有3個交點,即g(x)有3個零點,所以實數a的取值范圍是,應選A。

評注：形如f(x)=h(x)-g(x)的零點問題常轉化為兩函數y=h(x)與y=g(x)的圖像交點問題,然后利用數形結合求解。

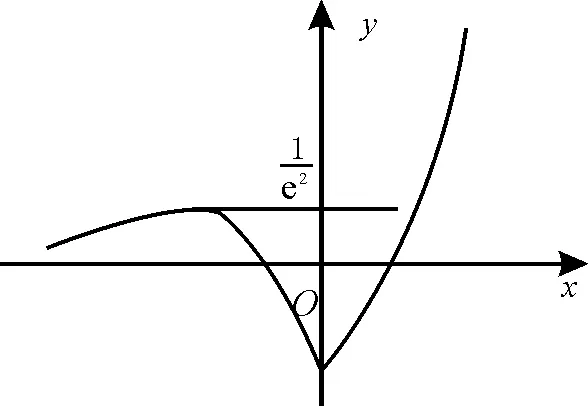
圖1

四、分類討論思想

分類討論就是將數學對象劃分為不同種類,再分別進行研究或求解的一種數學思想。通過合理的分類討論,可以使較復雜的問題簡單化。

例4設函數f(x)=1+(1+a)x-x2-x3,其中a＞0。

(1)討論f(x)在其定義域上的單調性;

(2)當x∈[0,1]時,求f(x)分別取得最大值和最小值時對應的x的值。

解析：(1)f(x)的定義域為(-∞,+∞),f'(x)=1+a-2x-3x2,令f'(x)=0,得x1

所以f'(x)=-3(x-x1)(x-x2)。

當x＜x1或x＞x2時,f'(x)＜0;

當x1＜x＜x2時,f'(x)＞0。

故f(x)在(-∞,x1)和(x2,+∞)上單調遞減,在(x1,x2)上單調遞增。

(2)因為a＞0,所以x1＜0,x2＞0。

①當a≥4時,x2≥1,由(1)知,f(x)在[0,1]上單調遞增,所以f(x)在x=0和x=1處分別取得最小值和最大值。

②當0＜a＜4時,x2＜1,由(1)知,f(x)在[0,x2]上單調遞增,在[x2,1]上單調遞減,因此f(x)在處取得最大值。

又f(0)=1,f(1)=a,所以當0＜a＜1時,f(x)在x=1處取得最小值;當a=1時,f(x)在x=0和x=1處同時取得最小值;當1＜a＜4時,f(x)在x=0處取得最小值。

評注：本題考查利用導數求函數的單調區間和最大(小)值,同時考查分類討論的思想,分類討論的關鍵是確定分類的標準。

五、轉化與化歸思想

轉化與化歸思想是一種重要的數學思想方法,在研究、解決數學問題時,當思維受阻或遇到困難的問題時,要善于轉化問題,化難為易,化繁為簡,化陌生為熟悉,即轉化到另一種情境使問題得到解決,這種轉化是解決問題的有效策略。

例5設x3-x2-3。

(1)如果存在x1、x2∈[0,2]使得g(x1)-g(x2)≥M成立,求滿足上述條件的最大整數M;

解析：(1)存在x1、x2∈[0,2]使得g(x1)-g(x2)≥M成立,等價于[g(x1)-g(x2)]max≥M。因為g(x)=x3-x2-3,所以。由g'(x)＞0,得x＜0或;由g'(x)＜0,得0＜x＜。又x∈[0,2],所以g(x)在上是單調減函數,在上是單調增函數。解得所以=1。故[g(x1)-g(x2)]max=g(x)max-所以滿足條件的最大整數M=4。

min≥g(x)max。由(1)可知在上,g(x)max=g(2)=1。在≥1恒成立,等價于a≥x-x2lnx恒成立。

設h(x)=x-x2lnx,則h'(x)=1-2xlnx-x,可知h'(x)在上為單調減函數。

因此,函數h(x)=x-x2lnx在上單調遞增,在[1,2]上單調遞減。

所以h(x)max=h(1)=1,即a∈[1,+∞)。

評注：審題時需要深刻理解題意,對問題作等價轉化,即f(x)≥g(a)對于x∈D恒成立,應求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,應求f(x)的最大值。