淺析課堂追問的技巧

顧向紅 李衛星

[摘 ?要] 追問是教師預設發問的延伸，更是提升教師教學質量的有效途徑. 在課堂教學中，有效的追問，可以讓學生形成自主發散思維能力，培養學生的數學素養. 文章就初中課堂中教師有效追問的時機提出可行建議，以期達到提高課堂有效性的作用.

[關鍵詞] 初中數學;課堂教學;提問;追問

在課堂教學中，提問作為溝通教師、學生以及教材的橋梁，既是教師有效的教學手段，又是激發學生深入思考的有效途徑. 教學中的“問”可謂大有學問，“問”得恰到好處，可以啟迪學生思維，培養學生素養. 而教學中的“追問”作為課堂提問的精華，也就是在學生回答教師的預設問題的基礎上，教師有意識地再次提問，促進學生發散或聚合型思維的養成 .[1]

追問于認知沖突之處——云開見日

在新知識的學習中，學生由于受已有知識經驗的影響，會出現思維障礙又或是認知矛盾，無法透過現象看到本質，思考、分析或解釋停止. 這時教師需充分發揮追問的優勢，引導學生突破、分化難點，從而啟迪學生的思維.

案例1？搖 以“梯形的復習課”的教學片段為例

教師首先拋出一個問題：已知一個梯形ABCD，現在請你作一條直線將其分為面積相等的兩個部分？由于這一問題的提出略顯“唐突”，學生思維出現“卡殼”的情況. 這時，教師則展開了對問題的追問，從而激活學生的思維，將學生的思考領向更高層次.

師：那我們首先思考，在已學的三角形中，我們是如何通過一條直線將其分為面積相等的兩個部分的呢？

生1：這個很簡單，我們可以通過作這個三角形的中線，以這條直線來平分三角形面積.

師：很好！那平行四邊形呢？

生2：可以根據平行四邊形的中心對稱入手，作經過它對角線交點的任意一條直線，以這條直線平分平行四邊形面積.

師：非常正確，那現在我們思考一下，在梯形這一內容的學習過程中，我們如何解決梯形問題呢？

生3：我知道，我們一般就是將它特殊化，要么轉化為平行四邊形，要么轉化為三角形，這樣解決起來容易多了.

師：不錯，一般涉及梯形問題，我們都需要轉化，但借助哪些常用輔助線呢？

生4：一般做法是，平移它的一腰，然后連結梯形的頂點與它一腰的中點并延長與底邊相交......

生5（異常興奮地）：我想到了一種方法，我們從梯形面積公式入手，分別取兩底邊的中點，并連結.

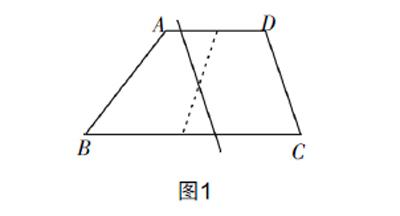
生6：如圖1所示，我認為可以分別取梯形ABCD兩底邊的中點并連結，而后取這一線段的中點，這一點與上底邊相交的無數條直線都可以.

生7：如圖2所示，我們可以作輔助線將梯形轉化為平行四邊形，所有過平行四邊形對角線交點的直線都可平分梯形面積.

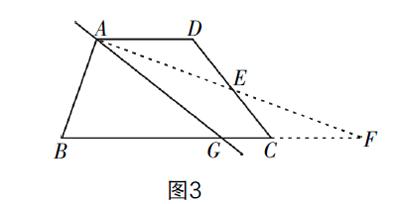
生8：如圖3所示，我們可以作輔助線將梯形轉化為三角形，三角形的中線所在的直線平分梯形.

這一案例意在引導學生鞏固梯形知識，深化梯形特征. 教師充分利用了學生的認知沖突，從追問入手，層層遞進式切入主題，逐步引領學生自然找到解決問題的“出口”，從而達到解決問題的最佳路徑，學生通過這樣數學化的過程，逐步接近問題本質，逐步獲得對知識的理解，這也是追問的價值所在.

追問于錯誤之處——迷而知反

最真實的課堂才是理想的課堂. 因此，在課堂教學中呈現這樣或那樣的錯誤是司空見慣的. 教師需要善待這些錯誤，用心解讀錯誤的本質，有效把握糾錯的時機，采取行之有效的方法引導和點撥學生，對學生的錯誤實施追問，引發學生深度思考和深入討論，讓學生在思考和反思中認識和糾正錯誤.

案例2 以“反比例函數的性質”的教學片段為例

師：好了，老師就講到這里，那么下面哪位同學來歸納一下反比例函數的性質！

生1：當k>0時，y隨x的增大而減小.

師：你們認為他總結得準確嗎？

生（有的點頭，有的陷入沉思）

師：那么，下面根據生1的總結，我們一起來判斷“已知反比例函數y= ，x=2以及x=-2時對應y值的大小關系如何？”

生（立刻進入口算狀態，并發現生1的總結存在問題）

師（拾級而上）：那有沒有人能稍做修改呢？

（學生們都認識到這一表述的問題所在，但都無法完整組織語言進行描述，一個個面面相覷. ）

師（再次追問）：那我們利用數形結合的思想再結合圖像進行觀察，是否存在著什么問題呢？

學生經過思考和驗算，很快找到錯誤的根源，從教師的例子中可以觀察出這兩個點并不位于同一象限. 因此，學生很快糾正了錯誤“條件的遺漏”.

由此可見，學生的錯誤都是具有價值的，是學生真實經驗的反映，更是鮮活的可生成性資源，教師的準確辨別和努力挖掘可以讓錯誤資源“增值”，可以讓課堂效率“增效”.

追問于深度不足之處——追求深度

追問教學是具有深度的，通過“問題串”去層層推進，或引發認知沖突、或釋疑，從而將問題引向深度，引向本質. 在這一步步逼近本質的追問中，學生習得過硬的知識技能，指向思維深度，并錘煉自身的意志品質.

案例3？搖以“復習翻折問題”的教學片段為例

問題：如圖4所示，已知矩形紙片ABCD，現沿著折痕AE折疊使B點與F點重合，此時四邊形ABEF是什么圖形？請證明.

由于這一問題難度較小，不少學生很快就能從鄰邊相等的矩形出發，求證得出四邊形ABEF為正方形.

師：大家都求證得很準確，現在再思考一下，如圖5所示，若沿著EG折疊使C點與EF上的H點重合，這時又有何發現呢？

生1：可證四邊形CEHG也為正方形.

生2：AE⊥EG.

師（追問）：若如圖6所示，點F落于矩形ABCD內，AE⊥EG還成立嗎？請證明.

（學生進行了討論，并解決了這一問題.）

師：經過上面一系列思考，能否講一講翻折問題的本質？我們在解決翻折問題時，應以哪些知識或方法為出發點？下面先獨立思考，然后小組討論交流.

生3：其本質應該是軸對稱，我們在解決翻折問題時，首先要以其中不變的線段或角度為突破口來解決問題.

生4：如果在翻折問題中需求線段的長度，還需用到勾股定理或相似三角形的知識點.

師：說得真好！我們課后再思考一下，剛才的問題是否還能與其他知識點之間建構聯系呢？

顯然，以上的教學片段不僅僅是釋疑的過程，而是通過不斷變換問題，引導學生從現象到本質認識問題，讓學生真正感受思考過程的真實、深刻、豐富和生動，從而提高學生的思維能力.

追問于意外之處——精彩生成

課堂不應該是按照“教學攻略”行走的毫無激情的過程，而應該是朝著未知方向前進的一段旅程，在旅途中隨時都有意外的風景和完美的收獲. 因此，課堂應該是隨時都會發生意外的，當這些富有價值的意外出現時，教師若能積極回應，則可以充分發揮學生的創造性思維，燃起學生的創新火花，讓“意外”演繹精彩生成.

案例4 如圖7所示，已知正方形ABCD的邊長為4，現沿著EF折疊并使點B與邊AD上的點M重合，點C位于點N處，且MN、CD相交于點P，連結EP.

（1）如圖8，若點M為邊AD的中點時，①△AEM的周長為_________;②證明：EP=AE+DP.

（2）當M為邊AD上一動點時（M不落于點A、D處），△PDM的周長是否變化？請闡明理由.

學生在解決第（1）題的②時，很快聯系到梯形的中位線進行解答.

師：能想到其他方法來證明嗎？

生1：延長EM、PD，相交于點G，證明△AEM≌△DGM，后求證EP=PG.

師：很好. 還有其他方法嗎？

生2：我認為可以先利用勾股定理算出三條邊，然后即可證明.

（筆者也未曾想到代數方法在這一問題的解決中的合理運用. 經過生2的提醒，結合再度思考后發現這樣一來“邊長為4”這一條件也得到巧妙運用.）

生2：直角三角形AEM中，設AE=x，根據勾股定理得出x= . 因為△AEM∽△DMP，可得DP= . 作EH⊥DP，直角△EHP中，EH=4，PH= - = . 再根據勾股定理可得EP= ，得證.

師：說得太好了！這一方法巧妙地將幾何問題轉化為代數問題來解決，很不錯！

上述案例中由于教師的追問有效激發了學生對于“轉化”策略的需求，進一步使他們的思維被激活. 通過生2的精彩解說學生們思路打開了. 在問題（2）的解決中也生成了多種精彩解法，促進了具有價值的思維經驗的生長.

綜上所述，課堂追問是當前課程改革中的一大亮點，只有把握好追問的時機，科學合理地追問，才能有效發揮教學價值，發展學生的數學素養 .[2]

參考文獻：

[1] 溫建紅. 論數學課堂預設提問的策略[J]. 數學教育學報，2011，20（3）.

[2] 張奠宙，張蔭南. 新概念：用問題驅動的數學教學[J]. 高等數學研究，2004（5）.