二輪復習要引導學生抓解題“特征”

廣東 陳躍琳

新一輪的課程改革已經進入關鍵時期，在教育教學中越來越強調培養學生的數學核心素養和學習能力.近年來，高考制度的改革給高考復習備考帶來了深刻的變革，在復習中教師越來越注重學習方法、解題方法的傳授，而不只是向學生傳授基礎的學科知識.數學是促進學生能力發展、思維提高以及認知水平提高的基礎性學科.但是由于高中數學知識的復雜性、抽象性使很多學生在學習過程中望而生畏.二輪復習是提升學生能力的階段，若教師在數學解題教學中的教學方式以及教學理念運用不當，就會使得學生的復習效率低下，表面上看，每天都沉浸在高壓的學習中，但是并沒有什么太大的效果.因此，教師必須要轉變教學理念和教學方式，引導學生對不同類型題目的特征進行總結和歸納，掌握不同的解題方法，讓學生在做題過程中體會數學的魅力.

許多數學問題，細心觀察就會發現，無論是條件、結論，還是數值、結構形式等，都表現出或隱含著某些“特征”，這些“特征”是問題的“題眼”，是解決問題的切入點.在二輪復習教學中，教師要善于引導學生抓住這些“特征”，并以這些“特征”為導向進行分析、變換、聯想、構造，這樣可以快速獲得解決問題的思路或優化解決問題的過程.下面從幾方面闡述抓“特征”在數學解題中的導向作用.

一、數據特征

許多數學問題，都會出現具有某種特征的數據，會對問題的解決起著導向作用.只要注意觀察、分析，重視挖掘，從數值本身的變化、數值與數值之間的聯系去尋找解題的切入點.

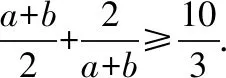
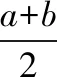
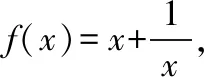
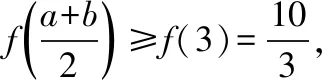
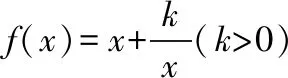
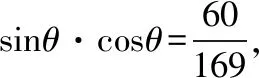
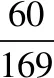
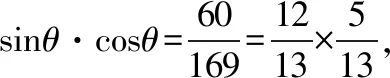
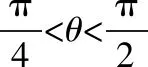
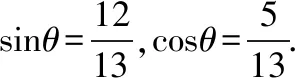
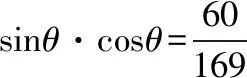
二、位置特征

與圖形(象)有關的一些數學問題都有它特定的位置關系，若能細致分析某些關鍵的點或線的位置“特征”，不僅可以簡化運算過程，甚至可以得到不攻自破的解題效果.

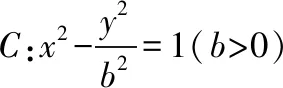
解析：雙曲線C的一條漸近線平分圓的周長，意味著這條漸近線經過圓的“圓心”.抓住這一位置關系，問題便容易攻破.

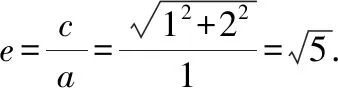
點評：若不能發現雙曲線C的漸近線經過圓的“圓心”這一位置關系，則很難處理漸近線將圓的周長平分，也就無法順利解決問題.

例4.(2018·全國卷Ⅲ·理6文8)直線x+y+2=0分別與x軸，y軸交于A，B兩點，點P在圓(x-2)2+y2=2上，則△ABP面積的取值范圍是

( )

A.[2，6] B.[4，8]

解析：由于|AB|是確定的，所以△ABP面積的取值范圍取決于點P到直線x+y+2=0的距離.所以過圓心作直線x+y+2=0的垂線，與圓的交點即為所求的點P的位置.

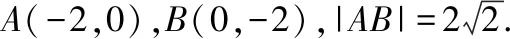
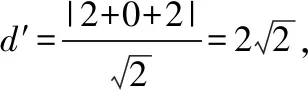
點評：發現“過圓心作直線x+y+2=0的垂線，與圓的交點即為所求的點P的位置”是順利解決問題的關鍵.

三、圖形特征

有些抽象的數量關系，若轉化為具體的圖形問題，并抓住圖形特征，則思路直觀、清晰，有利于快速解題.

例5.(2017·全國卷Ⅰ·理13)已知向量a，b的夾角為60°，|a|=2，|b|=1，則|a+2b|=________.

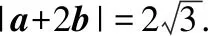
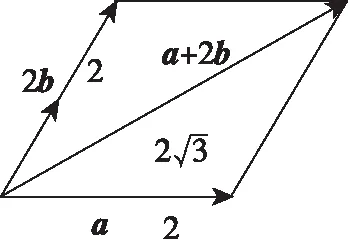
點評：向量具備代數和幾何特征，在處理涉及向量模的一類問題時，若充分運用“圖形特征”會加快解題速度，可使問題得以“秒殺”.

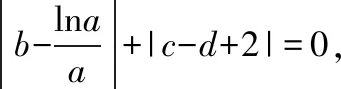
解析：由(a-c)2+(b-d)2很容易聯想到它的幾何意義，其表示兩點(a,b),(c,d)的距離的平方.

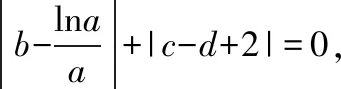
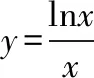
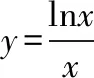
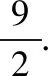
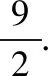
點評：有些多元問題表面上看起來比較繁瑣，無從下手，而轉換視角，挖掘題設條件中蘊含的圖形特征，便可找到問題解決的切入點.比如本題就是將代數問題幾何化，并借助導數來分析動點間的距離問題，對培養學生的數學抽象這一核心素養有一定的幫助.

四、結構特征

數學問題條件或結論中的數、式結構常常隱含著某種特殊的關系，注意洞察并加以分析、加工和轉化，可迅速找到解決問題的思路.

例7.設x、y為實數，且滿足

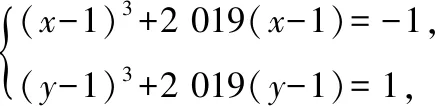
解析：條件中兩方程左邊的結構形式相同，為此，構造函數f(x)=x3+2 019x，并討論其單調性和奇偶性從而達到解題的目的.

構造函數f(x)=x3+2 019x，易知它是奇函數，且在R上單調遞增.

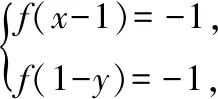
所以x-1=1-y，即x+y=2.

點評：若按常規方法求解此題，難度較大，甚至無法入手.這里通過構造函數，利用函數的奇偶性和單調性轉化求解，方法巧妙，且過程簡潔.

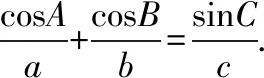
(Ⅰ)證明：sinAsinB=sinC；

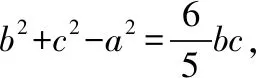
解析：(Ⅰ)略.

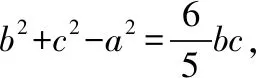
因為A為△ABC的內角，所以A∈(0,π)，sinA>0，

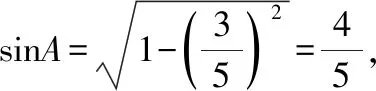
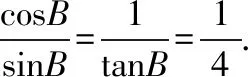
所以tanB=4.

五、差異特征

許多數學問題的條件與結論之間、“量”與“量”之間，往往表現出一些“差異”關系，這些“差異”以特有的方式直接或間接地暗示著解題的方向.

例9.已知函數f(x)=ax-bx(a>0,a≠1).

(Ⅰ)若函數y=f(x)在點(1,f(1))處的切線方程為y=(e-1)x，求函數f(x)的解析式；

(Ⅱ)在(Ⅰ)的條件下，設g(x)=x2-x+m，若?x0∈R，使?x∈R不等式f(x)>g(x0)成立，求實數m的取值范圍.

解析：(Ⅰ)因為f(x)=ax-bx(a>0,a≠1),所以f(1)=a-b=e-1.

又因為f′(1)=alna-b=e-1，所以a=e，b=1，所以f(x)=ex-x.

(Ⅱ)x0是存在量，x是任意量，從這一“差異”中我們可以意識到問題需要轉化求解才能奏效.

?x0∈R，使?x∈R不等式f(x)>g(x0)成立?當x∈R時，f(x)min>g(x)min.

當x≥0時，f′(x)=ex-1≥0，所以f(x)在區間[0,+∞)上單調遞增.

當x<0時，f′(x)=ex-1<0，所以f(x)在區間(-∞,0)上單調遞減.

所以函數f(x)在(-∞,+∞)上的最小值為f(0)=1.

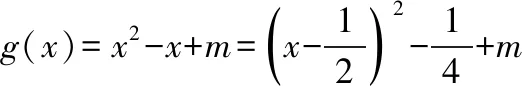
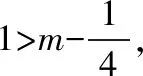
點評：數學中的“任意量”與“存在量”常見常用，變式多樣，內涵深刻.本題依據“量”與“量”之間的差異，將條件不等式的成立等價轉化為函數的最值關系求解，體現了化歸與轉化思想的應用.

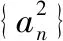
解析：條件中給出了兩個“不等量”關系，結論探求的是“等量”關系.通過對這一差異“點”的分析，獲知解題的切入點就是化“不等”為“等”.

因為Sn≤n2+n-1，所以S1=a1≤12+1-1=1，即a1≤1.①

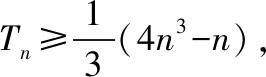
由①②得a1=1.

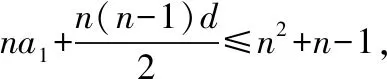
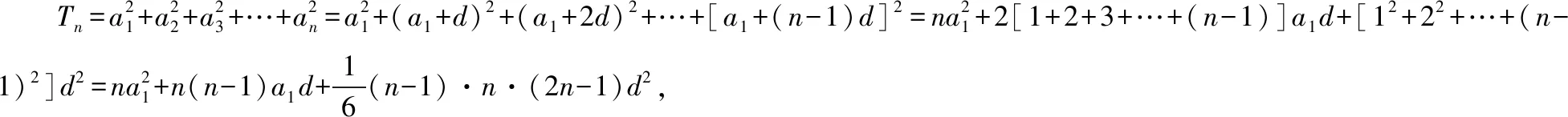
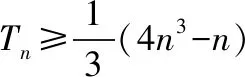
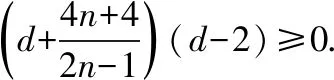
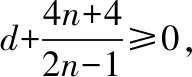
故由③④可得d=2.

點評：本題通過對“等”與“不等”的差異“點”的分析轉化，使得不等式中的“夾逼”法則：“如果實數x,a滿足a≤x≤a(即x≥a且x≤a)，則必有x=a”在本題求解中起了重要的作用.