高三數學復習教與學如何練內功
浙江 余繼光
高考面對的是新穎的數學問題,應試者必須把握其本質,采取有效方法積極應對,而這種應對能力必須通過復習教學練“內功”來達到.教學中不僅要有明白算理的解答題求解的思維訓練,而且還要增加凸顯數學問題本質的快速求解思維的訓練.
一、挖掘亮點,尋找復習著力點
【亮點一】以抽象符號檢測學生理解數學本質
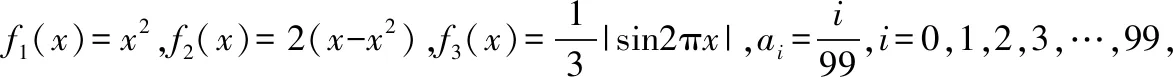
( )
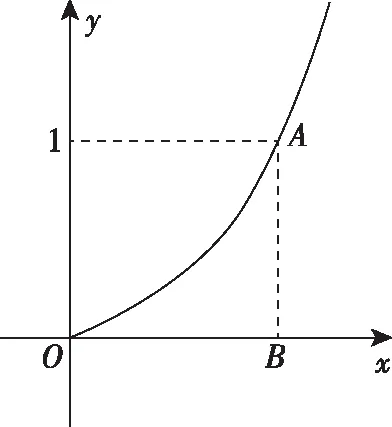
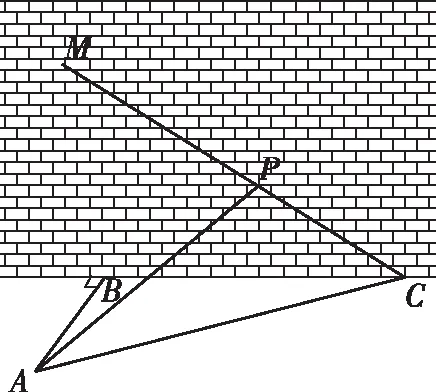
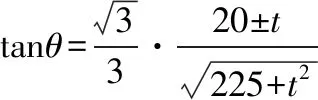
A.I1 C.I1 解法一:f1(x)在[0,1]上單調遞增,所以|f1(ai+1)-f1(ai)|=f1(ai+1)-f1(ai), I1=f1(a1)-f1(a0)+…+f1(a99)-f1(a98)=f1(a99)-f1(a0)=f1(1)-f1(0)=1, 所以當i≤49時,|f2(ai+1)-f2(ai)|=f2(ai+1)-f2(ai); 當i≥50時,|f2(ai+1)-f2(ai)|=-[f2(ai+1)-f2(ai)], I2=f2(a1)-f2(a0)+…+f2(a50)-f2(a49)+f2(a50)-f2(a51)+…+f2(a98)-f2(a99)=2f2(a50)-f2(a0)-f2(a99)<1, 當25≤i≤49和i≥75時,|f3(ai+1)-f3(ai)|=-[f3(ai+1)-f3(ai)]; 且f3(a24) 解法二: 圖1 圖2 圖3 應試者不能采用解法一,教學中,教師介紹解法一的目的是讓學生理解解法二的思想,而這種思想,不僅在小學數學學習中已經接觸過,而且在未來高等數學的學習中也是非常有用的. 【亮點二】以思維的多樣性檢測學生的創新能力 例2.已知甲盒子中僅有1個球且為紅球,乙盒子中有m個紅球和n個藍球(m≥3,n≥3),從乙盒子中隨機抽取i(i=1,2)個球放入甲盒子中. (1)放入i個球后,甲盒子中含有紅球的個數記為ξi(i=1,2); (2)放入i個球后,從甲盒子中取1個球是紅球的概率記為Pi(i=1,2),則 ( ) A.P1>P2,Eξ1 B.P1 C.P1>P2,Eξ1>Eξ2 D.P1 解法二:特殊化思想.取m=3,n=3,則 解法三:模型化思想,將古典概型問題轉化為溶液的濃度問題. 將紅球理解為純紅色的溶液,藍球理解為純藍色的溶液,如果一個盒子中有兩種顏色的球,理解為兩種溶液的混合,把概率理解為濃度,期望理解為溶質的含量. 乙盒子中紅色溶液的濃度不是100%,所以從乙盒子中取一個單位的溶液倒入甲盒子中,甲盒子中紅色溶液的濃度肯定會降低,所以有P1>P2,但甲盒子中紅色溶液的溶質肯定會增加,因此,Eξ2>Eξ1.下面用溶液計算方法也可以證明. ②從乙盒子中兩次各取一個單位的溶液倒入甲盒子后, 解讀:表面上是一個復雜的問題,但采用特殊化思想可以迅速求解,如果能達到模型化思想水平,也可以迅速求解.解法一適合于平時的算理教學,此題的設計給中學教師的啟示是如何把大問題化成快速求解的小問題. 【亮點三】以數學應用問題檢測學生的實踐能力 例3.如圖,某人在垂直于水平地面ABC的墻面前的點A處進行射擊訓練.已知點A到墻面的距離為AB,某目標點P沿墻面的射線CM移動,此人為了瞄準目標點P,需計算由點A觀察點P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,則tanθ的最大值為________(仰角θ為直線AP與平面ABC所成角). 解法二:由解法一可見,問題化歸為函數 用判別式法也可以求解: u2(225+t2)=400±40t+t2,即(u2-1)t2±40t+225u2-400=0, 用三角換元法也可以求解: 解法三:過點P作PD⊥BC,且AB⊥BC,AB=15,AC=25, 1.學生數學訓練必須練“內功” 學生說2014年高考數學理科試卷難,難在哪兒?做過一遍后,發現試卷涉及絕對值函數、無理函數、最優化等問題較多,涉及不等式的求解與轉化等運算較多,特別是字母運算或代數變形;面對新穎的數學問題,學生運用數學思想的意識不到位,結果費時費力且無效;面對復雜的數學問題,學生不能迅速識別其數學模型,腦海中數學模型少,轉化能力弱,應試心理慌,最后以“難”以突破而告終! (1)在運算能力上練“內功” 在高考不允許使用計算器的年代,首先,在計算能力上必須過關,事實上,由于初中允許使用計算器,使學生到高中后的計算能力大打折扣,數字的四則運算都會經常錯,因此平時要心算、筆算一起練;其次,代數式的因式分解、多項式的綜合除法、方程的解法、不等式的解法等在按照規則步驟運算的同時,需注意運算方向的優化,教師要在各輪復習教學中有意識地設計運算能力提升的小練習. (2)在思想方法上練“內功” 七大數學思想(函數與方程、數形結合、分類與整合、化歸與轉化、特殊與一般、有限與無限、統計與概率)與七小具體方法(歸納推理、類比推理、演繹推理、綜合法、分析法、反證法、歸納法)是高考數學命題檢測的核心,尤其是在面對同一個數學問題,采取不同的語言表達方式(自然語言、符號語言、圖形語言等)設計時,用數學思想與方法理解其本質是應試關鍵,這也是浙江高考數學命題的一大特色.如上述例1與例2. (3)在數學模型上練“內功” 數學模型是數學問題的核心,掌握更多的數學模型及解決模型的方法,在應試時就會比較坦然,正如在社會生活中一樣,準備的工具、技能、方法多,識別的模型多,解決問題的能力就較強,無論是代數中的數列,三角中的變換,幾何中的圖形,還是概率統計中的計數,解析幾何中的曲線,都有經典的數學模型,把握了數學模型,就可舉一反三,如上述例3中的經典數學模型. 2.教師數學復習凸顯練“內功” 為了提升學生的“內功”水平,教師必須首先具有三大“內功”:會解題,準精簡,化變拓. (1)在“會解題”上練“內功” 數學解題能力是一個教師的立身之本,每位數學教師都要成為數學解題高手,在高三復習中,經過至少兩個輪回的解題訓練,才能達到數學解題的基本要求. 第一輪達到第一層次:面對各種各樣的數學題要會解,尋找到問題的答案; 第二輪達到第二層次:不僅會尋找問題的答案,而且要能說出為什么這樣解; 第三輪達到第三層次:能夠說出最優解或數學模型并能引申到更一般的情形. (2)在“準精簡”中練“內功” 在數學復習的題海教學中,教師最容易導致“三不”,即不準——數學概念不能準確把握、不精——個人精力達不到對數學概念與知識的實質性理解、不簡——常常把簡單的數學問題講復雜了,因此,高三教師數學復習必須做到以下三點: 一是數學概念準確到位.比如,關于函數零點、極值點等的表述,學生常表達出錯,將其理解為二維的平面點,而它們實際上是“代數點(一維點)”.教師對每一個核心概念、關鍵的知識點都要講到位,講準確. 二是講解思想精力充沛.比如,高三數學講題往往就題論題給出答案,不能把題目串起來,講思想方法與數學模型能使學生舉一反三,統領全局.教師可以通過一題多變、一題多解、多題一解、多題一型等,把思想方法歸納總結,使學生腦中的知識編成網絡狀. 三是復雜問題簡單淺出.比如,高三數學中有簡單問題,教師可能會講得很復雜,而復雜問題講得更復雜,這樣容易使學生產生畏難情緒,失去解題的動力與激情;教師若能把復雜問題講得簡單才能顯示出教師教學的功底. (3)在“化變拓”中練“內功” 在數學復習教學中,教師常采取的教學方法是把高考題或模擬題整題照搬來講,這樣往往會沖淡主題,使學生不能集中精力掌握重點,只能達到事倍功半之效,因此,高三數學復習最好的方法有以下三種: 一是化大為小.為了講某一個知識點,把一個“大”的問題化成“小”問題,如高考數學解答題一般都有幾問,可以將其拆成小問題來講;也可以把若干個“大”問題中的“小”問題串成一起,來集中講一個專題,形成一個數學模型,把握一個突破口. 二是變式教學.“變式”思想是中國基礎教育的精髓,也是提升學生理解力的有力武器.如果一個數學問題在教師手中達到“順水推舟、順手牽羊、順藤摸瓜”式的變化程度,使學生達到“能學、善學、樂學”的境界,師生的“內功”都將達到一個較高水平.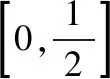

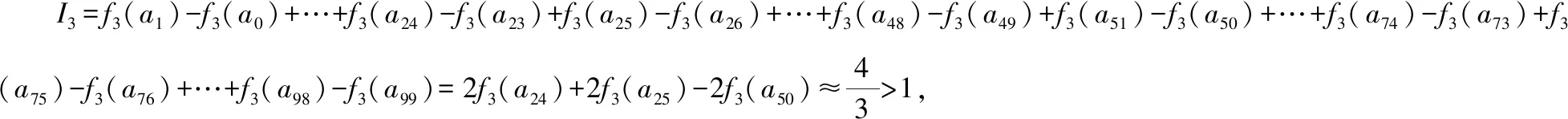
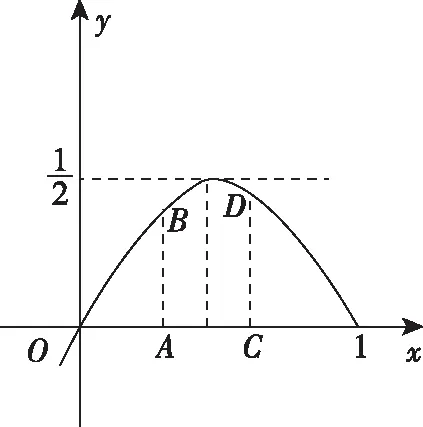
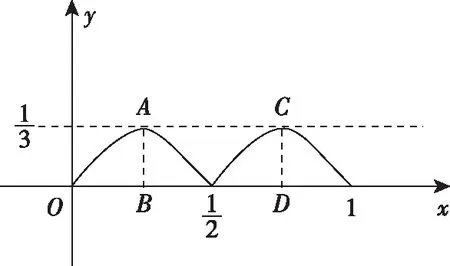
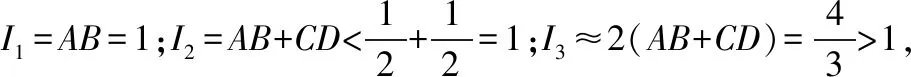
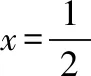
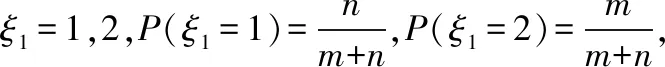
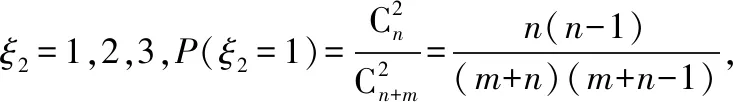
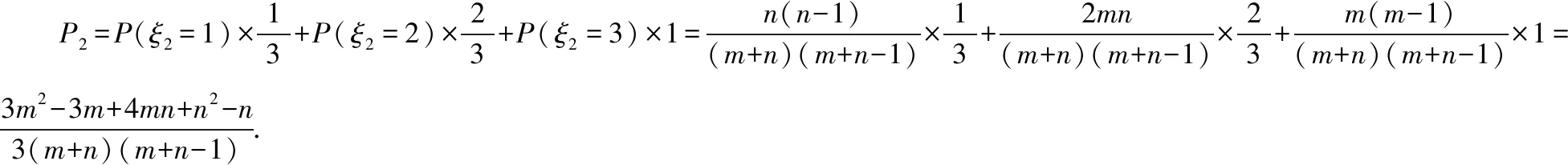
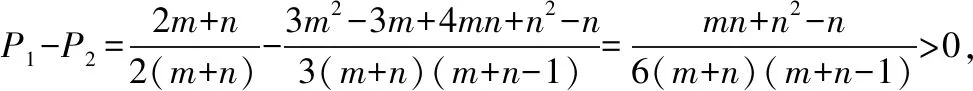
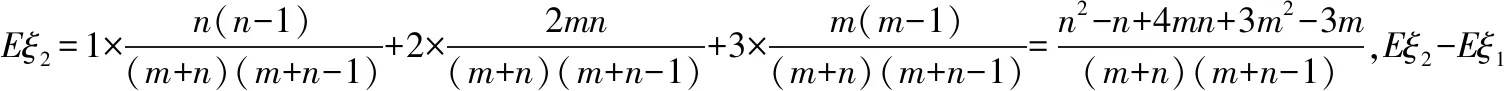
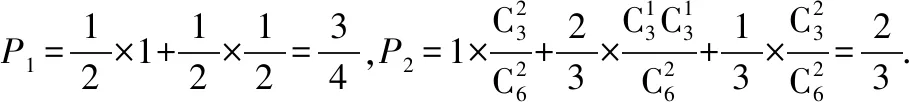
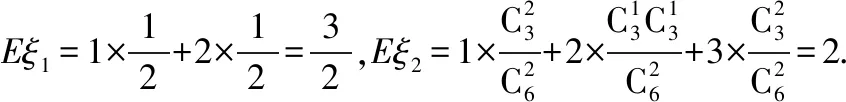
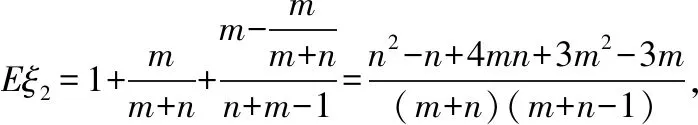
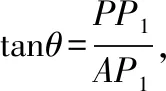
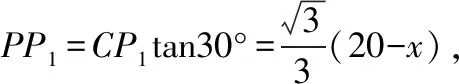
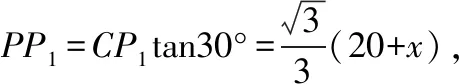
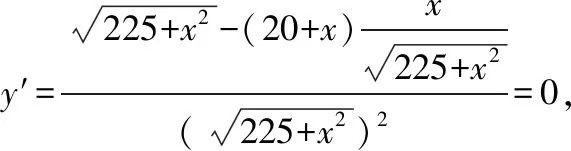
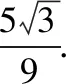
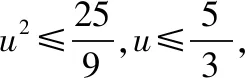
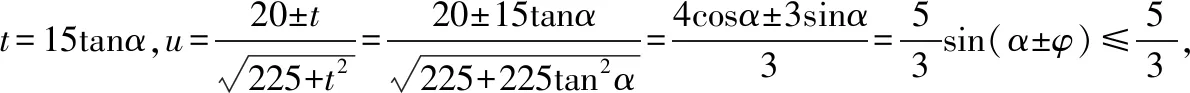
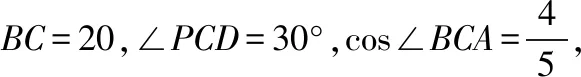
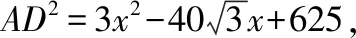
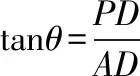
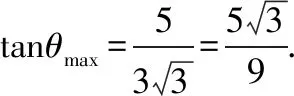
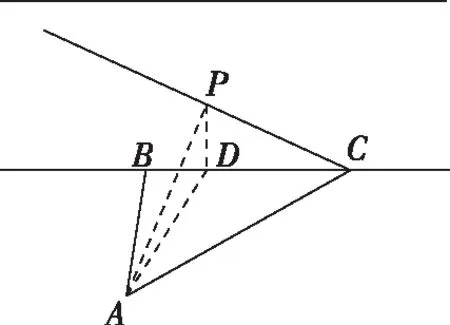
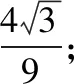
二、苦練內功,提升復習有效性


