基于深度教學的高三復習課教學案例

廣東 王常斌

在高三的復習中，我們經常會涉及選題和編題，高考試題是我們首選材料.選題和編題看似一件小事，但其中大有學問.多數教師選題是文科班從文科卷中選題，理科班從理科卷中選題，覺得題好就選，但并未將這些題歸類，而是將題一道道孤立起來，課堂上也只是就題講題，這樣導致的結果是學生所學到的知識是零碎的，很難形成系統，從而學生的思維能力很難得到應有的提升.下面以一節高三解析幾何的復習課的選題及課內的處理為例，來談談如何在課堂中進行深度教學.

【課例】直線與圓錐曲線相交所成的等角問題.

2018年全國卷Ⅰ中的解析幾何題，老師們都覺得較好，雖然不像以前難度那么大，但對學生的運算求解、直觀想象、邏輯思維以及解析幾何的基本思想和解題策略都有較好的考查，題目如下：

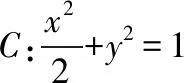
(Ⅰ)當l與x軸垂直時，求直線AM的方程；

(Ⅱ)設O為坐標原點，證明：∠OMA=∠OMB.

題2(2018·全國卷Ⅰ·文20)設拋物線C：y2=2x，點A(2，0)，B(-2，0)，過點A的直線l與C交于M，N兩點.

(Ⅰ)當l與x軸垂直時，求直線BM的方程；

(Ⅱ)證明：∠ABM=∠ABN.

對于高三教師，想選擇上面的試題，是文科班選文科題，理科班選理科題，還是都選？在課內應如何處理？下面談談筆者的看法.

這兩道題顯然是姊妹題，所考查的知識內容、設問方式、對考生的能力要求及解決問題的方法基本一致，所不同的是理科試題(題1)以橢圓為載體，文科試題(題2)以拋物線為載體進行考查.所以我認為不管是文科班還是理科班，這兩道題一定要同時選，并且還要增加一道題：

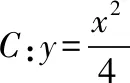
(Ⅰ)當k=0時，分別求C在點M和N處的切線方程；

(Ⅱ)y軸上是否存在點P，使得當k變動時，總有∠OPM=∠OPN？請說明理由.

我們還要選上面的題3是因為這三道題屬于同一類題，我們要歸類進行講解.顯然題2與題3更為接近，所以這三道題我們可以先處理題2或題3.

【課內講解建議】

題2和題3誰先誰后呢？這得看學生的基礎.如果學生基礎特別好，可以從題3入手，如果學生基礎薄弱，可以從題2入手.如果按照由易到難，由特殊到一般的話，我們還是建議從題2開始入手.

題2并不難，可讓學生獨立探索加以解決，當然，如果學生碰到困難，教師可以在恰當的時候進行點撥和提示，如將證明角相等問題轉化為兩直線的斜率互為相反數問題、韋達定理的應用等.

題2做完后，我們可以讓學生做題3，題3有一定的難度，教師應在教學過程中給予應有的提示和幫助.

附：題3第(Ⅱ)問的解答：

(Ⅱ)解：假設在y軸上存在點P(0,t)，使得當k變動時，總有∠OPM=∠OPN.

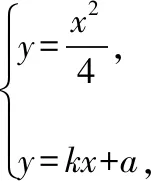
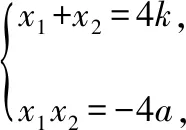
由∠OPM=∠OPN得kPM=-kPN，即kPM+kPN=0，

所以x2(y1-t)+x1(y2-t)=0，

又x2(y1-t)+x1(y2-t)=x2(kx1+a-t)+x1(kx2+a-t)=2kx1x2+(a-t)(x1+x2)=-8ak+4(a-t)k=0，

所以a+t=0，故t=-a，

因此存在點P(0,-a)，使得當k變動時，總有∠OPM=∠OPN.

【總結】兩題做完后，教師一定要及時讓學生進行總結，可設計以下問題：

1.題2與題3有哪些相似之處？有哪些不同之處？

2.題3可以推廣到一般的情況嗎？

設計這兩個問題是為了讓學生經歷由特殊到一般的猜想，培養學生的數學抽象素養.

問題1較容易，學生能獨立解答：

(1)均是以拋物線為載體進行考查，均考查直線與拋物線的位置關系；

(2)第(Ⅰ)問均是直線與拋物線的對稱軸垂直時求滿足條件的直線方程；

(3)第(Ⅱ)問要解決的問題相同，都要求證明兩角相等，即∠OPM=∠OPN，∠ABM=∠ABN；

(4)解決問題的方法一樣.第(Ⅱ)問中的兩角相等的條件均轉化為兩直線斜率和為零.

不同的是第(Ⅱ)問設問的方式，題3是探索性問題，而題2是證明題，相較之下題3更具一般性.

對于問題2，如果學生不能獨立解決，可讓學生討論得出結論.

猜想1：對于任意x2=2py，其對稱軸上關于拋物線頂點對稱的任意兩點A(0,a),B(0,-a)(設a與p同號)，過點A的任意直線與拋物線相交于M,N兩點，則總有∠OBM=∠OBN(或∠ABM=∠ABN).

事實上，猜想1完全正確，證明過程與上述例題相仿，留給讀者自行證明.

猜想1中，拋物線的對稱軸是y軸，當對稱軸換成x軸，結論一樣成立，即如下推論.

推論1：對于任意y2=2px，其對稱軸上關于拋物線頂點對稱的任意兩點A(a，0),B(-a，0)(設a與p同號)，過點A的任意直線與拋物線相交于M,N兩點，則總有∠ABM=∠ABN.

在推論1中，令p=1，a=2，不就是2018年全國卷Ⅰ的文科試題(即題2)嗎？由此可以看出，題2完全是由題3變化而來的，題2只是題3的特例而已！這就可以理解為什么題3比題2難，題3為理科題，題2為文科題.

做完題2與題3并且歸納得出一般性的結論后，就可以讓學生做題1了，很顯然理科試題(題1)是在文科試題(題2)的基礎上改編的.研究的問題一樣，設問的方式一樣，唯一不同的是將曲線換了，由拋物線換成了橢圓.題1的解題思路與方法和題2完全一樣，解答過程基本類似，學生不難完成.

我們的教學是否到此為止呢？如果這樣，學生就失去了一個提升思維的極好的機會.做完題1，教師一定要設計問題讓學生思考：

由題2和題3，我們得出了關于拋物線的一般結論(猜想1)，類似地，題1可以推廣嗎？即對橢圓有類似的結論嗎？

先讓學生獨立思考，如果想不出，可以小組討論，必要時教師啟發.

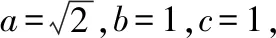
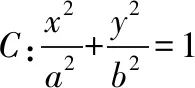
我們來證明猜想2.

證明：當直線l與x軸重合時，顯然∠OMA=∠OMB=0°.

當直線l與x軸不重合時，可設l的方程為x=ty+c，

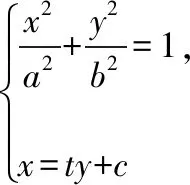
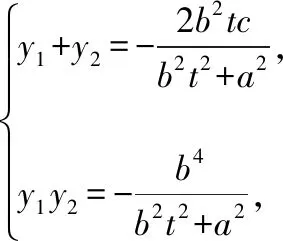
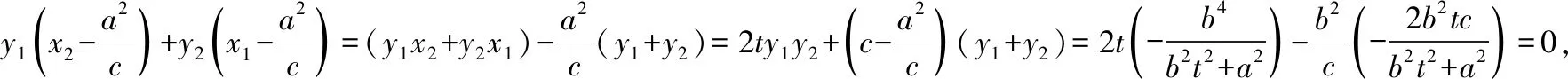
所以有kMA+kMB=0，即kMA=-kMB，

故∠OMA=∠OMB.

三道題都完成了，并且推廣到了一般的結論，是否可以止步了呢？其實課上到這里，教師不提問，學生也會問：圓錐曲線是一個整體，它包含拋物線、橢圓和雙曲線，既然拋物線、橢圓有這樣的性質，那么雙曲線呢？類似地，我們可以得到：

上面的猜想3也完全正確，讀者可以自行證明.

至此，直線與圓錐曲線相交所成的等角問題就完整了，但為了課堂的進一步延伸，我們可以提出以下問題讓學生思考：

1.上面關于橢圓與雙曲線的猜想中，直線經過其焦點，點M正好是準線與長軸所在直線的交點.如果直線不經過焦點，還有沒有類似的結論呢？如果有，點M的坐標又是什么呢？

2.圓錐曲線其實有統一的定義，那么我們今天的三個猜想能否用統一的形式來表達呢？

這兩個問題可以留給學生課后進行研究性學習.