跨越運算“門檻”，提高運算素養

安徽 朱啟州

高中教師常常抱怨學生運算能力不足，學生常因運算失誤造成“會而不對”，結果后悔不已，運算“門檻”制約學生數學素養的發展.我們知道，數學運算是數學演繹推理的重要方法，是解決數學問題的基本途徑.學生通過理解運算對象、掌握運算法則，通過算法的探求與選擇，培養學生數學思維能力與分析問題解決問題能力，培養學生嚴謹求實的理性思維品質.現就如何在高中數學復習教學中，提高學生運算素養談幾點看法，供讀者參考，不足之處，請批評指正.

一、重視算法、多路探求與選擇是跨越運算“門檻”的重要方法

【例1】(2017·上海卷·15)已知a，b，c為實常數，數列{xn}的通項xn=an2+bn+c，n∈N*，則“存在k∈N*，使得x100+k，x200+k，x300+k成等差數列”的一個必要條件是

( ).

A.a≥0 B.b≤0

C.c=0 D.a-2b+c=0

【分析】本題試圖通過特殊值法進行篩選不容易得出結果，故選用綜合法.將條件“x100+k，x200+k，x300+k成等差數列”轉化為2x200+k=x100+k+x300+k，進而2[a(200+k)2+b(200+k)+c]=a(100+k)2+b(100+k)+c+a(300+k)2+b(300+k)+c，若直接進行計算就有點煩瑣，可令t=200+k，于是上式轉化為2at2+2bt+2c=a(t-100)2+b(t-100)+c+a(t+100)2+b(t+100)+c，很容易得到20000a=0，即a=0，故選A.

【點評】在上述解題中，顯然綜合法運算環節少、較簡單，表現為通過同一問題的不同運算途徑的多路探求，篩選出更簡捷的方法.這就要求我們在復習課的教學中引導學生利用多種途徑探尋解題，注意算法的優選，增加運算的思維含量，養成且思且算的良好習慣.

二、善于從全局角度思考是跨越運算“門檻”的重要途徑

( )

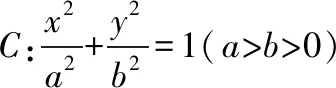
三、善于等價轉化問題中的關鍵信息是跨越運算“門檻”的法寶

【分析】在一個數學問題中，最復雜的那個條件往往是核心條件，將這樣的條件化為易于理解和運用的條件，達到“撥云驅霧”的目的.本題第二個條件較復雜，宜對其進行整理化簡.

四、適當地精熟化訓練是跨越運算“門檻”的基本功

【例4】(2018·全國卷Ⅰ·理16)已知函數f(x)=2sinx+sin2x，則f(x)的最小值是________.

【點評】本題為函數的最值問題，研究函數的單調性是最基本最重要的方法，而導函數法又是最有效的方法.在求導過程中，不少學生因對復合函數求導不熟練，常犯(sin2x)′=cos2x的錯誤，對本題來說，學生熟練求函數的導函數就顯得關鍵了.俗話說“熟能生巧”，我們不主張過度訓練，但是對運算法則、運算技能進行適當地精熟化訓練也是必需的，是運算能力形成的不可或缺的過程，是培養學生“數學運算核心素養”的基本要求.因此，平時教學中數學解題訓練要落到實處，要給學生留出一定的獨立運算實踐的時間與空間.

五、養成良好的運算習慣是跨越運算“門檻”的根本

【解析】由an+1-an=2n，得an-an-1=2(n-1)(n≥2,n∈N*)，

所以a2-a1=2×1，a3-a2=2×2，…，an-an-1=2(n-1)，

所以an=n2-n+33，