巧借結論妙解題，奇思妙想三角形

江蘇 韓文美

三角形的三邊長與面積之間存在很多富有創意的關系.下面通過證明給出一個三角形的三邊長的線性平方和與面積之間存在的不等式，并利用該不等式進一步變式拓展，得到一些相關的推論，同時利用該不等式來解決一些與之相關的最值問題.利用該不等式來處理，可使得問題的解決變得更為簡單快捷.

1.結論呈現

點評：通過余弦定理加以轉化，結合關系式的配湊并利用基本不等式來處理，巧妙引入三角函數的平方關系，利用柯西不等式以及三角形的面積公式來加以轉化與應用，進而得以證明涉及三角形的三邊長的線性平方和、三角形的面積以及相關參數之間的不等式成立.

2.拓展推論

分析：結合條件確定對應系數值x=y=z=1，結合以上不等式結論，代入即可確定三角形的三邊長的平方和與面積之間存在的不等式結論.

證明：由題知x=y=z=1，

利用以上不等式結論可得

分析：結合條件確定三角形的三邊長的線性平方和ma2+nb2+tc2=k為已知值，結合以上不等式結論，代入即可確定涉及三角形的面積的最大值.

證明：由于ma2+nb2+tc2=k，

分析：結合條件確定對應系數值x=a，y=b，z=c，結合以上不等式結論，代入即可確定三角形的三邊長的高次代數式與面積之間存在的不等式結論.

證明：由題知x=a，y=b，z=c，

分析：結合條件確定對應系數值x=b，y=c，z=a，結合以上不等式結論，代入即可確定三角形的三邊長的高次代數式與面積之間存在的不等式結論.

證明：由題知x=b，y=c，z=a，

利用以上不等式結論可得

3.實際應用

3.1三角形的三邊長的線性平方和的最值問題

例1.(河南省天一大聯考2018-2019學年高中畢業班階段測試(二))在面積為2的△ABC中，a，b，c分別為內角A，B，C的對邊，則a2+2b2+c2的最小值為________.

分析：結合條件確定三角形的面積值以及對應系數值x=1，y=2，z=1，結合以上不等式結論，代入即可確定涉及三角形的三邊長的線性平方和的最小值.

解析：由題知S=2，x=1，y=2，z=1，

利用以上不等式結論可得

點評：利用以上不等式結論來處理此類涉及三角形的三邊長的線性平方和的最值問題，解決問題易操作，目標明確，處理過程簡單易懂.而采取其他相關方法來處理，過程較為繁瑣，難度也比較大.

3.2三角形的面積的最值問題

例2.(2018年浙江省名校協作體試題)在△ABC中，內角A，B，C所對的邊分別為a，b，c，若2a2+b2+c2=4，則△ABC面積的最大值為________.

分析：結合條件確定對應系數值x=2，y=1，z=1，結合以上不等式結論，代入即可確定涉及三角形的面積的最大值.

解析：由題知x=2，y=1，z=1，

利用以上不等式結論可得

點評：利用以上不等式結論來處理此類涉及三角形的面積的最值問題，關鍵是結合題目條件，與以上不等式結論加以聯系，這樣易于操作，方便求解.而采取其他相關方法，如何將涉及三角形的三邊長的線性平方和向三角形的面積轉化，難度比較大，比較難破解.

3.3三角形的三邊長的高次代數式的最值問題

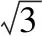
分析：結合條件確定三角形的面積值以及對應系數值x=a，y=b，z=c，結合以上不等式結論，代入即可確定涉及三角形的三邊長的高次代數式的最小值.

解析：由題知x=a，y=b，z=c，

利用以上不等式結論可得

所以a3+b3+c3的最小值為24.

點評：直接來分析與求解，無法下手，又涉及三角形的三邊長的高次代數式a3+b3+c3，沒有較好的轉化與化歸思維.而利用以上不等式結論來處理此類涉及三角形的三邊長的高次代數式的最值問題，巧妙地把對應的系數轉化為特殊的邊長問題，一般中含有特殊，可以非常有效地轉化問題，進而達到解決問題的目的.

3.4三角形的三邊長的其他代數式的最值問題

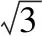
利用以上不等式結論可得

點評：破解本題是否可用其他方法來處理，大家可以嘗試一下.而利用以上不等式結論來處理此類涉及三角形的三邊長的其他代數式的最值問題，也是巧妙地把對應的系數轉化為特殊的邊長問題，此時以除法形式出現，更具一般性，而具體解答時只要加以正確轉化，就可以簡單快捷地處理問題，達到解決問題的目的.