數學探究 樂在其中

江蘇省如皋中學高二(1)班 (郵編：226500)

江蘇省如皋中學 指導老師 范棟志 (郵編：226500)

筆者對2018年南通市高三第二次調研試題第13題有關向量數量積的問題進行了深度探究.從最初的思考起步，扣住關鍵，不斷優化，自我設問，大膽嘗試，逐層深入.在探究的過程中不斷完善知識網絡體系，更深層次地認識到基礎知識、基本方法、基本能力在解題中的重要作用.在探究的過程中有煩惱，更有樂趣，并樂在其中.

圖1

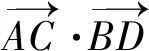
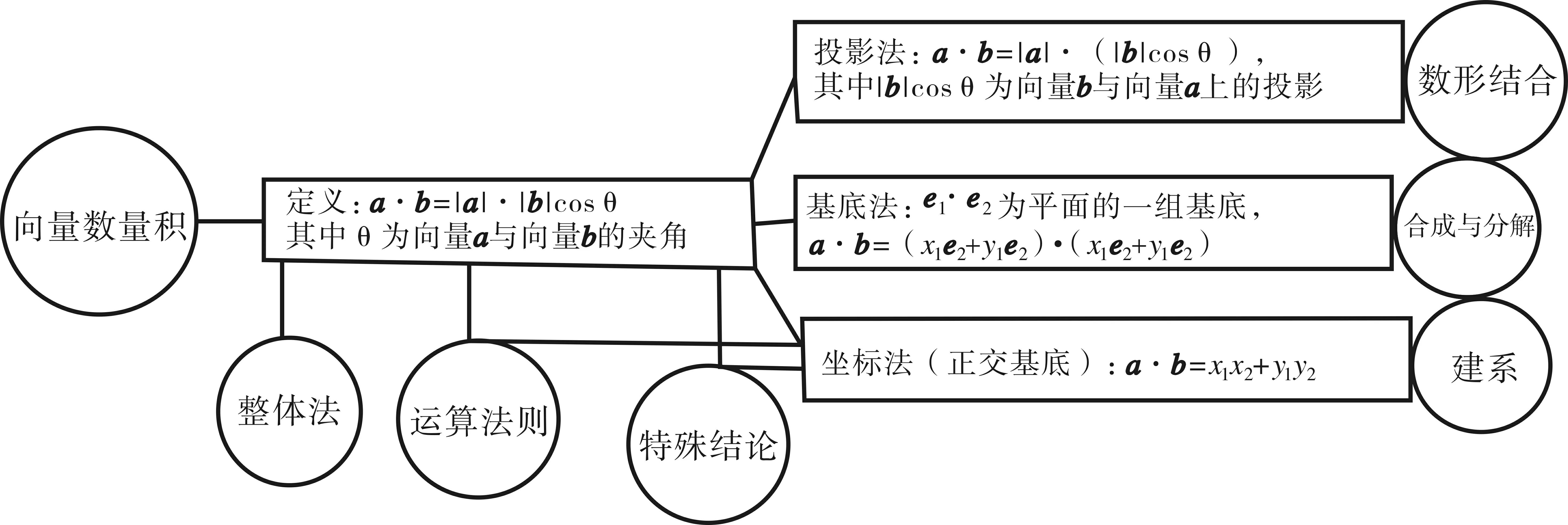
自我梳理向量數量積有多種運算方法，破解渠道，值得細細思考.下面是向量數量積的知識網絡圖.

優化二上述方法先合成與分解，再利用數量積的定義，結合余弦定理，化簡要使得兩向量有一個共同的點，這樣夾角的余弦才能借助余弦定理求得.據此可在第一次合成與分解時實現，避免二次麻煩.

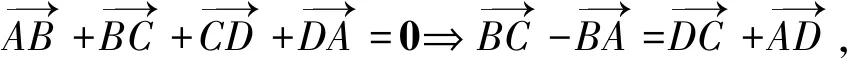
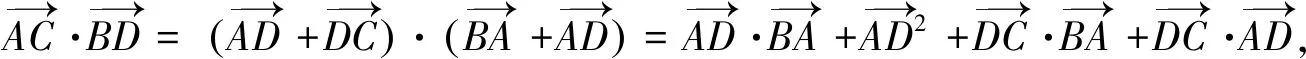
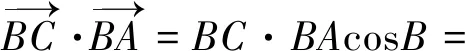
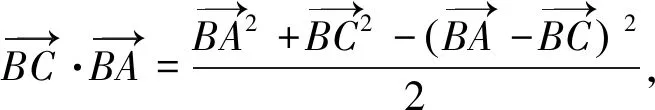
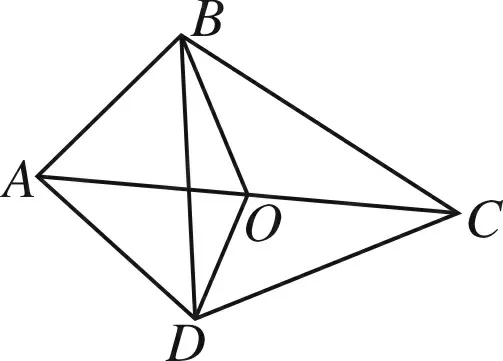
圖3

優化七從上述的解題過程可以發現，O為平面上的任意一點，那么可以嘗試在四邊形的四個頂點之中選擇將更簡單.選擇點A進行嘗試.

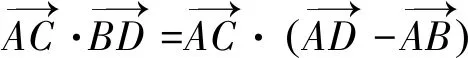
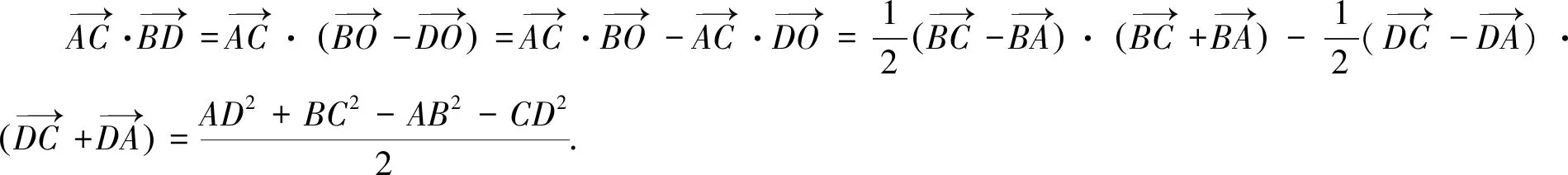
注一次次的深入思考過程中，解法更靈活，既簡化了運算，更滲透了本質，真是美的享受.

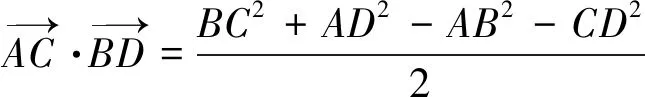
優化九坐標法

設∠ABC=θ，以B為坐標原點，BC邊所在直線為x軸，建立平面直角坐標系xOy，

則A(cosθ，sinθ) ，C(4，0).設D(x,y)，

則由AD=3，CD=2，得

將兩式相減，即得(4-cosθ)x-ysinθ=10，

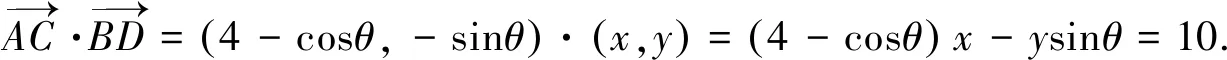
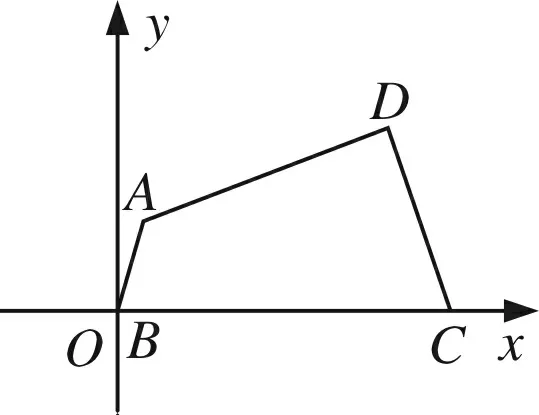
圖4

注經分析可知本題的圖形是一個動態圖形，而解題目標是求定值，故可采用特殊化策略，如取θ=90°.

優化十

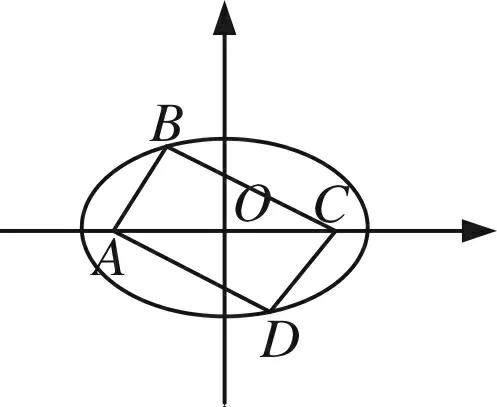
圖5

因為AB+BC=CD+DA=5,不妨構造焦點在x軸上的橢圓(如圖)，

設B(x1,y1),D(x2,y2)，則AB=1,BC=4,CD=2,DA=3，利用焦半徑公式，得

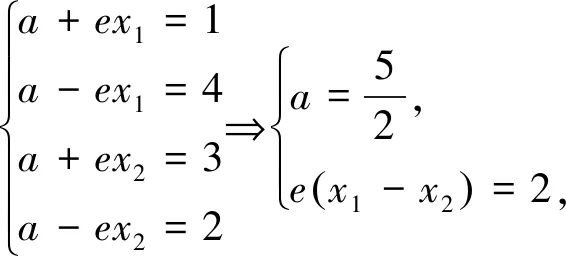
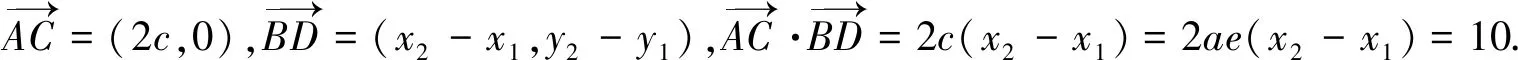
自我再梳理通過上述優化的過程，有很多感受，探究優化中學到很多新的技能，對今后的學習有很大的幫助，下面來完善一下數量積最初的知識網絡圖吧.

基本方法的理解與靈活運用還需在解題過程中得到深刻，解題能力的提升必須依靠解題，筆者百度了下面幾道類似的題目，牛刀小試，希望能夠日漸鋒利.

圖6

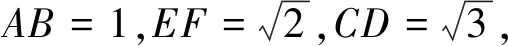
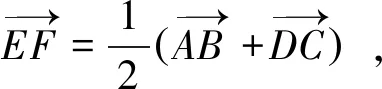
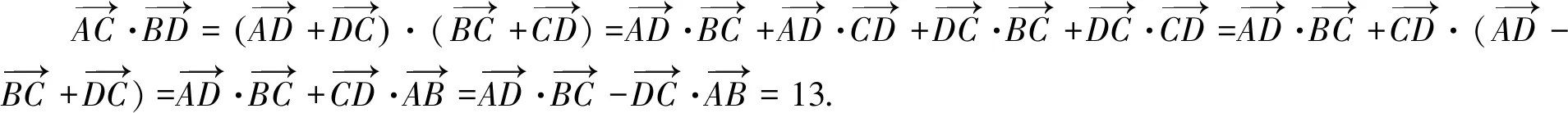
(1)

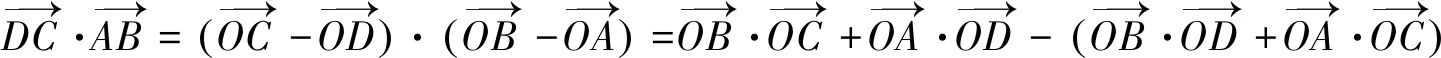
(2)

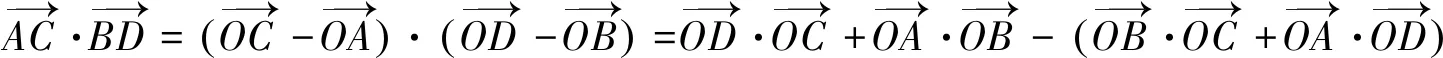
(3)

只要將(1)-(2)可得(3)

方法三對角線定理

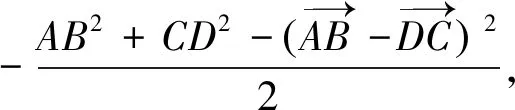
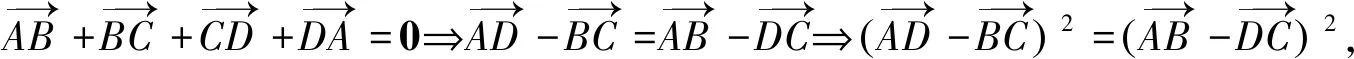
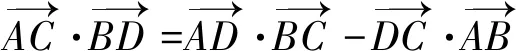
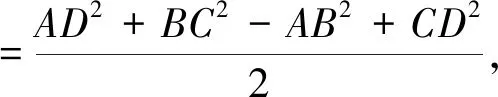
通過牛刀小試題的處理，進一步加深了數量積相關知識的理解，熟練應用數量積知識網絡圖處理數量積相關問題，使知識方法進一步系統化、網絡化，讓思維可視，讓發散更自然.我愿意在數學探究這條道路上一直走下去，享受其中的樂趣.