從一道高考圓錐曲線解答題談解析幾何備考策略

甘肅省秦安縣第二中學(xué) (郵編：741600)

甘肅省秦安縣郭嘉鎮(zhèn)槐川初級中學(xué) 劉娟娟 (郵編：741600)

2018年全國高考數(shù)學(xué)新課標卷Ⅲ理科第20題總體上保持了近幾年來的命題特色，是一道直線與橢圓的位置關(guān)系問題，以中點弦問題為依托，主要考查了直線與橢圓的位置關(guān)系以及等差數(shù)列，體現(xiàn)了高考試題在知識交匯處命題的特點，考查了數(shù)形結(jié)合思想，也考查了考生的數(shù)學(xué)抽象、邏輯推理和數(shù)學(xué)運算的核心素養(yǎng).其中第(Ⅰ)問容易入手，第(Ⅱ)問難度較大，前后兩問之間有很好的梯度性，具有很好的選拔功能.本文對這道試題進行解法、源頭和變式探究，并結(jié)合這道試題來談一下解析幾何的備考策略.

1 真題再現(xiàn)

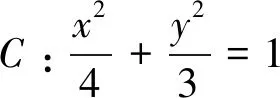
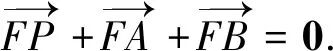
2 解法探究

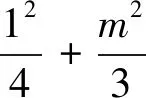
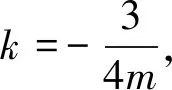
證法2 設(shè)直線l的方程為y=kx+t，設(shè)A(x1,y1)，B(x2,y2)，

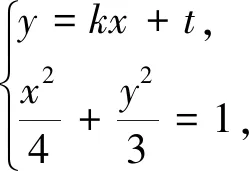
(4k2+3)x2+8ktx+4t2-12=0，

則△=64k2t2-4(4t2-12)(3+4k2)>0，得4k2+3>t2

①

由韋達定理以及中點坐標公式，可得

因為m>0，所以t>0，k<0，且

②

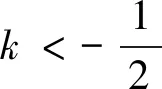
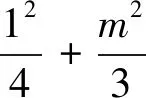
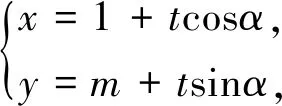
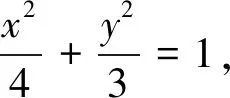
整理可得，(3cos2α+4sin2α)t2+(6cosα+8msinα)t+4m2-9=0，

由t的幾何意義知|MA|=|t1|，|MB|=|t2|，因為點M在橢圓，這個方程必有兩個實根，由根與系數(shù)關(guān)系，得

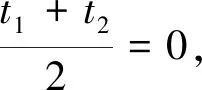
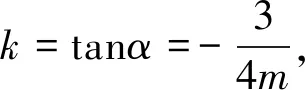
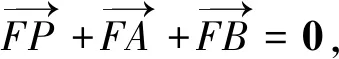
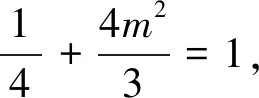
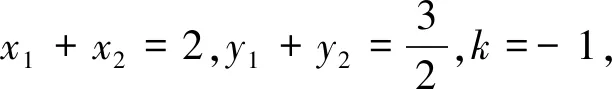
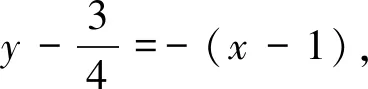
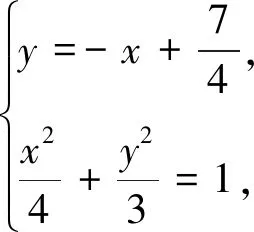
28x2-56x+1=0，解得

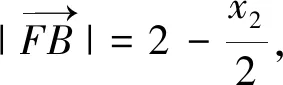
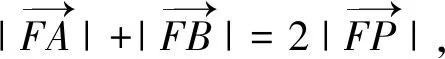
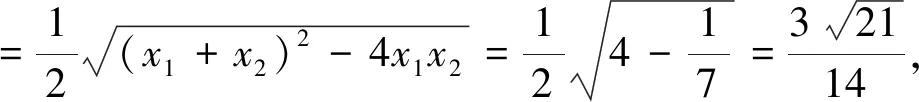
解法賞析第(Ⅰ)問的證法1運用了點差法，點差法可以看成破解圓錐曲線中點弦問題的通法；第(Ⅰ)問的證法2運用了參數(shù)法，將直線方程和橢圓方程聯(lián)立后運用韋達定理和坐標運算，發(fā)揮判別式的制約作用；第(Ⅰ)問的證法3運用了參數(shù)方程法，令人耳目一新.第(Ⅱ)問既運用了點差法，也運用了參數(shù)法，利用等差中項的定義證明了等差數(shù)列，體現(xiàn)了函數(shù)與方程、化歸與轉(zhuǎn)化的思想.從以上可以看出，選擇不同的解法，運算的繁瑣程度不同.本題中的運算是借助幾何圖形進行的代數(shù)運算，考查了運算求解能力，體現(xiàn)了數(shù)學(xué)運算的核心素養(yǎng).解析幾何的運算通常集“繁、長、巧”于一體，讓很多同學(xué)望而生畏.究其原因，主要是同學(xué)們在運算長度的判斷上出了問題：不能預(yù)估選擇的解題方法會有怎樣的運算及運算長度.若在解題過程中，同學(xué)們能認識到解題環(huán)節(jié)產(chǎn)生的運算，并通過分析進行合理的調(diào)控，更深入地理解算理，這樣才可以提高運算的靈活性.

3 源頭探究

“問題那得清如許，為有源頭活水來” .以下對這道題探源，揭開這道題的“廬山真面目”.

3.1 源頭1

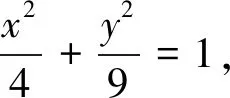
(1)這組直線何時與橢圓相交？

(2)當它們與橢圓相交時，證明這些直線被橢圓截得的線段的中點在一條直線上.

真是“眾里尋它千百度，那題卻在課本習(xí)題處”,也體現(xiàn)了“高考題出于課本，高于課本”.

3.2 源頭2

在歷年高考真題中，也有該高考題的“影子”，2015年全國高考新課標卷Ⅱ理科第20題為：

已知橢圓C：9x2+y2=m2(m>0)，直線l不過原點O且不平行于坐標軸，l與C有兩個交點A、B，線段AB的中點為M.

(1)證明：直線OM的斜率與l的斜率的乘積為定值；

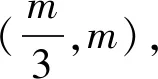
通過探源，我們發(fā)現(xiàn)這道題既可以看成改編自課本，也可看成改編自歷年高考真題.

4 變式探究

圓錐曲線有太多類似的性質(zhì)，可模仿命題者的思路，對以上試題進行改變，得到了一道變式題.

變式已知斜率為k的直線l與拋物線C：y2=4x交于A、B兩點，線段AB的中點為M(1,m)(m>0).

(1)證明：k>1；

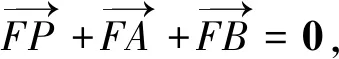
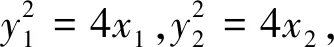
(y1+y2)(y2-y1)=4(x2-x1)，

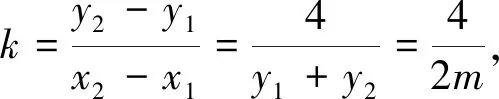
因為點M在拋物線C內(nèi)，所以m2<4，結(jié)合m>0，所以01.

(2)由題設(shè)可得F(1,0)，設(shè)P(x0,y0)，

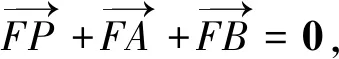
所以x0=1，y0=-2m，

因為點P在拋物線C上，所以(-2m)2=4，所以m=1，所以P(1,-2)，k=2.

所以直線l的方程為y-1=2(x-1)，即

y=2x-1，

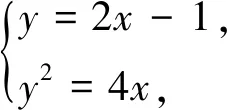
4x2-8x+1=0，

由根與系數(shù)關(guān)系，可得

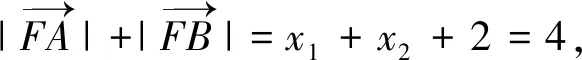
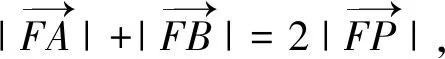
5 對2019年備考策略的建議

5.1 回歸課本，夯實基礎(chǔ)，構(gòu)建知識網(wǎng)絡(luò)

近幾年來高考數(shù)學(xué)試題遵循“大穩(wěn)定，小創(chuàng)新”的方針，重視基礎(chǔ)知識和基本技能的考查.同時，通過上面對圓錐曲線真題的分析，發(fā)現(xiàn)源自課本.因此回歸課本應(yīng)貫穿圓錐曲線復(fù)習(xí)的自始至終.因為課本是數(shù)學(xué)知識的“生長地”，課本是高考復(fù)習(xí)的“根據(jù)地”，課本是高考試題的“策源地”，回歸課本是高考復(fù)習(xí)的起點，研究課本，就是要看考題與課本的關(guān)系，從高考的要求出發(fā)，把課本熟化，公式定理能信手拈來，基本題型能“借題發(fā)揮”.在回歸課本的基礎(chǔ)上，要著重強化對知識的梳理、優(yōu)化知識結(jié)構(gòu)、構(gòu)建知識網(wǎng)絡(luò).

5.2 注重通性通法

高考中解析幾何試題通常是對常見題型進行加工改編，通過對基礎(chǔ)知識的整合、變式和拓展，從而加工為高立意、新情境、巧設(shè)問的解析幾何問題，堅持新題不難，難題不怪的命題方向.這要求同學(xué)們要通過高中學(xué)習(xí)掌握基礎(chǔ)知識、基本概念、基本技能和基本數(shù)學(xué)思想的應(yīng)用，通過對教材中基本例習(xí)題的變通，積累一些常規(guī)基本問題的解法，反復(fù)體會其中蘊含的思維方法.把解題方法提高到數(shù)學(xué)思想的高度，提高分析和解決綜合問題的能力.例如，對于圓錐曲線的中點弦問題，要優(yōu)先考慮點差法；對于求橢圓離心率的題目，大多要利用數(shù)形結(jié)合法，結(jié)合橢圓的定義求解.對于拋物線的焦點弦和焦半徑問題，要根據(jù)焦點弦公式和焦半徑公式，結(jié)合拋物線定義求解.在求橢圓的弦長時，利用弦長公式，運用設(shè)而不求的方法.

5.3 提高數(shù)學(xué)運算求解能力，發(fā)展數(shù)學(xué)運算的核心素養(yǎng)

高考數(shù)學(xué)答卷中反映出的問題之一是部分考生的運算能力差，是最頭疼的事，有的考生想得很好，但運算過不了關(guān)，一道長題一開始就錯，而自己沒有自查能力，一直錯到底，多么可怕呀！

而出錯的原因往往很簡單，就是諸如一個負號的問題，直線方程和圓錐曲線方程聯(lián)立化簡整理時出錯，太可惜.數(shù)學(xué)運算能力的培養(yǎng)不僅僅是高三復(fù)習(xí)的事，應(yīng)該貫穿于高中數(shù)學(xué)學(xué)習(xí)的始終.特別是解析幾何解答題，綜合性強，代數(shù)推理要求高，運算求解能力要求高，繁雜和冗長的計算是必不可少的，因此同學(xué)們要通過強化數(shù)學(xué)思想方法，特別是函數(shù)與方程、數(shù)形結(jié)合、等價轉(zhuǎn)化、分類討論等理解算理，從而提高自己的運算求解能力，發(fā)展自身的數(shù)學(xué)運算核心素養(yǎng).

5.4 研歷年高考真題，體會命題專家的命題思路

高考試題不僅具有選拔功能，還具有很好的教育功能.高考試題凝結(jié)了命題專家的智慧與匠心，具有較強的原創(chuàng)性與指導(dǎo)意義，有利于考查考生的探究意識與創(chuàng)新精神.有部分高考試題是往年真題的同類題或“翻版”， 因此，在平時的學(xué)習(xí)中，對高考試題進行適當發(fā)散研究，不僅可以理清脈絡(luò)，把握高中數(shù)學(xué)主干知識，避免高三復(fù)習(xí)的隨意性、盲目性，而且可以有效訓(xùn)練同學(xué)們自己的思維，提高探究能力，培養(yǎng)創(chuàng)新意識.

5.5 重視新增知識，關(guān)注知識交匯

對新增的極坐標與參數(shù)方程等知識，要引起足夠的重視，比如，前面真題第(Ⅰ)問的證法3就是用參數(shù)方程做的，在高考中如果沒想到其他方法，選用參數(shù)方程法，也是很好的.同時，要關(guān)注知識交匯，本文開頭的高考真題，可以看成是解析幾何與向量、等差數(shù)列的交匯，從歷年高考試題來看，有時，解析幾何真題也與導(dǎo)數(shù)、不等式、三角函數(shù)等交匯，也充分體現(xiàn)了考試中心提出的“應(yīng)更多地從知識網(wǎng)絡(luò)的交匯點上設(shè)計題目，從學(xué)科的整體意義、思想含義上考慮問題”的思想.