瞄準通法 凸顯過程
——記一節高三一輪后的復習課

安徽省淮南市教育局中小學教研室 (郵編：232001)

1 問題提出

《普通高中數學課程標準(2017年)》明確指出“高中數學學習活動不應只限于接受、記憶、模仿和練習，還應倡導自主探索、動手實踐、合作交流、閱讀自學等學習數學的方式.”教學目標的實現要靠學生在學習過程中不斷積累基本的活動經驗，并運用已有數學知識及其所蘊含的數學思想方法去解決問題，由此在此過程中感悟數學學習的價值和作用，提高學生的數學素養.

歷年高考數學考試大綱均明確將“注重通性通法，強化特殊技巧”作為一條重要命題原則.這就是要求教師提高對所教內容的理解水平，增強辨別和判斷能力，并在數學中引導學生去分析、總結、體會哪些是“雕蟲小技”，哪些是“通性通法”，逐步提高學生的解題能力和數學素養，最終落實數學學科的育人功能.

高三教學后期(一輪已結束)盡管復習已到位，但需要對一系列相對零散知識與方法進行重組，構緯聯經，形成網絡.但正是因為如此，教師的教學組織更要彰顯“過程”與“通法”，充分調動學生的主動性.以下結合筆者聽評的一節高三復習課，以求“管中窺豹”，并向各位求教與匯報.

2 課堂實錄

出示一道經典例題：

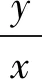
師：請問這道如何求解，請大家發表看法.

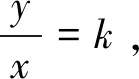
師：這個方法不錯，不妨稱之為判別式法(投影生1解題過程).

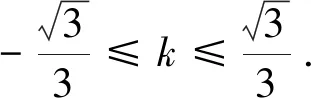
師：本題還有其它解法嗎？

生2：由生1的設法y=kx表示直線，(x-2)2+y2=1表示圓，故還可以利用直線與圓的位置關系來求解.

師：這個想法很自然，我們稱之為幾何法(投影生2的解題過程).

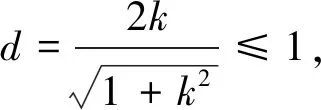
師：本題是否僅有此兩種解法呢？

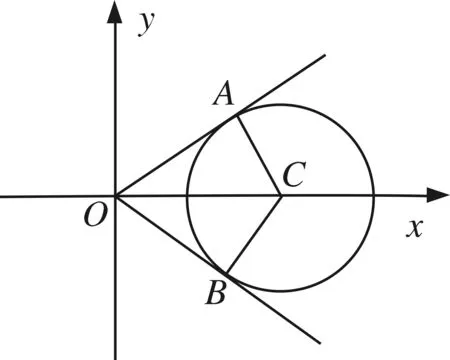
生3：還有更簡潔解法，幾乎可以“秒殺”！

師：還有如此玄妙的解法？趕快貢獻出來與我們一同分享吧！

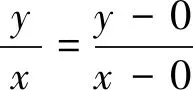
注意|OC|=2,|AC|=1,則∠AOC=∠BOC=30°，故

師：這個方法以形助數，借形解數，妙不可言，稱之為數形結合法.本題已有三種解法，估計差不多了吧？

生4：還有一種解法.

師：請你說說看.

生4：可利用圓的參數方程進行三角換元解決(投影生4的解法).

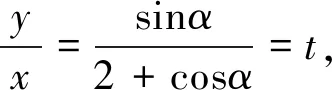
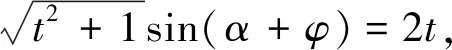
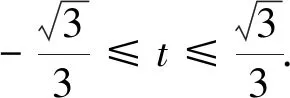
師：剛才大家一共找到四個辦法共同解決了一個問題，可謂“異曲同工”.那么在以后解題應該如何選取最有效的方法呢？接下來再看幾個題目，請大家思考，討論下列各題可采用什么方法？(引導學生先討論再回答)

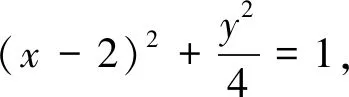
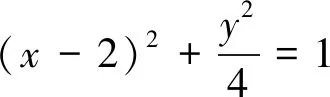
師：為何不用幾何法？

生5：因為目前我們還不能從幾何直觀上判定直線與橢圓位置關系.

師：很好！那么“數形結合”你是如何求解呢？

生5：過原點向橢圓引切線，求出切線斜率.

師：如何求切線斜率？

生5：利用判別式.

師：那么該“數形結合法”本質上說仍是判別式法.故本題通法為“判別式法”與“三角換元法”.(解題過程略)

變式2 若實數x、y滿足x2+xy+y-3=0,試求2x+3y的最值.

生6：本題只能用判別式法.

師：請說一說你的理由.

生6：因為x2+xy+y-3=0只是一個二元二次方程，其幾何意義并不清楚.

師：很好！看來“判別式法”是一個無所不能的好辦法，應該算是我們常談的“通性通法”，那么它會不會也有“失敗”的時候呢？

變式3 若實數x、y滿足(x-2)2+y2=1,試求x2+y2+2x-4y的最值.

師：這道題可用判別式嗎？為什么？

生7：不可以，因為所求結果不是一次式，不能進行消元.

師：那么它該如何求解呢？

生7：可用三角換元(投影生7的解法)

令x=cosθ,y=sinθ,

原式=(2+cosθ)2+sin2θ+2(2+cosθ)-4sinθ=9-2(2sinθ+3cosθ)

生8：本題也可用數形結合，因為x2+y2+2x-4y=(x+1)2+(y-2)2-5，其中

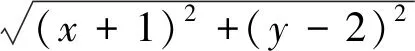
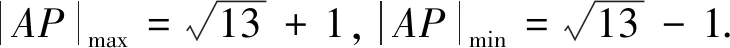
師：生8解法很有思想，數形結合，魅力無窮.

生9：剛才生7說x2+y2+2x-4y不是一次式，事實上，所求代數式可轉化成一次式求解，故還可用判別式.

師：真的嗎？說說你的發現.

生9： 由(x-2)2+y2=1，知x2+y2=4x-3，故x2+y2+2x-4y=6x-4y-3，可用判別式求解.

師：非常正確，轉化成功，這個方法老師都沒想到！讓我們為他鼓掌!(掌聲四起)

課堂小結：

本節課我們集中研究了在二次方程(一般不含xy項)限制性條件下，求代數式的最值問題.主要結論小結如下：

若被求代數式為線性(或可轉化為線性)，則可用“判別式”法求解，即“判別式”法是求解該問題的“通性通法”.

若已知條件可轉化成圓或橢圓方程，則可考慮采用三角換元求解：若被求代數式又有明顯的幾何意義(斜率與距離)也可用數形結合求解.

3 感悟升華

3.1 “一輪后”復習也要重視“過程”

應該說隨著課程改革的推進，教師在新授課的教學中，教師的教學觀或多或少都發生了改變，探究活動，合作學習也常見于課堂.然而在高三一輪后復習備課的教學中，課堂再次被教師獨霸，常見的教學是教師提前編寫講義，發給學生練習(或測試)，教師結合學生錯誤多的地方進行重點訂正.如此簡單隨意的教學，把習題課變成訂正課，很難保證復習效率.即便在重點題型講解上，也只是在炒剩飯，突出表現在以下兩方面：一是對同一個題目采取一題多解，各種解法平行推進，以教師的講解代替學生的思維，再以類似題進行固化的訓練.然而一旦題目稍有變化，學生便感到“十八般武藝，樣樣不通”，教學的效果大打折扣.二是未能很好地將相關知識點進行“串聯”，形成有機的整體，造成學生認知上的困難，學生的能力并未真正提高.本節課從一個簡單而又不失經典的題目入手，全方位展示該題的多種解法，每一種解法都不是教師給出，而是由學生根據提議和結論，不斷進行升級與改造，充分給學生時間，做足“過程”.為了進一步讓學生逐個感悟到各解法的適用對象，課堂上將原題進行適當的變式，制造沖突，讓學生時刻處于興奮狀態，讓復習課也充滿新鮮感.

“灌輸”雖然也可以讓學生獲得知識，但失去了直覺、感悟和樂趣；而關注“過程”的教學在讓學生獲得知識的同時，卻在發展著學生的思維，感受著數學的魅力，在生命層次上體驗學習的樂趣,感悟數學的教育價值.

3.2 “一輪后”復習更要突出通法

本節課的題目引例雖然簡單，但方法多樣，倘若不慎，會讓學生有“錢多不知如何花之感”.為此，在后續的教學安排中，不斷變化條件與問題，最終讓學生體會到“判別式法與“三角換元”作為解決此類問題的“通性通法”的威力與“魅力”！雖然問題較多，但由于問題設計條理清晰、層次清楚、設問自然，會有“忽如一夜春風來”的頓悟.

誠然，“通法”不能由教師簡單地告知，而應當讓學生去親自體驗與感悟.本節課教師似乎沒有給學生任何解題“妙招”，而只是在追問學生“你是怎樣想的”“還有什么想法”“為什么不能這樣想”“為什么可以這樣想”這些追問其實引導學生挖掘精彩背后的“通法”之源，充分暴露學生的思維過程，加深學生對知識的理解和運用，用“火熱的思考”去替代“冰冷的美麗”，從而提升學生思維的品質.

3.3 學生是“一輪后”最具活力的資源

在高三復習后期(一輪復習已結束)，學生對高中數學知識體系、思維方法都有了較系統的掌握.加之，他們對同一個問題思考角度不同，一定會帶來不同的解題策略與方法，正所謂“眾人拾柴火焰高”.在教學中，教師應注重對課堂最具活動的資源——學生的開發.如教師可以通過設置恰當的情境，讓學生去探索、討論、講解，對于同一個問題，引導學生從多個角度去分析探究，鼓勵一題多解；對于同一類問題，引導學生從中抽象概括出本質屬性，總結規律和方法,強化通性通法，最終提升學生的解決問題的能力.