一類條件為abc=1的不等式

廣東省中山市中山紀念中學 (郵編：528454 )

在不等式中,經常遇到條件為abc=1的不等式,比如越南不等式專家Can-Hang的一個經典結論,本文稱之為定理1.

在證明定理1之前,首先給出本文要用到的不等式.

1 三元均值不等式及常見結論

(2)a、b、c∈R,a2+b2+c2≥ab+bc+ca;

(3)a、b、c∈R,(ab+bc+ca)2≥3abc(a+b+c).

2 三元柯西不等式及常見結論

于是得到以下結論:

有了結論1,筆者利用柯西不等式并結合待定系數法來證明定理1.

由柯西不等式有

利用定理1,可快速地證明例1.

由xyz=1和定理1得證.

證明由柯西不等式有

(2)經過簡單變形,可得到以下式子:

證明由柯西不等式有

利用柯西不等式證明此類條件為abc=1的不等式的關鍵是創設應用柯西不等式的條件,配合一定的變形、構造技巧,這樣可使復雜問題簡單化,達到事半功倍的效果.若所證不等式的結構較簡單,注意到柯西不等式的結論中分子部分的指數為偶數,此時無需利用待定系數法,經過簡單嘗試和配湊即可利用柯西不等式變形,并利用結論1或均值不等式解決問題.

證明由柯西不等式有

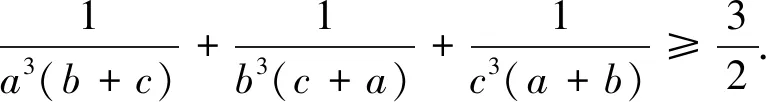
證明由柯西不等式有

證明由柯西不等式有

證明由柯西不等式有

所以不等式得證.

不等式證明往往沒有通法,也沒有固定的模式,方法巧妙而靈活.均值不等式和柯西不等式是兩個非常重要的不等式,也是證明其他不等式常用的方法和工具.下面再給出幾個條件為abc=1的不等式問題,并利用均值不等式和柯西不等式來證明.

證明由柯西不等式，有

故不等式得證.

下面摘選一些條件為abc=1的不等式,留給有興趣的讀者.

設a、b、c>0,且abc=1,證明: