聚焦思維方法 指向問題本質
——對一道聯賽題的探究與思考
浙江省溫嶺中學 (郵編:317500)
2017年9月10上午全國高中數學聯賽一結束,筆者當日下午就參加了浙江賽區在杭州的閱卷工作.對第9題的批閱和同事的討論,激發了對該題的深入探究.
1 試題展示

2 試題特點
本題作為解答題第1題(解答題共3題),它源于平時高考范圍內的常見題,所涉及的知識不超過高考要求,但在有些處理手法上略有提高.本題語言簡潔、解題入口寬、層次多,具有非常明顯的區分度.數學素養一般的考生,通過對問題的合理分析,運用常規的討論等方法,能夠得到自己理想的結論,但是時間的成本會較大;而數學素養好、思維品質好的學生,能快速直達問題的本質,此題的本質在于分析拋物線的“陡峭程度”.因為k、m其實只影響f(x)=x2-kx-m的圖象位置而不影響其形狀,故本題其實是討論f(x)=x2的圖象中使得函數值差距不超過2的最長區間,即在分析拋物線的“陡峭程度”.
3 多視角下的方法探究
視角一三點法的視角
令f(x)=x2-kx-m,x∈[a,b], 則f(x)∈[-1,1], 于是
f(a)=a2-ka-m≤1
①
f(b)=b2-kb-m≤1
②
③
由 ①+②-③×2,得



視角二對稱軸討論的視角
令M=f(x)max-f(x)min, 則M≤2 對任意x∈[a,b]恒成立.


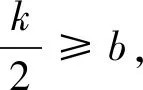
M=f(a)-f(b)=(a-b)(a+b-k)
≥(a-b)(a+b-2b)=(a-b)2,

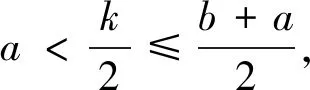
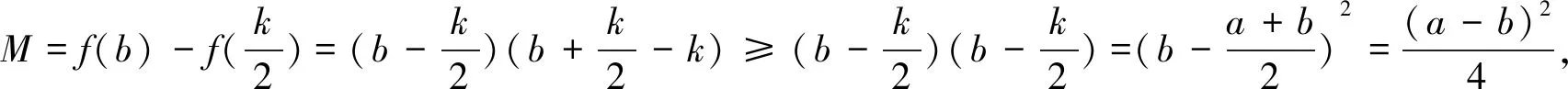
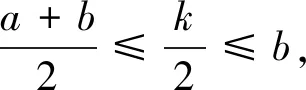


點評利用對稱軸與區間的討論,得出函數在區間上的單調性,然后得出M的表達式,再利用不等式放縮即可.大多數考生會從這個角度去思考和解題,他們能寫出討論的全部4種情況或者其中的幾種情況. 一些優秀的學生會把(3)、(4)兩種情況合起來:
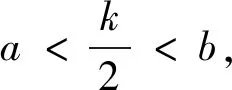
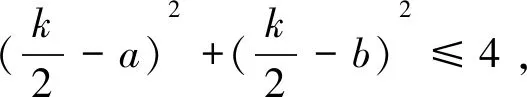

視角三最小值討論的視角
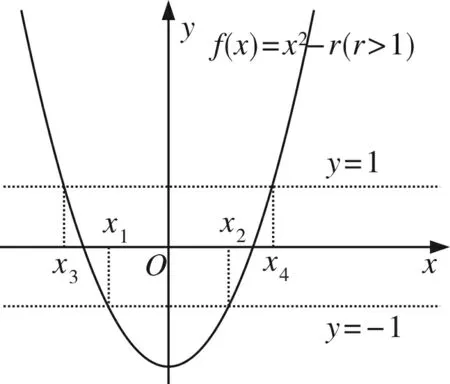
圖1
不妨設f(x)=x2-r,x∈[a′,b′],b-a=b′-a′ ,下面對x∈R時,討論f(x)的最小值,
(1)若f(x)min<-1, 即r>1,



(2)若-1≤f(x)min≤1, 即-1≤r≤1,

圖2

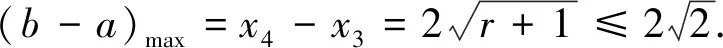
(3)若f(x)min>1, 則|f(x)|≤1 無解.

點評首先把f(x)視為f(x)=x2-r,這需要對二次函數有本質的理解,學生需要較好的數學素養,這樣處理簡化了后續的運算.其次此解法的本質是通過研究f(x)的圖象與直線y=1 或y=-1交點的橫坐標之差,來刻畫b-a的范圍.從具體的背景中抽象出一般的數量關系,概括出問題的本質,再從直觀的圖形角度來解決問題,認識了數與形的關系,在解決問題過程中,有利于培養學生直觀想象的核心素養. 對上面的解法可進一步優化為:不妨設f(x)=x2-r,對?x∈[a,b],均有|f(x)|≤1.
下面對r進行討論.
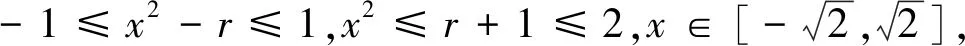

當r>1 時,由|f(x)|≤1,得-1≤x2-r≤1,r-1≤x2≤r+1,
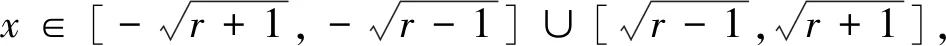
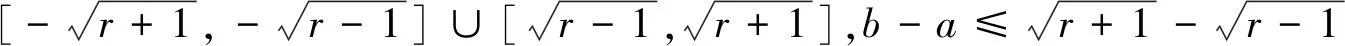

視角四反證法的視角
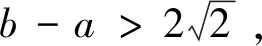
(1)若k≤2a或k≥2b, 則a+b-k≥b-a或a+b-k≤-(b-a),
|f(a)-f(b)|=|b-a||b+a-k|≥|b-a|2>8>2,
(2)若2a (3)若a+b 綜上①、②、③知總存在x1、x2∈[a,b], 使|f(x1)-f(x2)|>2. 視角五函數凹凸性的視角 -1≤x2-kx-m≤1 對?x∈[a,b] 恒成立,因為y=x2-kx-m為下凸函數, 即0≤(a-b)2≤8, 視角六競賽的視角 由拉格朗日插值恒等式知 f(x)=x2-kx-m 比較上式兩邊x2的系數,得 整理得 (1)此題雖有著“入手易,解法多”的特點,但部分考生仍感覺力不從心.因此在平時的教學中應關注學生思維,重視問題的本質.張奠宙教授曾說:“數學教學的有效性關鍵在于對數學本質的把握、揭示和體驗”.因此在平時教學中盡量留給學生足夠的時間讀題、審題,在這個過程中讀出若干思維角度,審出題目結構,理解問題本質. (2)數學教學是“慢”藝術,若短時間內把所有好的數學思想方法打包發給學生,往往因空間不足而無法解壓.因此,在教學中教師要敢于等待學生,陪伴學生重筑數學知識的形成之路,而不要在某些經典知識上一筆帶過. (3)平時所謂的難題通常對多個知識點進行交叉和互融考察,數學素養較高的學生遇到難題時會把多種通法綜合在一起,創造出含有“技巧性元素”的方法.因此,在平時的教學中,注重對知識“通性通法”的教學,通法就是遵循數學的思維特征分析問題和解決問題,只要對問題解決的通性通法熟練、高效,某些技巧性方法自然會應運而生. (4)注重高中數學與拓展知識之間的聯系.比如函數的凹凸性、不動點理論、拉格朗日插值恒等式、極限思想等,其實平時試題中常會出現用琴生不等式秒殺的問題等.再如極限思想在函數零點判斷問題中會常用到.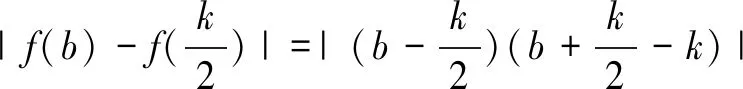
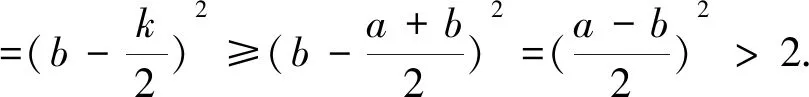


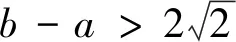
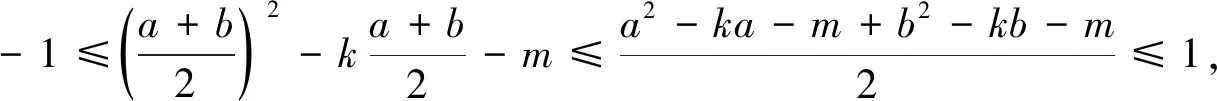



4 思考與建議

