一次現場命題比賽的全記錄

浙江省金華市第六中學 (郵編：321000)

為了加強新高考背景下數學復習的信息交流，增進數學復習的經驗共享，增強復習的針對性和實效性，提升教師的命題能力，浙江省金華市教研室決定于11月27日13:30-16:30在浙師大附中舉辦金華市首屆高中數學現場命題比賽.由舉辦方提供命題背景和命題方向，以校為單位(每單位三名高三教師)組隊報名參加，比賽自帶電腦，可帶資料，但比賽時不允許上網.筆者有幸參加了此次現場命題比賽，并榮獲金華市一等獎．經過抽簽，得到如下命題材料.

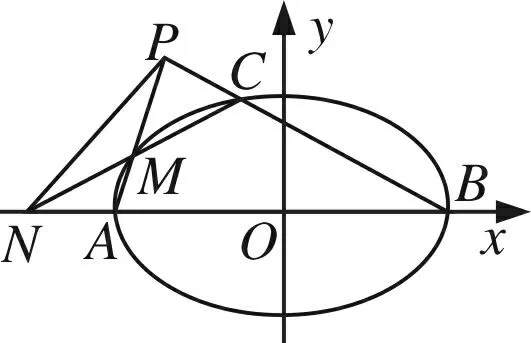
解析幾何現場命題試題

要求請你改變“A、B是橢圓長軸上的兩個頂點”狀態為“某種符合條件的兩點”，命制一道具有浙江特色的高考題，并做簡要解答. 現將本次現場命題比賽活動記錄如下，供同行批評指正．

1 背景解讀

圖1

借助幾何畫板對滿足上述條件的問題進行了演示，立馬就可以測算出數值，如圖1所示，圖形變化過程中數量關系的變化(哪怕是微小的變化)也可以直觀地顯示出來. 筆者欣喜地發現，在連續改變交點P坐標數值時，不影響結論成立. 其實這是一個與圓錐曲線極點和極線有關的一個統一等差定理[1].

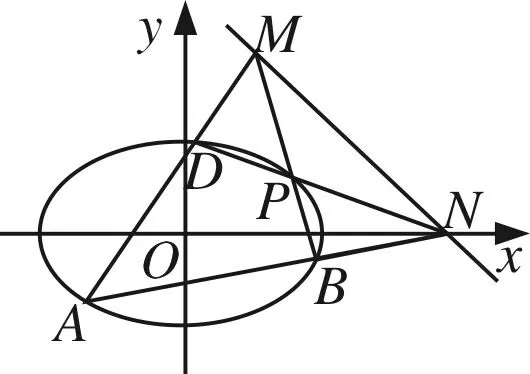
圖2

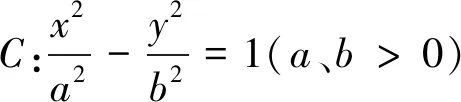
定理3 點A、B、D、P是拋物線C:y2=2px(p>0)上四點，直線AB、DP交x軸于點N，直線AD交BP于點M，設AD、BP、MN的斜率為k1、k2、k3，則k1+k2=2k3．

2 題源追溯

圖3

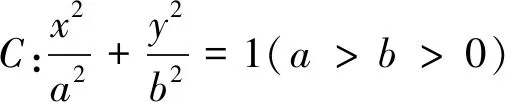
(1)求橢圓C的方程；

(2)AB是經過右焦點F的任一弦(不經過點P)，設直線AB與直線l相交于點M，記PA、PB、PM的斜率分別為k1、k2、k3.問：是否存在常數λ，使得k1+k2=λk3？若存在，求λ的值；若不存在，說明理由．

題源2 (2013年高考江西卷文科20題)

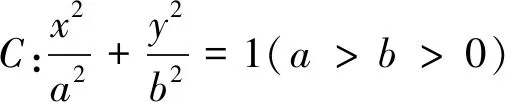
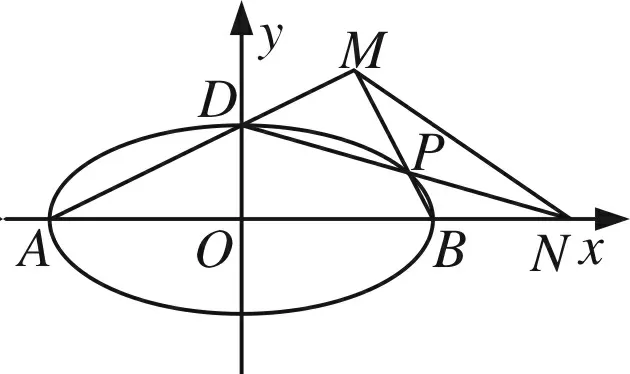
圖4

(1)求橢圓C的方程；

(2)如圖4所示，A、B、D是橢圓C的頂點，P是橢圓C上除頂點外的任意點，直線DP交x軸于點N，直線AD交BP于點M，設BP的斜率為k，MN的斜率為m，證明：2m-k為定值．

每年的高考試題似乎都出乎意料，卻又在情理之中．2013年高考江西文理卷中的解析幾何解答題更是堪稱經典，賞析之余，無不佩服命題者的深厚功底和良苦用心．對這些題進行深入研究，并對其進行改編是命制高考模擬試題的常用著力點．

3 命題歷程

3.1 立意與選材

立意是確定試題的編寫意圖，明確考查目的(考查哪幾種能力？哪種能力為主？哪種能力為兼顧？考查哪個學科分支？考查哪部分內容？等等)，立意是核心，選材應服務于立意．根據抽簽材料上的要求，筆者擬命制一道圓錐曲線的綜合試題，著重考查直線方程、直線斜率及直線與圓錐曲線相交等知識，旨在考查學生的邏輯推理、直觀想象、數學運算等核心素養．

3.2 聯系與搭架

波利亞說：“類比是偉大的引路人．” 圓與橢圓、雙曲線、拋物線 “同宗同源”，那么圓是否具有上述類似結論成立？同時受到題源2定值問題的啟示，特初擬了如下試題．

命題1 已知圓O:x2+y2=1與x軸交于A、B兩點，與y軸交于點C,M是圓O上任意一點(除去圓O與兩坐標軸的交點)．直線AM與BC交于點P,直線CM與x軸交于點N,設直線PM、PN的斜率分別為m、n，求證：m-2n為定值．

為了減少運算的盲目性，借助幾何畫板對滿足上述信息的問題進行了演示，發現m-2n始終為定值1，從而確保了命題的正確性．定值問題求解方法通常有兩種：一是特殊值求法，即將問題條件特殊化，再證明所特殊化后的定值與變量無關；二是直接推理、計算，將要求的定值表示為某個變量的函數關系，再化簡這個關系消去變量，從而得到定值．本題設點為參數或設斜率為參數均可順利求解，有興趣的讀者可試一試．同時，設計試題框架時應注意主干硬朗，層次分明，從而形成坯胎．試題坯胎要具有一定的彈性和伸縮性，即題設條件便于增加或減少，提問角度可提供調換，試題難度容易調節，方便加工與調整．

3.3 加工與調整

2017年浙江高考數學試卷，打破了高考中文科生和理科生的固定思維模式，開啟了文理合卷的新篇章．解析幾何解答題作為浙江新高考次壓軸題，應充分考查學生的思維品質與學習潛能，彰顯對數學核心素養的考查要求．由命題1的解答過程來看，此題中的圓錐曲線以圓為載體，則略顯平和，缺乏必要梯度．同時受題源1、2定值問題的啟發，在隨后的多地高考模擬卷中出現了類似問題，新穎性不夠．而一道優質的試題往往是命題者研究成果的結晶，在同一個背景下，交換部分條件和結論，便可生成一道新題．筆者結合對相關題目的研究[2]，可得到以下試題．

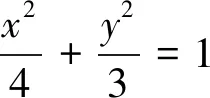
試題的加工和調整，首先確保試題的科學性和適綱性，其次是精心調節難度．難度調節必須以整卷的難度分布為依據，常用的調節方法有：改變提問方式，將結論隱藏變為探索式可以提高難度，增設中間問可降低難度；改變題設條件，條件隱蔽化或明朗化，直接化或間接化、具體化或抽象化均可調節難度；改變綜合程度，增減知識點的組合，調整解題方法的結構，變換知識和方法的綜合廣度與深度．

3.4 復核與定稿

隨著新課改的深入進行，探究存在性問題越來越受到命題者的青睞，更是高考試卷中的常客．而解析幾何中的探究存在性問題主要考查學生探索解題途徑，解決非傳統完備問題的能力，將數學知識有機結合并賦予新的情境創設而成的，要求考生自己觀察、分析、創造性地運用所學知識和方法解決問題．凸顯這一特性，命題2略顯不足，基于此，筆者作了微調，獲得了下述試題．

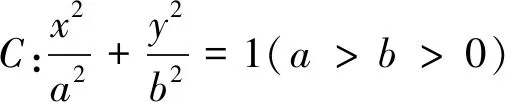
(1)求橢圓C的標準方程；

(2)若直線PA、PM、PB的斜率存在且成等差數列，試問直線AB是否過定點？若過定點，請求出定點坐標；若不過定點，請說明理由．

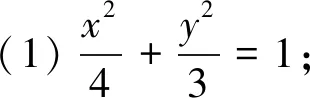
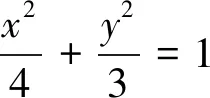
由韋達定理得

當x=4時，則y=4k+m,所以點M的坐標為(4,4k+m).

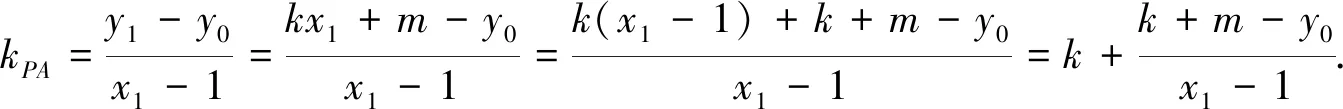
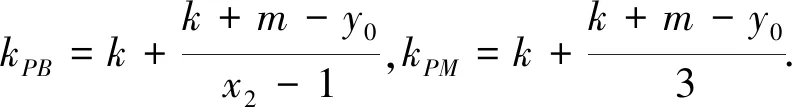
于是kPA+kPB

由直線PA、PM、PB的斜率成等差數列，得

由于l不經過點P,則k+m-y0≠0,故

化簡得(m+k)(m+4k)=0.

當m=-k時，則直線AB的方程為y=kx-k,必過定點(1,0)；

當m=-4k時，則直線AB的方程為y=kx-4k,必過定點(4,0)．

綜上，直線AB必過定點(1,0)或(4,0)．

復核工作通常需要兩人以上進行，才能防止先入為主，重新細寫答案，盡可能把各種可能的解答都寫出來進行比較，以保證達到考查目的．往往有可能發現更簡潔的解法，可能出現其考查的有效性與預先的設計意圖大相徑庭，如出現這種情況有時會前功盡棄，推倒重來．復核的另一項工作就是文字功夫，對試題的字詞句及數學符號都要一一推敲，連標點符號也不能放過．對每一個細節都得顧及，包括試題的陳述和答案的編寫，都在這一步完成．

4 點滴感悟

命題很難無中生有，教師需要解題經驗的積累，需要命題素材的挖掘，需要理念素養的熏陶，需要命題技術的提升．一道試題的成型往往意味著時間的投入和精力的付出，同時得到經驗的積累和能力的提升．只要我們能做一個有心人，勤奮鉆研，點滴積累，就會在專業上得到很大提高．