核心素養下的初中數學課堂教學的實踐與反思
——以從算式到方程(第1課時)為例

安徽省巢湖市柘皋鎮初級中學 (郵編：238062 )

在教育部近幾年所頒布的《關于全面深化課程改革落實立德樹人根本任務的意見》中，明確界定了核心素養，即學生應具備的適應終身發展和社會發展需要的必備品格和關鍵能力[1].縱觀國內，發展學生核心素養逐漸成為基礎教育界最令人矚目的熱點話題，因此，如何在初中數學課堂教學中培育學生的數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析等數學核心素養就顯得尤為關鍵.下面就以人教版初中數學教材七年級上冊的3.1節的第1課時——從算式到方程的教學實踐為例進行探討：

1 教學實錄

1.1 創設問題情境

問題1 一輛客車和一輛卡車同時從A地出發沿同一公路同方向行駛，客車的行駛速度是70km/h，卡車的行駛速度是60km/h，客車比卡車早1h經過B地，問A、B兩地之間的距離是多少?

問題2 我國民間流傳著許多趣味題，它們多以順口溜的形式表述.請大家看這樣一個數學問題：一群老頭去趕集，半路買了一堆梨，一人一個多一個，一人兩個少兩梨，請問君子知道否，幾個老頭幾個梨？

師：你會用算術方法解決這兩個問題嗎？

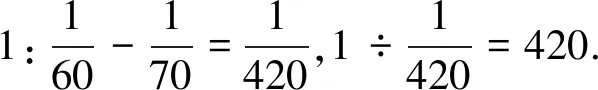
生2：2+1=3，2-1=1，3÷1=3，3×1+1=4.

師：問題中涉及哪些量，這些量之間有什么關系？

生3：問題1中的等量關系是客車比卡車早1h經過B地.

生4：問題2中的等量關系是兩次分配過程中梨的總數量相等.

師：你認為應引進什么樣的未知量？如何用式子表示問題中的相等關系？

生6：設有x個老頭，得：x+1=2x-2.

師：我們把列出的式子叫什么?你能歸納出它的定義嗎？

生7：方程，含有未知數的等式叫方程.

師：對于上面的問題，你還能列出其他方程嗎？如果能，你依據的是哪個相等關系？

生：……

設計意圖首先設置兩個問題情境以引導學生嘗試列算式，并讓他們用算術方法解決問題，然后逐步引導學生列出含未知數的式子，尋找存在的相等關系后列出方程，從而引出方程的概念，也在學生思考、交流和討論的過程中，培養了學生的數學運算能力和數學抽象能力.學生通過思考發現問題1采用算術方法較容易解決，但卻不適用于問題2，這樣便產生了新舊知識上的矛盾沖突，使學生認識到了進一步學習的必要性，更引導了學生走進實際生活去感受數學的魅力.同時，通過學生之間的合作與交流，得出了問題的多種解答方法，培養了學生的創新意識以及數學抽象等數學核心素養.

1.2 設計探究活動

活動1 比較列算式和列方程解決問題各有什么特點？

師：試比較列算式和列方程解決應用題，你有什么感悟？

生8：列算式解題有多個步驟，列方程解決問題只有一步.

生9：用算術方法解題時，列出的算式用的是已知數；而用方程解決問題時，方程中既含有已知數，又含有用字母表示的未知數.

生10：算術方法解題思考方向是逆向的，方程解決問題思考方向是順向的.

師：“從實際問題到方程”的步驟有哪些？關鍵是什么？

生11：(1)審——審題，找到已知量和未知量之間的相等關系；(2)設——設未知數；(3)列——根據相等關系列出方程.

生12：關鍵是準確找出數量之間的相等關系.

設計意圖讓學生通過對列算式與列方程解決問題作比較，分別歸納出它們的特點，從中感受到從算術方法到代數方法是數學的進步，有利于問題的解決，方程為我們解決問題帶來方便.通過引導學生歸納列方程解決問題的步驟，培養了學生由實際問題抽象出數學模型的能力以及邏輯推理、數學建模等數學核心素養.

活動2 學習一元一次的方程的定義.

師：根據下列問題，設未知數并列出方程：

(1)用一根長24cm的鐵絲圍成一個正方形，正方形的邊長是多少？

(2)一臺計算機已使用1700h，預計每月再使用150h，經過多少月這臺計算機的使用時間達到規定的檢修時間2450h？

(3)某校女生占全體學生數的52%，比男生多80人,這個學校有多少學生[2]？

生13：設正方形的邊長為xcm，列方程為 4x=24.

生14：設x月后這臺計算機的使用時間達到2450h，那么在x月里這臺計算機使用了150xh.列方程為1700+15x=2450.

生15：設這個學校的學生數為x,那么女生數為0.52x, 男生數為(1-0.52)x.列方程為0.52x-(1-0.52)x=80.

師：觀察上面的例題，列出的三個方程有什么特征？

生16：只含有一個未知數x，未知數x的指數都是1，等號兩邊都是整式.

師：只含有一個未知數(元)，未知數的次數都是1，等號兩邊都是整式，這樣的方程叫做一元一次方程.

設計意圖通過探究例題，讓學生熟練“尋找相等關系→設未知數→列出方程”的解題步驟，培養了學生的觀察能力、歸納能力和分析問題、解決問題能力以及直觀想象等數學核心素養.

1.3 鞏固拓展訓練

師：(1)下列式子哪些是方程，哪些是一元一次方程？

①x=1，②3x+2=x-7，③-a+3>0，

④-3x+1.8=3y，⑤x2+2x-6=0.

(2)根據下列問題，設未知數，列出方程，并指出是不是一元一次方程：

①環形跑道一周長400m，沿跑道跑多少周，可以跑3 000m？

②甲種鉛筆每支0.3 元，乙種鉛筆每支0.6元，用9元錢買了兩種鉛筆共20支，兩種鉛筆各買了多少支？

③一個梯形的下底比上底多2cm，高是5cm，面積是40cm2，求上底．

④用買10個大水杯的錢，可以買15 個小水杯，大水杯比小水杯的單價多5 元，兩種水杯的單價各是多少元？

設計意圖使學生對于方程與一元一次方程的概念的認識，以及列方程的基本步驟得到鞏固，在教給學生數學知識的過程中，滲透了數學模型的思想方法，培養學生的思維品質和應用意識以及數學建模等數學核心素養.

2 教學反思

2.1 聚焦核心概念

概念教學是初中數學課堂教學中最重要的成分，而生成數學概念的過程是典型的數學抽象的過程.本節課的主要內容是方程及一元一次方程的概念，根據問題中的數量關系設未知數建立方程模型.在實際教學中，教師通過設計不同的問題情境，引導學生進行感知、抽象和歸納，概括出這類方程和一元一次方程的屬性，有利于加深學生對于方程及一元一次方程概念的深層理解.教師有意識地按“尋找相等關系→設未知數→列出方程”的步驟組織學生進行探究，滲透數學核心素養，激發學生的學習興趣，萌發學生的求知欲望，培養學生由實際問題抽象出數學模型的能力.

2.2 關注核心理念

《義務教育數學課程標準(2011年版)》指出：數學教學活動應激發學生興趣，調動學生積極性，引發學生的數學思考，鼓勵學生的創造性思維；另外，要注重培養學生良好的數學學習習慣，使學生掌握恰當的數學學習方法.本節課的教學難點是從列算式到列方程的思維習慣的轉變.在小學，學生習慣于采用算術方法來解決問題，而對于如何設未知數，如何尋找等量關系，如何用含有字母的式子表示相等關系，雖然也有所接觸，但明顯不夠熟悉，從算術方法過渡到代數方法的思維轉變存在一定的困難.因此，本節課在實際教學時首先設置了兩個問題情境，引導學生分別用列算式和列方程的方法來解決，讓學生比較算術方法和方程方法的區別，使他們在解決問題的過程中體會到列方程解應用題的優越性，從而更加重視方程的學習，進而培養了學生的數學核心素養，更實現了他們的核心思維理念的轉變.

2.3 培養核心素養

將實際問題中的數量關系用方程形式表示出來，就是建立一種數學模型，這種建模思想在本章中占主導地位.本節課緊緊圍繞“數學核心素養”展開教學，教師出示問題串，讓學生設未知數、列出方程，一方面是要分散列方程這一教學難點，化整為零地培養由實際問題抽象出方程模型的能力，另一方面是通過一些具體的方程歸納出一元一次方程的概念，培養學生的數學運算、數學抽象、數學建模等核心素養以及創新意識.學生在分組討論、合作交流過程中，體驗到方程是刻畫現實世界的有效模型，初步感受到用方程解決實際問題較以前的方法更簡單，并且還是一種通用的方法與手段，從而在感悟中使他們發現問題、分析問題和解決問題的能力得到升華，數學核心素養也得到全方位培養.

數學核心素養的培養是使學生得到全面發展的關鍵一步，作為一線數學老師，更要注重提升自身的數學素養，進一步學習數學核心素養的相關理論知識，轉變教學理念，切實將培育學生核心素養融入到每一節課的教學環節中，從而實現學生的全面發展.