尋找“隱含條件”，理清解題思路

劉新春

許多數學問題常常因為發現不了隱含條件而無法求解或方法繁復，耗時太多．如能將題目中的各個條件用幾何化、圖表化、代數化、模式化、結論化的形式相互轉化，往往能發現隱含條件，找到解題思路．下面以解析幾何問題為例說明如何發現隱含條件．

一、數形結合，巧妙轉化

例1已知直線l1：ax-by+4=0與直線l2：（a-1）x+y+b=0平行，且原點到兩直線的距離相等，求實數a，b的值．

分析本題中有兩個條件，條件（1）：兩直線l1與l2平行；條件（2）：原點到兩直線的距離相等．如能將兩個條件直接轉化為關于a，b的兩個方程（數量表征），即可求出a，b的值．但如何轉化、表示為二元方程，因轉化策略和方法不同，難易差異很大．

條件（1）即

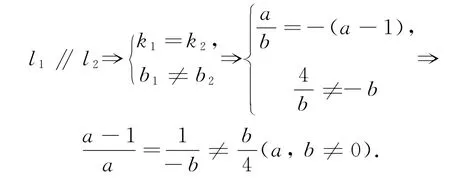
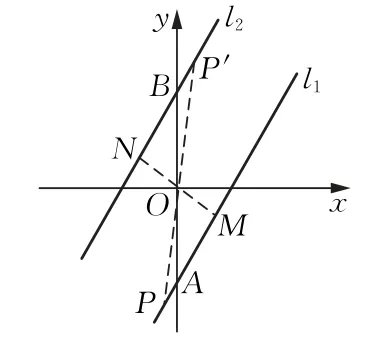
圖1

條件（2）即OM=ON．直接應用可得到如下解法：

簡解由l1∥l2可得：

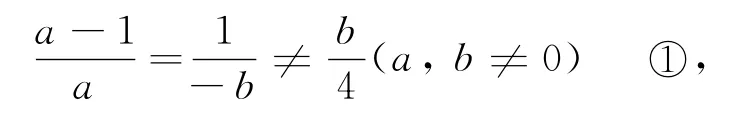
又因為原點到兩直線的距離相等，可得：

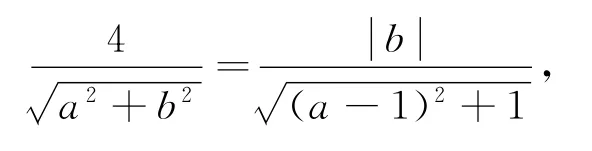
化簡得16（a-1）2+16=b2（a2+b2）②．

上述解法中，OM=ON是最容易想到的直接條件，但也是形式最繁的數量關系式，求解a，b的值非常煩瑣；若結合圖形可知：O點到兩直線的距離相等即兩直線關于原點對稱，這是隱藏在條件OM=ON后的隱含條件，而OA=OB是隱含條件“兩直線關于原點對稱”的直接推論，即為（b≠0），簡潔明了，立即可求得b=±2．

比較上述兩種解法可知，只有抓住題目中兩個條件的本質屬性——幾何特征——兩直線關于原點對稱這一隱含條件，并用最簡單的數量關系表示，才能快捷地獲得簡單的解題方法和簡明的解題過程．

二、變換圖形，發現性質

例2在平面直角坐標系xOy中，點B與點A（-1，1）關于原點O對稱，P是動點，且直線AP與BP的斜率之積等于．

（1）求動點P的軌跡方程；

（2）設直線AP與BP分別與直線x=3交于點M與點N，問：是否存在點P使得△PAB與△PMN的面積相等？若存在，求出點P的坐標；若不存在，說明理由．

分析（1）（x2+3y2=4且x≠±1）；（2）此題的關鍵是如何表征“△PAB與△PMN的面積相等”這一條件．

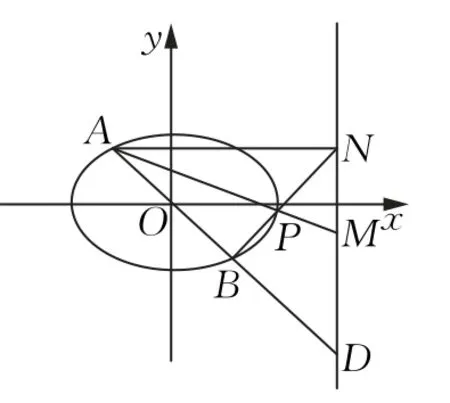
圖2

?PA·PB=PM·PN

?（xA-xP）（xB-xP）=（xMxP）（xN-xP）

?xP=．

表 征（4）S△APB=S△PMN?S△ADM=S△BDN=S△ABN=S△AMN

?M是DN中點，P是△ADN的重心

在上述幾種表征形式中，表征（1）抓住圖形中三角形的邊的特征給出數量關系，最接近題中原始條件，也最容易想到，但計算M，N兩點的縱坐標步驟較繁，運算過程也非常復雜；表征（2）抓住了∠APB=∠MPN這一條件，從角的特征出發，把面積相等表征為三角形邊長的乘積關系，再運用線段在同一條直線上的射影的比值相等，因而思路巧，方法簡，運算少；表征（3）與表征（1）類似；表征（4）抓住圖形的整體特征，充分運用B點是AD的中點條件，從兩個三角形的面積相等關系挖掘出P點為△ADN的重心這一隱含條件，題目中條件的本質屬性更加凸顯．

三、特殊引路，直覺猜想

例3如圖，在平面直角坐標系xOy中，已知圓O：x2+y2=4，F（0，2），點A，B是圓O上的動點，且FA·FB=4，是否存在與動直線AB恒相切的定圓？若存在，求出該圓的方程；若不存在，請說明理由．

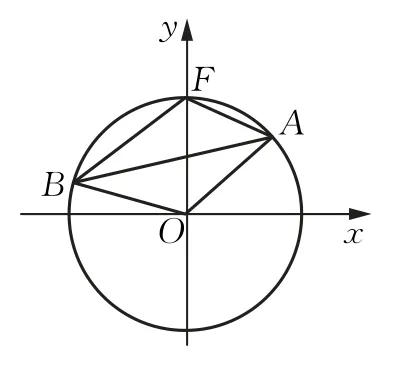
圖3

分析直覺告訴我們，若定圓存在，應與圓心O或定點F有關．因為A，B是動點，若取FA=1，FB=4，可知∠FAB=90°．點F到AB的距離為1，點O到AB的距離為（中位線）．再令FA=FB=2，可算得點F和點O到AB的距離均為1．合情猜想，點F到AB的距離為定值1．換句話說，AB與以點F為圓心，1為半徑的圓相切．這就是本題中的核心隱含條件．如何證明？聯想FA·FB=4、三角形的面積公式、余弦定理等條件可得以下證明：

作FH⊥AB于點H，連結OA，OB．設△ABF的面積為S，

在△OAB中，由平面幾何知識可知∠AOB=2π-2∠AFB．

由余弦定理得

AB2=OA2+OB2-2OA·OB·cos∠AOB=4+4-2×2×2cos2∠AFB=16sin2∠AFB．

與（*）聯立可得FH=1．

從而所求定圓的方程即為x2+（y-2）2=1．

本題的求解思路其關鍵是通過直覺判斷、特殊引路、合情猜想、推理論證等環節發現并證明隱含條件“定點到直線的距離為定值1”．可從上述探究過程中體會如何探索幾何圖形的本質特征．

四、抓住“有界”，化隱為顯

例4如圖，在平面直角坐標系xOy中，已知以M為圓心的圓M：x2+y2-12x-14y+60=0及其上一點A（2，4），

（1）（2）略．

（3）設點T（t，0）滿足：存在圓M上的兩點P和Q，使得求實數t的取值范圍．

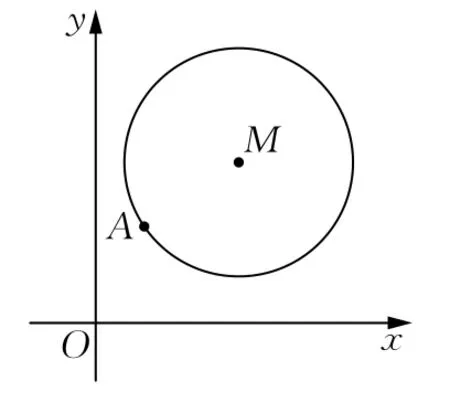
圖4

分析實數t滿足什么樣的數量關系，本試題的已知條件中沒有直接給出，但從向量關系中不難發現：，P，Q是圓上兩點，其長度不超過直徑，即從而發現了本題中的關鍵隱含條件．

即（t-2）2+（0-4）2≤100，解得t∈．

在求解解析幾何問題時，經常會運用圖形特征中的限制條件，如圓上兩點的距離范圍，橢圓、雙曲線、拋物線上點的坐標的限制條件，求離心率或其他參數的范圍等問題．解析幾何問題中的隱含條件首先是圖形中隱含的幾何特征，抓住最本質的幾何特征，就能發現隱含條件．其次是尋找同一個幾何特征的不同數量關系，有些是顯而易見的，有些是深藏不露的，需要我們去發現．