“雪花”曲線漫談

張志勇

美麗的分形是大自然景物的抽象，它無比豐富的細節、絢麗多彩的結構常令我們流連忘返，圖1中的科赫（Koch）雪花曲線給我們以美的遐想．分形在多個領域有著廣泛的應用，如物理中的湍流、化學中的高分子鏈、天文學中的星團分布、地理學中的河流與水系、生物學中的全息現象……

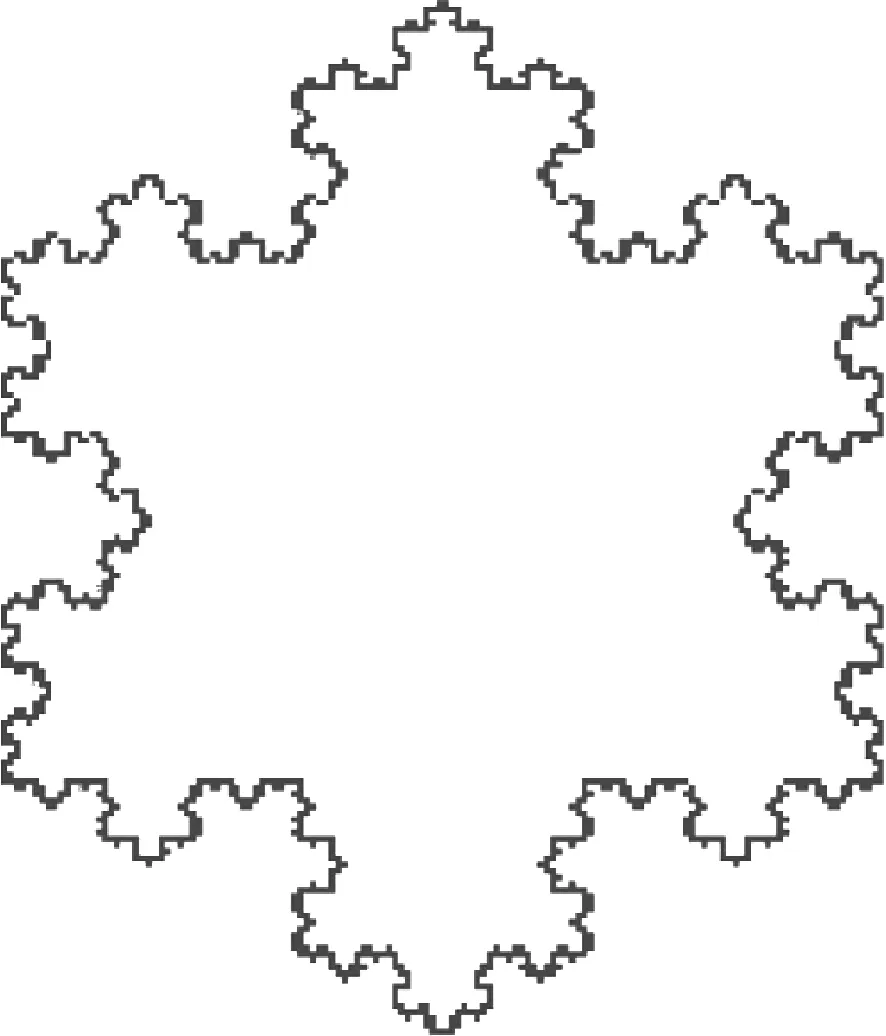
圖1

下面我們要探究的是美麗的分形背后的數學身影．

首先，我們來了解一點分形的科普小知識．提及分形，首先要涉及的是其自相似性，所謂自相似性即是指局部是整體成比例縮小的性質．通俗一點，就是當用不同倍數的照相機拍攝研究對象時，無論放大倍數如何改變，看到的照片都是相似的．由此，你能想象科赫雪花曲線的自相似性嗎？

圖2

雪花曲線由瑞典數學家科赫于1904年構造，因為酷似雪花，所以叫“雪花曲線”．其構造規律是這樣的：從圖4-1所示的等邊三角形開始（稱為初始元），將三角形的每條邊三等分，并在每條邊三分后的中段向外作新的等邊三角形（舍去中間的一段，保留兩側的兩段，將中間的一段改成夾角為60°的兩個等長的直線段，如圖4-2），再細分便得到圖4-3……不斷重復這樣的過程，隱去不要的部分，便可得到圖1所示的雪花曲線．

圖3

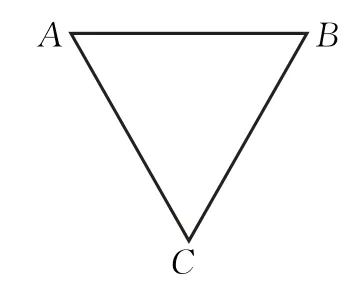
圖4-1

圖4-2

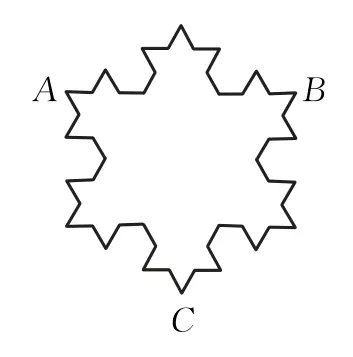
圖4-3

從圖形的構造過程不難理解雪花曲線的自相似性．其實在我們的教材《必修5》數列單元習題中，就有雪花曲線的構造．

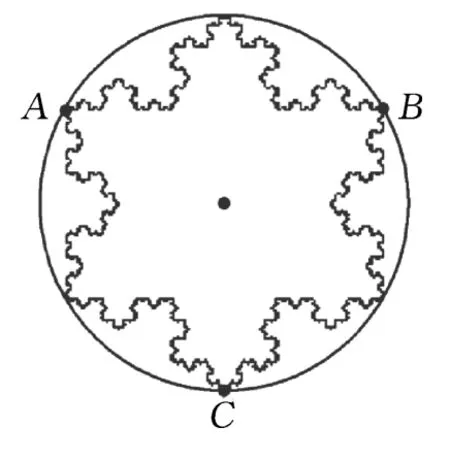
圖5

雪花曲線的奧妙不僅在于它的自相似性，我們作出初始三角形的外接圓（如圖5），可以發現雪花曲線永遠不會超出這個圓，也就是說雪花曲線圍成的面積是有限的，如果再告訴你，雪花曲線的周長卻是無限長的，也就是說用一個無限長的圖形圍成一個有限的面積，是不是有點“難以置信”！

下面，我們用數列知識來證明這個結論．

我們設初始三角形ABC的邊長為a，經過n次生長后，得到的小三角形的邊長為邊數En=3·4n，面積為，這樣n次生長后總的周長之和為而所圍成的面積之和，這樣生長無限次后，邊長和即周長趨于無窮，而面積和則趨于定值．當然，要說明的是，這個令人驚異的結論，面積的有限性，要用到一丁點兒極限的知識，但是我們可以這樣想，在一張紙上畫雪花曲線，不管生長多少次，它都不會超過一張紙的，顯然它的面積是有限的．

最后我還想告訴同學們的是，雪花曲線的神奇之處不僅如此，其身上還有很多不為人知的奧妙之處，如曲線上有許多折點，到處都是“尖端”；曲線雖然連續，但雪花曲線沒有切線．

透過雪花曲線，我們可以深刻感受到：分形幾何，不愧為“真正描述大自然的幾何學”．它如此貼近我們的生活，不僅有外在之美，其內在深奧的數學之美更需要我們用數學的眼光去積極探索，隨著我們學習的深入，或許會揭開其中更多的神秘面紗．

圖6