冪級數在函數領域的應用

趙青波

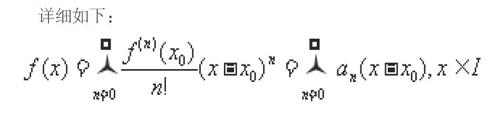
摘要：冪級數是數學領域中的一種基礎知識，同時也是數學計算中的一種重要“工具”，其在函數領域中有著較為廣泛的應用，如在復變函數等領域中。冪級數在函數領域中的應用決定了其在函數計算等過程中的重要性，一般來說，運用冪級數求函數的高階導數、求數值級數的和、應用在近似計算中、應用在微分方程的解法、。在數學解題過程中，通過把握冪級數在函數應用中的關鍵點，也能夠起到事半功倍的作用，本論文通過分析冪級數在函數中具體應用的基礎上，闡述冪級數在函數中應用的關鍵點，以此來多方位的展示出冪級數的在函數中的應用。

關鍵詞：冪級數;函數;應用

引言冪級數在函數中的應用是數學計算中解決函數問題的一種有效思路，同時也能夠為函數類型題的計算提供一種“捷徑”，通過對冪級數的性質進行分析，能夠觀察到，冪級數與函數之間存在著關聯性，這也是冪級數作為函數解題“工具”的基礎。如冪級數是函數函數項級數中最基本的一類，在冪級數的收斂域上與函數之間存在的明確的關聯性，在收斂域上函數項級數的和是x的函數，稱為函數項級數的和函數。本文通過對冪級數概念與性質的闡述，結合具體的解題思路，對冪級數與函數的應用進行分析。

一、冪級數概述

冪級數是指在級數的每一項均為與級數項序號n相對應的以常數倍的（x-a）的n次方（n是從0開始計數的整數，a為常數）。以冪級數常見的三個性質為例，以下進行闡述。

1.∑ an xn 在 | x | < R 內絕對收斂，在 | x | > R內 發 散，其 中 R 稱? n=a 為收 斂半 徑，此時再根據Hadamard 公式進行相應計算。

2.如果函數S（x）是收斂域（-a，a）上的連續函數，則S（x）在x=a左連續。

3.在收斂半徑（-a，a）的范圍內，冪級數可以任意次逐項求導或者求和，并且產生的新的冪級數的收斂半徑不變。

二、冪級數在函數中的具體應用

（一）利用冪級數求函數的高階導數

在常規數學計算中，將冪級數運用到求函數的高階導數中，不僅能夠降低計算的復雜性，也能夠提高計算結果的準確性。以下，本論文將這種應用分為三步進行闡述。

首先，需要使用冪級數展開的方法，并將其展開到指定點處的冪級數，這是應用的前提。其次，計算冪級數展開式的收斂域，這直接關系著后面的計算。

最后，需要使用泰勒級數的理念進行冪級數的計算，即一個函數在指定點處的冪級數展開式，具有唯一性，冪級數相等情況下，x-x0次數相同的項，其系數也是相等的。

詳細如下：

（二）利用冪級數求數值級數的和

在數值級數的和的計算的過程中，冪級數也有著自身的應用性，在該計算中，應用冪級數往往能夠提高計算的效率，以下，本論文將其具體分為三個步驟。

首先，需要將常值級數轉化為冪級數，把其中的n次方項轉化為xn，以此來構成冪級數，這是應用冪級數的前提條件。

其次，需要對構成的冪級數進行求解，將其收斂域與函數計算出來。

最后，借用冪級數的特性，冪級數收斂域中所組成的常值級數之和，與和函數在這個點中的函數值是相等的。

（三）冪級數在近似計算中的應用

根據冪級數的特性，在函數的冪級數收斂域中的點上，相應的函數值，其近似值可以用收斂域中的點的冪級數所對應的常值級數的部分和近似，這也可以保證預期的準確度。

冪級數應用在近似計算中，有著自身的前提，即函數要能夠展開成冪級數，如果能夠符合這個前提，則該應用就充分成立，符合以下推論：f（x）=a0+a1x+a2x2+a3x3+...+ahxh+...（-R

（四）微分方程的冪級數解法

f（ x） 的原函數不能用初等函數的有限形式表示出來時，計算 f（ x） 的定積分就遇到了困難，現在，可以利用冪級數取有限項的辦法近似計算這些定積分的值.我們在計算積分時，當具體要求被積函數能夠展成收斂的冪級數，且積分限必須在冪級數的收斂域之內，然后利用逐項積分來計算所求定積分的值。以下，本論文將這種應用分為四個步驟進行闡述：

首先，設微分方程的解函數為冪級數。

其次，解函數的冪級數表達式代入微分方程，化簡、合并等式兩端的同次項。

再次，比較等式兩端同次項的系數，得到所設冪級數的系數表達式。

最后，對于得到的冪級數，能夠求出和函數的，則和函數即為微分方程解的初等函數表達式;對于無法用初等函數描述的冪級數，則可以用其部分和作為微分方程的近似解。

三、冪級數在函數應用中的關鍵

（一）函數展開為冪級數的可能思路

常用的基本思想與方法為：借助級數的數乘、加減運算法則、逐項可導、逐項可積的微分性質，將函數變換成已知冪級數展開式及收斂域的函數描述形式，然后借助運算性質寫出冪級數. 該方法也稱為函數展開成冪級數的間接法. 另外也基于函數在指定點處冪級數的唯一性，通過待定系數的方法求冪級數的系數，從而得到最終的冪級數展開式。

（1） 所求函數→變換為容易寫出冪級數的函數加減乘形式→對函數執行加減、求導、求積→已有冪級數展開式的函數→對函數及冪級數進行逆運算→所求函數的冪級數。

（2） 已有冪級數的展開式的函數→函數求導、求積分及冪級數展開式逐項求導、求積分→所求函數的冪級數展開式。

（3） 直接求各階導數，借助泰勒級數公式直接寫出相應的冪級數表達式

一般來說，函數展開為冪級數有兩種思路，即直接展開法和間接展開法，以下進行詳述：

①直接展開法：