利用《幾何畫板》微課做數學實驗的功用性和價值性

福建省龍巖第一中學 張垣功

在教材中設置了大量數學動手實驗,主要是通過創造問題情境,認知現實生活，設計實驗模型等環節提出。然后，通過問題導入的實驗，以自身掌握的知識和經驗為基礎，主動地建構數學概念；通過觀察驗證的實驗，以教師啟發的互動和推理為手段，積極地發現數學定理；通過合情類比的實驗，以教材提供的例題和習題為母題，有效地拓展問題結論。本文就《幾何畫板》微課在數學實驗教學中的功用與價值等方面談一些看法。

一、利用《幾何畫板》微課做數學實驗有助于學生加深對概念的理解，對要領的掌握

在數學概念教學中，我們經常會受概念的引入和形成所困惑，對數學概念的本質屬性挖掘不到位，因某些數學概念抽象，往往是知其然而不知其所以然，為了讓學生能理解某數學概念的發生、形成和發展過程，真正理解概念的本質屬性，這就要求教師在課堂上講解概念時應根據學生已有的知識背景和活動經驗，展示一些操作、實驗、觀察活動，讓學生思考、交流、反思等過程。

如在講二面角的概念時（如圖1），可以用《幾何畫板》軟件做一個微課實驗：拖動點A，則點A所在的半平面也隨之轉動，即改變二面角的大小和位置，圖形的直觀變動讓學生觀察在各個不同位置時二面角的圖形特點，有利于幫助學生建立空間觀念和空間想象力，從而加深對概念的理解。

又比如在講橢圓的概念時，可以用《幾何畫板》微課畫2個定點F1，F2和線段AB的長為定值。然后在線段AB上取一點E，分別以F1為圓心，AE的長為半徑和以F2為圓心，BE的長為半徑作圓。讓學生猜測和探討兩圓的交點軌跡。學生各抒己見之后，老師拖動E點在線段AB上逐步雙向慢速移動的演示，也可以設置點E在線段AB上雙向慢速移動的一個動畫按鈕演示，學生豁然開朗：“原來是橢圓”，且其運動軌跡是逐步在不斷追蹤點E而形成的。接著老師用鼠標拖動點B（即改變線段AB的長），使得|AB|=|F1F2|時，滿足條件的點的軌跡變成了一條線段F1F2。當|AB|＜|F1F2|時，滿足條件的點的軌跡則不存在。通過上述實驗的演示與操作，問題情境的創設以及學生的討論回答，使學生對橢圓的概念會有一個清晰準確地認識和全面深刻的理解，不僅使他們知其然，更能知其所以然。

二、利用《幾何畫板》微課做數學實驗有助于學生發現數學原理、猜想數學結論

在數學定理教學中，如何合理講授和推出數學原理是經常茫然的課題，其教學方法大都是直接給出原理的內容，沒有注重知識原理的來龍去脈，對學生的思維形成產生不良的效應，同時，對原理的應用也浮在表面，甚至使學生一知半解，似懂非懂，造成感知與概括之間的思維斷層，學生只記著課本提供的公式、定理，然后簡單套用，完全處于一種被動地位，這就要求教師在課堂上充分利用多媒體手段把原理的發生和發展過程展示出來，并揭示原理形成的規律。

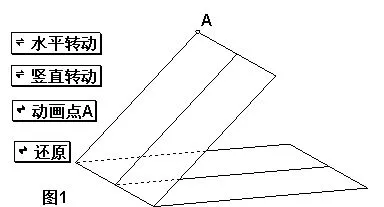
圖1

例如，在講解高中新課程必修4（人教版）第154頁的例4時，可以用《幾何畫板》軟件做一個微課：求已知圓的內接矩形的最大面積，即設置這樣的一個動畫：畫一個圓O，作任一半徑OA，在OA上取一點C，過點C作EF⊥OA交⊙O于點E，F，過點E，F分別作EH∥OA，FG∥OA交⊙O于G、H。連接G、H。接著使點C在線段OA上雙向慢速運動，觀察圓O內接矩形EFGH的面積的度量值，發現點C在線段OA上運動過程中，矩形EFGH的面積值是先增后減。反復演示，并請同學們注意，面積取最大值時，此矩形會有何特征？先猜想、討論，后顯示EF和GF的度量值，得到結果是正方形，再從理論上加以證明。這樣，學生就能主動地在輕松又活躍的課堂氣氛中猜想數學結論，再根據這個結論設置相應的動畫按鈕（如圖2和圖3），通過變換不同的位置，得到相同或不同的數量關系，從而推出相應的結論。用同樣的手段和方法對多面體、旋轉體的截面面積進行探索就能發現其統一的內在原理。

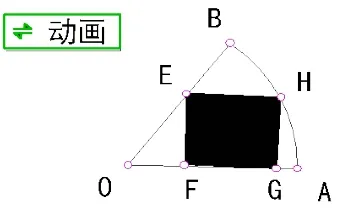
圖2

圖3

三、利用《幾何畫板》微課做數學實驗有助于學生探究數學規律、驗證數學知識正確與否

在數學探究教學中，恰當改變、增減數學試題的條件或結論，讓學生體會數學問題的精彩，體驗學習數學的樂趣，積極主動學習有價值的數學，也是值得教師思考的話題，因此在教學中，教師努力創設《幾何畫板》微課，根據學生的實際認知水平及課程標準，對教學知識進行整合、重組、補充、加工，使學生能感受數學應用的實際意義，構建課堂的有效性。

如線性規劃教學中求目標函數的最值，可以利用幾何畫板的移動、旋轉、測算功能，使與目標函數所在直線平行的直線在任何一個位置，一邊移動（轉動），一邊測算其值。觀察最值的位置，確定最優解。如圖4點擊，移動按鈕，畫面將出現一組平行直線（一束直線）和相應的數值（如圖4）。

圖4

四、利用《幾何畫板》微課做數學實驗有助于學生找到解決問題的有效途徑，拓展數學問題的結論

數學結論與求解過程是教學過程中一對十分重要的關系。展示教學過程能喚起探索與創造的歡樂，激發認知興趣和學習動機；展現思路和方法，教人怎樣學習，它能幫助我們提高學生的創新能力。利用《幾何畫板》進行數學實驗教學是一種讓學生經歷知識探索過程，發現新認識、新信息，提出新問題、解決新問題的創造性學習。因此，在數學課堂教學中，發現學生解題時因為找不到突破口而困惑，可以引導學生通過數學實驗來發現規律，從而獲得解題的多種途徑。

圖5

又如：設M（x1，y1）為橢圓x2+2y2=2上的任意一點，過點M作一條斜率為的直線l，又設d為原點至直線l的距離，r1，r2分別為點M到橢圓兩焦點的距離。試證明：常數。其解答可用代數方法順利解決，此題若作深入分析，引入《幾何畫板》輔助教學（如圖6），必讓學生學有所得。

探索：“測算”MF1和MF2與直線l所成角的大小并列展示在平臺上，提示學生注意兩角關系，當點M再次運動時，發現這兩角保持相等。說明MF1和MF2存在反射關系。可方便進行實驗：過M作直線l的垂線（法線），并標記鏡面，構造點F1關于的對稱點，結果看到點在射線AF2上。

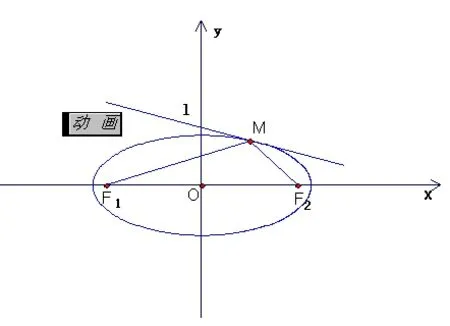
圖6

再探索：例題中橢圓x2+2y2=2改為雙曲線x2-2y2=2，結論還會成立嗎？重復以上操作，學生驚奇地發現結論是如此相似，直線l還是雙曲線的切線，依然是定值。

總之，使用《幾何畫板》微課做數學實驗教學，通過具體的感性的信息呈現，能給學生留下更為深刻的印象，使學生不是把數學作為單純的知識去理解它，而是更有真實感地去把握它。這樣，既能激發學生的情感、培養學生的興趣，又能大大提高課堂效率。