享受學習過程 提高自身素養

☉云南省曲靖市會澤實驗高中 許德福

不管是對數學教學進行的研究，還是對學生整體素質培養的研究，其整體的研究對象都是指向學生的.但是在實際的教學過程中，教師往往會忽略學生的學習情況，將重點放在自己的教學過程中.但教學的行為主體與學習的行為主體是不相同的，所以，從提高教學有效性的角度出發，顯然教師研究學生的學習過程更加的有意義.這會將教學的主體從原先的教師轉移到學生身上.在這個過程中，教師能夠體會到學生進行學習的具體過程，而在這個過程中發現的一些問題是理論難以解決的.這對于教師的教學有一定的挑戰，這就需要教師能夠提高自身的專業素養.

在進行函數的相關概念的學習過程中，教師對函數的講解從相關的模型引入，對函數的定義是使用法則來進行的.但是這與學生之前認知的函數不同，學生是通過例子來對函數進行理解的，這是學生在學習函數過程中的一種必然的現象.［1］這是由于在學習過程中對函數的練習是通過習題的方式來進行的.這些習題正好為學生函數的學習提供了例子.

但是，我們不能就此認為學生對函數是一無所知的.但能看做學生對函數的理解是維持在最基本的層面上，不是真正的理解了函數的本質內涵.所以對于函數概念的理解應當是從定義入手，如在講解時要先讓學生理解函數的三要素：定義域、值域、對應關系（對應法則），如圖1所示.

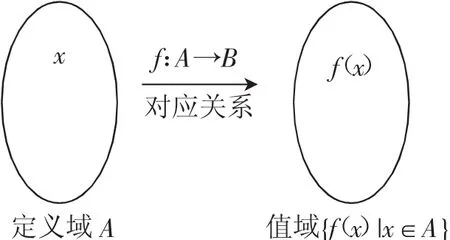
圖1

對于函數習題以及例子的選擇也應當從這個定義入手，這樣才能夠做到真正理解函數概念，并能夠進行相關的練習.

例1已知函數若f（x）=10，則x=______.

例題答案：由題意可得f（x）=x2+1=10，且x≤0，得x=-3.

例2已知函數f（x）的定義域是（0，+∞），且滿足f（xy）=f（x）+f（y），，如果對于0＜x＜y，都有（fx）＞f（y），

（1）求f（1）；

（2）解不等式f（-x）+f（3-x）≥-2.

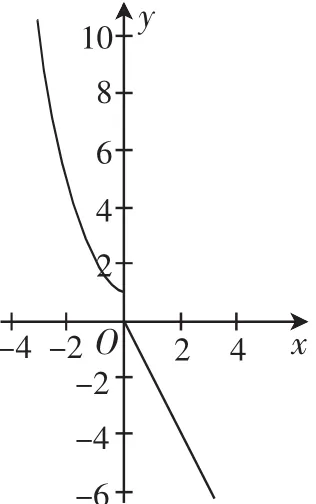
圖2

答案解析：（1）令x=y=1，則f（1）=f（1）+f（1）?f（1）=0.

因為f（x）的定義域是（0，+∞），且對于0＜x＜y，都有f（x）＞f（y）可知，f（x）為減函數，解得-1≤x＜0.

一、讓學生理解函數

對于函數的教學，若讓學生從概念上進行理解并不是一件容易的事情.在高中數學知識學習中，函數的概念比較難以理解及掌握，并且，很多知識點的學習也需要建立在函數概念學習的基礎上來進行.

在剛開始進行函數知識學習的時候，學生對于函數的理解是在集合這一概念之上進行的.在進行學習之前，學生對于對應法則的接觸并不多，在進行函數建立的時候才對這一概念有了接觸與了解.在此之后，對于函數的學習是建立在學生對于函數的理解之上進行的，讓學生能夠從不同的角度來認識函數，并了解函數的真正用途.這就需要學生首先從細節方面認識函數，之后，在學生接觸不同函數的過程中讓學生對函數進行整體的了解.尤其是了解函數的具體概念，這是在教學過程中非常容易被忽視的內容［2］.在進行教學的過程中，需要對知識特別是定義與概念進行“反思”.這是一個重要的步驟，能夠使學生在具體的定義之中了解函數的基本性質以及對函數進行深化的理解［3］.

例3圖3中（1）（2）（3）（4）四個圖像各表示兩個x，y的對應關系，其中y是x的函數關系的有______.

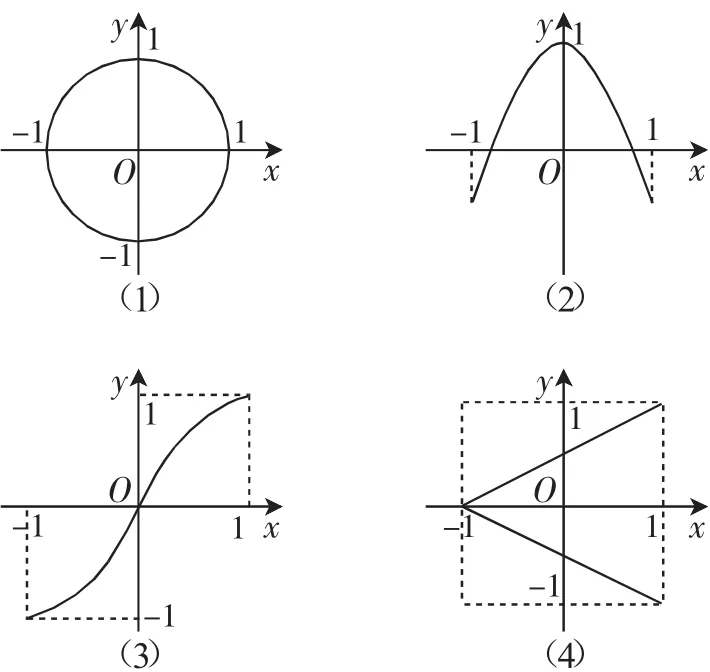
例題解析：由函數定義可知，任意作一條直線x=a，則與函數圖像至多有一個交點.根據本題的問題來說，當-1≤a≤1時，直線x=a與函數的圖像只需有一個交點，當a＞1或a＜-1時，直線x=a與函數的圖像無交點；從圖像來看，符合此條件且表示y是x的函數關系的有（2）（3）.

用這道鞏固習題就可以讓學生直觀的反思函數最基本的定義概念：如果對于x在某一范圍內的每一個確定的值，y都有唯一確定的值與其對應.所以說，對函數的理解應當建立在理解了定義的基礎之上來進行，從集合以及對應法則方面來進行理解，更能夠抓住函數概念的根本所在.

二、教師如何引導學生學習

首先，需要對函數最初的概念構建進行重視以及了解.函數的概念是高中知識體系中最為基礎的部分，這也正是很多的教師以及學生在學習的過程中常常忽視的地方.再加上與函數概念相關的練習題比較少，平時在學習過程中又不注意這方面的練習.因此在進行數學學習的過程中，要更加的關注對函數概念的理解，從根本上重視函數的學習.

第二，重視具體函數對函數概念的反哺.在對函數的具體概念進行了解之后，需要通過多種不同的函數，來對函數的概念進行驗證.在這個過程中，學生對于函數的理解會更加的深刻，這個過程也是學生思維鍛煉的過程.

第三，在綜合情境當中對函數的定義進行創新應用.在近幾年的高考試卷當中，特別重視將情境與題目進行結合的考察，所以學生在學習函數的過程中要將函數知識與實際生活聯系起來進行學習.

三、在關注學習中研究教學

對于學生學習情況的掌握以及學習難點的了解是一個教師必備的素養.特別是在進行高中數學的教學過程中，對于學生邏輯思維的培養以及推理能力的培養是非常有必要的.函數是在進行該種數學學習過程中的核心要點，教師如果能夠將函數的定義以及概念講解清楚，那么學生在之后對函數的學習過程將會變得非常的容易.作為高中數學最核心的內容之一，教師在教學過程中需要對學生的學習細節加以關注了解，從而找到學生學習的一些規律，這對于教師了解學生的學習過程有很大的幫助，有利于教師有針對性的進行課程的教學.

從整體上來講，在關注學生學習的過程中對數學教學進行研究，能夠提升教學的質量，可以看做是能夠掌握學生的學習過程，并且能夠提高自身專業素養的有效途徑.只有這樣，才能夠真正的了解教學的真諦以及本質.