高中數學教學中圖示理論的應用

☉江蘇省張家港市樂余高級中學 趙 鈺

如果把一個具體的理論應用到高中數學的教學過程當中，就會發現理論學習與實踐之間能夠有很好的關聯性.圖示理論在對很多學習理論的解釋上有非常重要的作用，特別是在數學的教學當中，圖示理論在幫助數學定理的理解、概念的把握以及問題的分析方面都有重要的作用.它能夠使教師對學生的知識掌握情況更加的了解.數學教師一直都非常地重視將圖示理論應用到高中數學教學的過程當中.圖示理論的應用在進行課程改革的過程中一直沒有進行過很大的改變，仍保持著其原有的色彩.

一、圖示理論的概念

圖示這一概念的發展有一定的歷史過程，大部分人將圖示理解為在腦海中已經形成的固有的知識結構，但是有一些人認為圖示是固有的認知結構（與上述所說的知識結構不同），還有一部分人對于圖示的理解是：圖示不是知識結構，而是對經驗的組合.雖然這些理解存在一些偏差，但是這些對于圖示的理解仍有相似之處，就是圖示可以視為在腦海中對已經具備的經驗或者知識的組合［1］.

著名的心理學家皮亞杰對圖示的探索非常的深入，所以通常會將皮亞杰理論叫做圖示理論.在這一理論當中，學習的發生是以圖示為基礎的，學習的過程主要是由順應、圖示、同化以及平衡四個部分組成的.

在進行課程改革之后，有爭議的部分就是理論支柱方面，但是在教學的過程中，構建主義還是具有很大的應用.構建主義對于學生原先積累的知識以及經驗有著較高的要求，這一點與圖示理論非常相似，所以很多學者認為構建主義可以看成圖示理論的一種發展，也可以看成一種重要的學習方式.

二、圖示理論在數學教學中的應用

圖示理論在教學過程中有著廣泛的應用，比如，在進行數學概念的學習過程中，學生能夠憑借原先的經驗來對概念進行理解［2］.

以蘇教版高中數學選修1-1中第二章“圓錐曲線”這一概念的學習為例，在進行學習認識之前，老師首先要講解圓錐曲線的由來：用一個平面采取不同的方式去截一個圓錐，就會得到不同的曲線，因此就產生了雙曲線、橢圓以及拋物線的概念.在實際的教學過程中可以發現，雖然在此之前學生在生活中會對這些概念有一定的了解，但是之前的這些圖示在現在學習數學知識的時候不能夠有效地促進數學的學習，因為這三種曲線的形成，都是需要通過兩個定點，或者一個點以及一條直線之間的關系來定義，而這種方法比較難理解［3］.比如，學生之前對于拋物線的理解就是一個物體拋出去形成的軌跡，但是如果將拋物線定義為到一個定點和一條直線的距離相等的點的軌跡，那么對于學生的理解來講就比較的困難了，這就是概念建構的復雜性.

在運用圖示理論進行學習時可以分成以下幾個步驟：

首先，讓學生自己羅列出對于橢圓以及雙曲線的知識的理解.這種做法可以讓圖示更加地清晰.第二步，利用計算機技術采用動畫表現的方式將平面與圓錐進行相切.

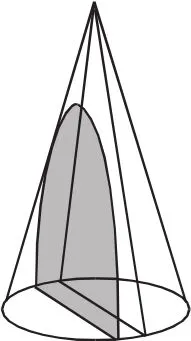
圖1

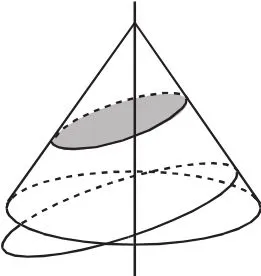
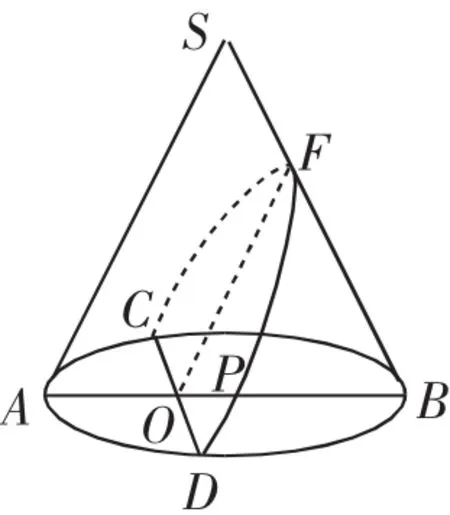
當截面位置平行于圓錐軸線時，所成截交線就是雙曲線，如圖1所示；當截面位置傾斜于圓錐軸線時，所成截交線就是橢圓，如圖2所示；當截面位置平行于圓錐一條母線時，所成截交線就是拋物線，如圖3所示；在演示之后進行總結歸納，這個環節可以讓學生以小組形式自行歸納.

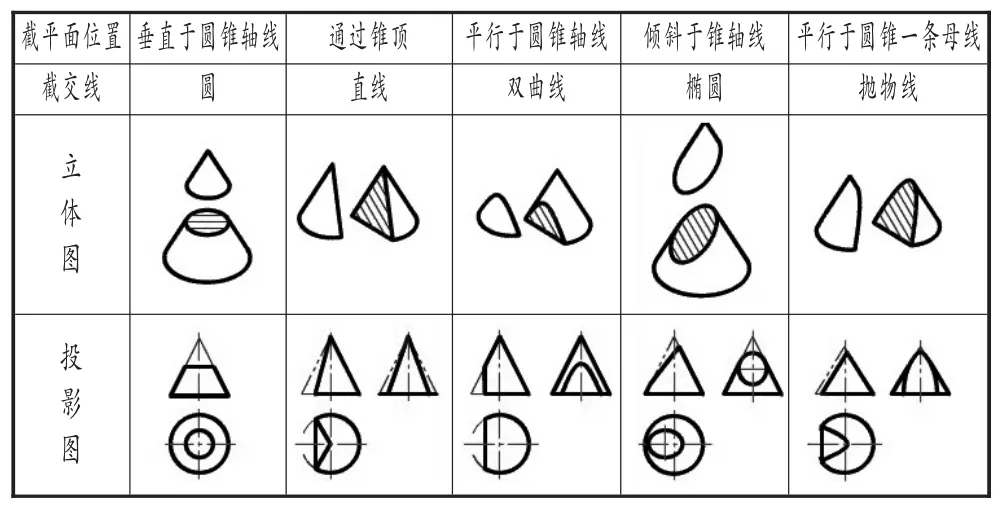
第三步，利用直線與定點之間的距離條件，對這三種曲線的概念進行重新理解.最后，對這兩種認識方法以及方式進行對比比較，建立新的圖示.

在高中數學教學的過程中存在的另一個重要內容就是對于問題的解決，根據圖示理論來看，學生要會運用自己已經建立起來的圖示去解決新的問題.在進行數學習題的練習過程中，一些習題是具有生活背景的，那么，對于學生的圖示是一個考驗的過程.因此教師在進行鞏固復習的時候，需多應用與生活息息相關的例題，來鍛煉學生運用圖示解決實際問題的能力.

例1根據我國汽車制造的現實情況，一般卡車高3m，寬1.6m.現要設計橫斷面為拋物線型的雙向二車道的公路隧道，為保障雙向行駛安全，交通管理規定汽車進入隧道后必須保持距中線0.4m的距離行駛.已知拱口AB寬恰好是拱高OC的4倍，若拱寬為am，求能使卡車安全通過時a的最小正整數值.

解：如圖4所示，以拱口AB所在直線為x軸，以拱高OC所在直線為y軸建立直角坐標系.由題意可得拋物線的方程為

取x=1.6+0.4=2，代入拋物線方程得

由題可知，y>3，即

又因為a>0，所以a2-12a-16>0，解得

又因為a為正整數，所以a應取14，15，16…

所以使卡車安全通過時a的最小正整數為14.

反思：本題的解題過程可歸納為兩步：①根據實際問題的意義，確定解題途徑，得到距拱口中點2m處y的值；②通過解不等式y＞3，結合問題的實際意義和要求得到a的值，值得注意的是這種思路在與最佳方案有關的應用題中經常用到.

三、高中數學教學中圖示理論的重要性

雖然在教學過程中運用圖示理論對高中數學的學習進行輔助不是一個創新之處，但是卻給人們帶來了很多反思.很多人認為高中數學的學習只是為了應付考試，所以在進行數學的學習過程中將自己困在應付考試的空間里面.雖然在這一方面會帶給老師很多職業成就.但是，如果從對數學的學習角度進行思考，就會發現自己并沒有理解數學學習的本質，沒有對數學學習的目的進行深入的了解.而對于數學的教學過程來講，這是一個教師自身能力以及專業素養提升的過程.但是如果只是為了應付考試，教師只會整天研究考試，沒有進行其他方面的研究鉆研，那么教師的教學能力以及專業素養沒有得到一定的成長.最后從數學對于學生成長的影響來講，雖然在現在對于數學知識的學習是為了能夠在高考當中取得好的成績，但是，數學學習的過程也是思維能力的鍛煉過程，學生能夠在數學學習過程中積累數學學習方法，并運用到實際生活當中，這對于學生的發展來講也是非常重要的.

上面所例示的這些思考，都是為了闡述一個道理，那就是圖示理論在教學過程中有著廣泛的應用.圖示理論在很多的教學過程以及相關的課程改革中都沒有進行較大的改動.圖示理論能夠直接將有效的學習過程展現出來，能夠幫助老師掌握學生的學習情況，提高老師的教學效率.