小學生的“算理”教學亟需加強

李志柏

摘 要：現在的數學運算評價已悄然轉向，命題不僅關注計算技能，更關注算理的理解，數學課堂教學不應滿足于學生會進行計算，還應注重“為什么這樣算”的“說算理”培養，應提供多種形式的練習題，讓學生進行運算并陳述算理練習，讓學生學會運算，學會分析，學會推導，學會思維，從而真正發展學生的運算能力。

關鍵詞：小學數學 算理教學 研究

在小學數學教學中，要會“算術”，更要會講“算理”，算法和算理是相輔相成的，培養學生的運算能力應當“法理并重”，會算法，懂算理，是運算能力的兩個重要組成部分，運算能力并非單一的，孤立的教學能力，所以，今后在進行相關計算教學時，要“法理”并重，加強“算理”的教學，以進一步提升學生的運算能力和對運算思維的培養。

一、不同的數學領域運算能力中需融會貫通的一些“算理”

1.整數四則運算，有時從低位算起，有時從高位算起

整數的加、減、乘三種運算在列豎式計算時，一般都是從低位算起。為什么不從高位算起呢？從高位算起行不行？整數的加減乘除是完全都可以從高位算起的。在數學的歷史發展過程中，在筆算形成的初期，確實都是從高位算起的，只是在整數的加、減、乘計算遇到進位時，因為需要改寫前面的數字，為了避免麻煩，才逐步演算進化為從低位起進行計算的。這個“算理”的前世今生，必須給學生講清楚，當然最好通過黑板演示，讓學生明白這個道理，才能讓學生對其心服口服，加深理解，在此基礎上，再進行推導演示，讓學生理解從低位算起的算理，通過實際扮演，逐步歸納出整數加、減、乘法的豎式計算法則，根據教材安排，依次進行課堂教學及演練，讓學生在熟悉算理，熟記法則的基礎上不斷練習，以達到熟能生巧的目標。

整數的除法，列豎式計算，則要從高位算起，除法豎式的格式本身和其他三種運算不太一致，這些外形的不同都源自除法本身的意義和豎式的要求。如果我們把乘法定義為一個數的連加，那么除法就是連減一個數了。豎式計算的實質，是將當前對于兩個數的計算歸納為它們各個數位上數的計算，以求出得數的各個數值上的數，要把計算的中間過程與最后的結果都記錄下來，除法的豎式發展到今天就是從高位算起了，那么高位除后余下的數退到低位繼續除，就影響原來低位上的商，自然增加了高位有余退位后再除的麻煩。所以整數除法求商，一般從高位算起，從高位到低位，依次求出商的每一位上的數，這樣既簡潔又方便。通過與學生共同探討，演示，歸納，總結，讓學生明白算理，在此基礎上，再推導出計算法則，則寓理于算，提高了學生的思維能力。

2.在小數四則運算中，數位有時要對齊，有時不要對齊

小數的加減法也和整數一樣，需要數位對齊，最顯著的標志就是小數點對齊，其算理也和整數一樣。但在小數的乘法里面，就不要數位對齊，而是末尾對齊就可以了。因為小數是基于十進制表示數量的需要而產生的，所以它的四則運算在很大程度上是仿照整數四則運算進行的，小數的乘法的基本算理也是與整數乘法的算理相通，例如：3.2×9在豎式計算時9要與2對齊，為什么呢？因為運用積的變化規律，3.2×9=0.1×（32×9）=0.1×288，既算出的結果是求288個0.1是多少，學生也就理解了9要與2對齊的意義了，小數乘小數也同理。比如：3.2×0.9=（0.1×0.1）×（32×9）=0.01×288，即求288個0.01是多少，學生也就慢慢理解了小數乘法豎式計算中為什么不是數位對齊，而是末尾對齊的意義了，算理也明白了。再通過不斷的訓練，反饋，再訓練，再反饋，在提高了運算能力的基礎上，也訓練了學生對算理的理性思維。

3.在分數四則運算中，有的要通分，有的卻不要通分

在分數的四則運算中，兩個分數相加減，必須先把計數單位化相同，即計算時先通分，計算時分母不變，只把分子相加減，這和整數加減法的算理是相通的，一致的。

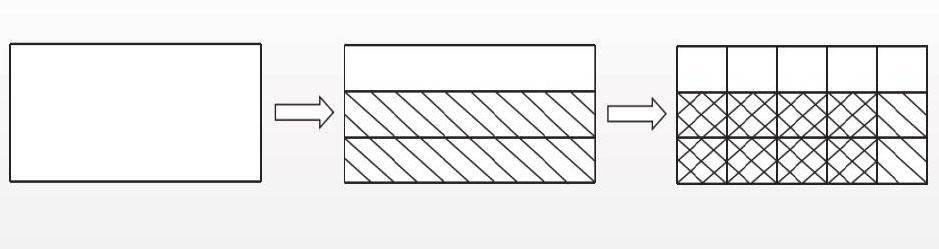
兩個分數相乘，用分子相乘的積做分子，用分母相乘的積作分母，這個法則，也可以看作分母單位化相同以后整數的運算。例如2/3×4/5的計算，可演化為2/3×4/5=（1/3×1/5） ×（2×4）=1/15×8即求8個1/15是多少，學生便明白了“兩個分數單位相乘”實質是在統一分數單位，用圖可演示如下：

分數除法的算理，可以理解的路勁較多，但它們的算理是相通的，咱們權且利用其中的一種，即把分數單位化相同，分母相同，就是分子相除，這就又轉化為分子的運算了，與前面的方法一致，也便于溝通理解。比如：3/5÷2/4=（3×4）/（5×4）÷（2×5）/（4×5）=（12/20）÷（10/20）=12÷10=1.2（小數）=6/5（分數），用字母表示即為：（a/b）÷（m/n）=（a×n）/（b×n）÷（b×m）/（b×n）=（a×n） ÷（b×m）=（a×n）/（b×m），在引導學生深入理解分數除法算理的基礎上，師生再共同推導出分數除法的計算法則，寓理于算，算中明理。

二、在計算教學中培養小學生“算理”思維的幾種做法

1.課堂上要讓學生多陳述算理，在數學課堂上，要讓每一個學生都有表達的機會，當眾矯正一個人的錯誤，其實受益一大批人，有時，甚至有必要給學生提供一個表述的框架，讓學生來表述，說算理練習是數學理解和語言表達的綜合體現。

2.抓住學生出現錯誤的有利時機，及時組織學生進行辨析、明理、幫學生矯正，疏通，在多次練習基礎上，以達到鞏固加強的效果。

3.改變評價導向，使學生不僅關注計算技能，更關注算理的理解，以適應新的教學需要。要改變以往重“技能”而輕“算理”的教學弊端，引導學生“法理”并重，積極開拓數學思維，努力學好數學計算。

參考文獻

[1]潘可可，唐彩斌.發展學生運算能力應當“法理并重”[J].小學教學：數學版，2016（5）：13-15.

[2]蔣敏杰.小學數學計算教學算理的結構分析及教學策略[J].中小學教師培訓，2016（7）：37-42.