如何上好復習課

王雪平 李強

新授課結束后，部分學生對新知識處于似懂非懂的階段。此時，開展整理和復習教學，能夠起到理清思路、明曉算理、鞏固內化的作用。如何設計一節復習課？筆者結合三年級下冊《兩位數乘兩位數》的整理和復習教學，談一談自己的看法。

一、自主回顧梳理，培養分析觀念

回顧梳理環節，筆者主要借助“學習單”，引導學生自主復習。“學習單”內容如下：

1.通讀教材中的例題，想一想每道例題主要學習的是什么？

2.哪些題在什么地方容易出錯，請你用彩筆標一標，提醒自己。

學生通過梳理發現，本單元的口算例題有三種類型，像5×10、9×10這類“一位數乘10”的口算題，直接在一位數后面添上一個“0”就得出了積;像40×20、30×200、310×30這類“兩位數乘整十數、整百數”的口算題，用因數“0”前面的數和另一個因數“0”前面的數相乘，最后看兩個因數末尾一共有幾個“0”，就在積的末尾添上幾個“0”;像15×6、230×4這類“兩位數、幾百幾十數乘一位數”的口算題，將兩位數拆分成整十數和一位數，分別乘以另一個乘數，再把所得的積相加。

有關筆算的教學，教師通過再現“14×12=”的點子圖，讓學生體驗計算的實質，理解算理和計算方法。復習時，教師為學生提供直觀的點子圖作為研究素材，讓學生的思維軌跡在點子圖上留下足跡。教師先讓學生拿出點子圖（如下圖），畫一畫，再和同桌說一說筆算14×12的計算方法。

1 4

× 1 2

學生做完后，教師請學生展示，并說一說兩位數乘兩位數的計算方法。大部分學生是這樣計算的：先用乘數“12”個位上的數去乘以另一個乘數，得數的末位與乘數的個位對齊;再用這個乘數十位上的數去乘以另一個乘數，得數的末位與乘數的十位對齊;最后把兩個積相加。也有學生用“14”乘以“12”各個數位上的數。方法雖然有差異，但都是采用“先分后合”的思路，這一點恰恰就是乘法豎式計算的基本思路。這樣教學把直觀與抽象結合起來，使學生在明理中順利、自然地掌握了算法，促進了學生思維的發展，提高了學生的運算能力。

二、形成思維導圖，提升模型思想

復習階段，對于知識的梳理，最終應該形成知識網絡圖，讓學生能直觀地發現知識點之間的聯系，體驗知識的完整性和條理性，使學生對知識的理解和掌握更準確、更全面。

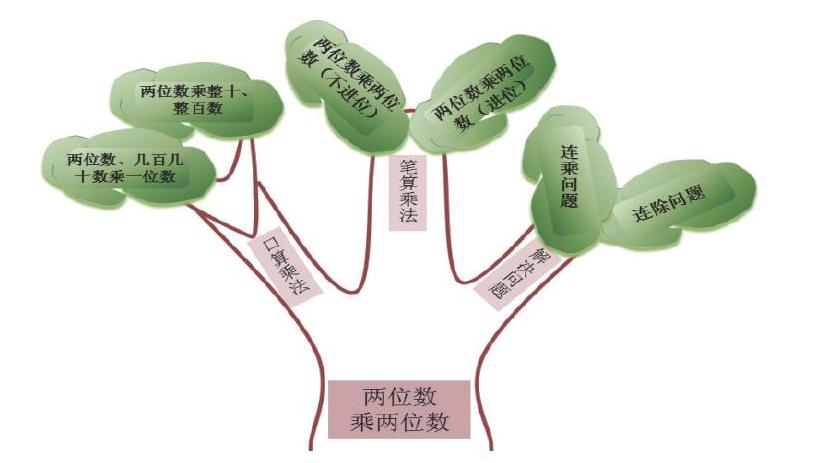
《兩位數乘兩位數》復習教學中，學生梳理了相關環節、在充分讀書的基礎上，教師收集學生的學習成果進行集中展示，形成“樹狀圖”。

師（出示一棵大樹的圖片）：看到這張圖片，開心嗎？

生（齊）：開心。

師：可別小瞧了這棵樹，它可不是一棵普通的樹，如果我們把剛才整理的這些知識移到這棵樹上來，它就變成了一棵知識樹。想想看，我們可以用樹干表示什么？

生1：兩位數乘兩位數。

師（指三根主枝）：這三根主枝表示什么？

生2：口算乘法、筆算乘法、解決問題。

師：口算乘法上面的分枝又表示什么呢？

生3：兩位數、幾百幾十數乘一位數（進位）;兩位數乘整十、整百數（不進位）。

師：筆算乘法包括哪些內容？

生4：兩位數乘兩位數（不進位）;兩位數乘兩位數（進位）。

師：解決問題包括哪些內容？

生5：連乘問題，連除問題。

教師根據學生的回答，將關鍵詞寫到大樹的相應部位上，一棵完整的知識樹就形成了（如上圖）。這棵樹其實就是一幅思維導圖，長期進行這樣的訓練，學生的模型思想就會逐步形成。

三、鞏固拓展實踐，強化應用意識

復習課應著重復習重點和難點問題。兩位數乘兩位數的重難點是末尾不是0的兩位數乘兩位數的計算方法。針對重難點，筆者引導學生自主設計練習題。學生設計了以下三類題：

1.口算：24×3、24×30、240×300。

2.筆算：54×39、123×23。

3.填空： 2

× 3

（想一想：積可能是幾位數？在兩個因數的末尾，填出一個數字，算一算。）

學生自主完成練習后，教師引導學生分享學習成果。

師：口算題“240×300”已經是三位數乘三位數了，我們應該怎樣口算？

生1：雖然位數超出了我們的學習范圍，但實際上是兩位數乘一位數，與我們本單元學習的內容是一致的，先算出24×3的積，再在后面添上三個0就行了。

師：123×23怎樣計算？出題的同學是怎么思考的？請出題的同學來當一回小老師，跟大家講一講。

生2：我發現用三位數乘以兩位數只是計算的位數增多了，積的位數隨著增多，其計算方法與兩位數乘兩位數是一樣的。

師：對第3道填空題，你是怎么判斷的？

生3：積可能是三位數，因為二十幾乘以三十幾，最多是六百多，應該是三位數。

師：其他同學有什么不同想法？在個位補一個數算一算。又有什么發現？

生4：也可能出現積是四位數的現象，比如29×39=1131，積是四位數。我們在計算時，要考慮到多種情況。

學生自主出題是這節課最大的亮點，它不僅讓學生有效鞏固了本節課的知識點，還引導學生進行了深層次探究，初步接觸到了四年級上冊才學習的三位數乘兩位數的筆算。

（作者單位：棗陽市鹿頭鎮吉河小學）