學情視角下小學數學課堂導入環節的設計

江蘇省吳江經濟技術開發區山湖花園小學 金怡婷

實踐表明，有效的課堂導入應立足于對學情全面而充分的把握，選擇合適的切入點和學生真正的興奮點，促成其主動地、積極地參與學習，為學生的進一步探索搭橋鋪路、提供支持。

一、復習式導入：把握認知基礎，點醒知識儲備

比如，在教學乘法和加減法兩步混合運算時，老師出示這樣的混合運算：32+3-20,56÷7×8，并依次提問：“先算什么，再算什么？”學生回答：“先算加法，后算減法。先算除法，后算乘法。”教師追問：“運算順序是怎樣的？”學生回答：“從左往右的順序運算。”同級與不同級混合運算之間有聯系，有不同，同級運算是不同級運算的知識基礎，但也極易產生不同級混合運算學習的負遷移。因此，在導入環節中用復習舊知的方式，明確同級混合運算的運算順序，將新知與舊知自然地建立起聯系，排除兩者之間的相互干擾。

又如，在教學平行四邊形的面積時，老師出示這樣的練習：圖中每個小方格的邊長都是1厘米，涂色圖形的面積各是多少平方厘米？（下圖依次出現）

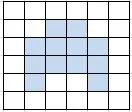
在計算平行四邊形的面積時，用到的方法就是將平行四邊形“轉化”成長方形來計算其面積。而“轉化”這種方法在學生解決以往問題時，便已有意或無意地習得并運用。教師從這一舊練習入手，從最簡單的長方形開始，到移動某些小方格形成的不規則圖形，再到其中有部分不是滿格的圖形。一步步，循序漸進，慢慢在頭腦中使“轉化”的思想開始明晰，原來新的、復雜的圖形都可以轉化成舊的、簡單的圖形，于是便“新的不新，難的不難”。

架通新知與舊知的過程既是一個理性思辨的過程，又是一個促成有效學習發生的過程。

二、生活式導入：尊重認知取向，點燃學習熱情

數學從來不是冰冷的公式，也不是拒人于千里之外的證明，數學教學可以是親和的、浪漫的、熱烈的。著名的數學家弗賴登塔爾認為，數學生發于普通常識，數學教育必須聯系生活實際。對小學生而言，數學知識在一定程度上其實是舊知識，因為在其生活中已經有了許多關于數學的體驗。可以認為，數學課堂的學習是生活知識的系統化與規范化，是生活經驗的深化與升華。因此，課堂導入可以是生活化的，讓學生從現實世界出發，走向教材中的數學王國，讓學生愛上數學、樂學數學，點燃創造學習的熱情。

例如，在教學平移和旋轉時，老師為學生展示了豐富的素材，不同于書本上靜態的圖片，而是播放了大量的視頻，具象學生對平移與旋轉運動的特征，豐富學生的空間感知。同時，老師在選材時尤其注重資源的新鮮度與熱度，牢牢抓住學生的興奮點，讓學生在學習數學知識的同時，拓寬視野、提升綜合素養。例如，“2017年國慶前后，京滬高鐵將全線提速，高鐵是怎樣運動的？”“游泳錦標賽上跳水的頒獎儀式，看國旗是怎么運動的？”這些例子鮮活而貼切。更值得一提的是，老師讓每一個學生自己動手去體驗，去感悟運動的本質特征，并且為了感知得更加生動與準確，教師讓學生借助一些實物工具進行操作，例如“用鉛筆演示高鐵的運動”“用橡皮演示國旗升起的運動”。學生將看到的現象通過自己的動作來進行示范，在這種活動中更加深化了對運動本質的認識。

三、問題式導入：提供認知條件，點亮思維火花

學習數學，學生需要一定的認知條件，除了我們所熟知的資源與輔助工具外，更需要特定的觸發劑，問題是思維的觸發劑。

比如，在教學長方形和正方形的面積時，某老師在黑板上寫下了一個字——“面”，并提問：“你對‘面’有怎樣的理解？”從學生最初對“面”的理解為切入點，讓學生展開豐富的聯想，“黑板面”“課桌面”……再回到學生所熟知的“課本封面”進行手掌的觸摸，讓學生在摸的過程中逐步感受到生活中的物體都有面，并且面有大小，從而引出“面積”的概念。接著，“你想知道哪些和面積有關的問題？”啟開了對“面積”的探究。格式塔心理學表明，知覺是具有整體性的，人在對知覺客觀事物各要素之間的內在聯系后，會產生理解和頓悟。這位老師通過提出問題，給學生建立起一個有關事物的整體形象的認識，碰撞出學生思維的火花。

此外，當學生原有的知識經驗和認知結構與將要學習的知識內容出現認知矛盾和沖突時，往往容易產生心理困惑，這就引起了學生認知心理的不平衡，進而激發起學生自主探究、解決問題的動機。

四、實踐式導入：積累認知經驗，點沸數學素養

認知經驗不同于認知基礎，是在學習過程中形成的比較穩定的思維方式，比如判斷、歸納、推理等思維品質。它不能直接解決問題，但卻為解決問題提供了思路和方向。因此，在數學教學中，我們應格外注重培養這些品質，促成學生素養的發展。實踐式的導入，有助于學生認知經驗的積累。

眾所周知，圖形的認識是一個抽象的過程，我們的教學要聚焦核心內容和教學重難點，讓學生經歷抽象出圖形的過程。很多老師在教學認識線段時，都有這樣的導入設計：他們給每位學生都提供了一根毛線，然后讓學生想辦法把毛線變直。二年級的學生經過活動，發現可以捏住毛線的兩端用力一拉，這樣毛線就變直了。通過這樣的直觀操作，把線段這一抽象的圖形具象了，兩手間的一段可以看成線段，兩手捏著的兩個點便是線段的兩個端點。同時，學生已然可以知道線段的特征，即直的、有兩個端點。

又如有位老師在教學認識圓柱和圓錐時是這樣設計導入環節的：老師給學生提供豐富的圓柱和圓錐實物模型（底面半徑相同、高相同的圓柱和圓錐；底面半徑不同、高相同的圓柱和圓錐；底面半徑相同、高不同的圓柱和圓錐等），大膽放手，讓學生自主探究發現圓柱和圓錐的特征，采用開放式的實踐活動，讓學生在自主探索、同伴交流、小組合作的過程中，通過觀察、比較、猜想、歸納等思維活動，一步步實現圖形抽象的過程，實現學生素養發展的過程。

課堂導入是一節好課的關鍵第一步。正所謂“教學有法，教無定法，貴在得法”。導入的具體形式是多種多樣的，但其最根本的是要準確把握學情，從學生的認知基礎、認知取向、認知條件、認知經驗等方面入手去設計導入環節，真正實現“以學定教”，從而使數學課堂更精彩，數學學習更有效。