暴露思維慣性 提升思維廣度 增強解題能力
——以高三三角函數拆角技巧求值復習課為例分析

浙江 陳啟超

筆者通過課堂上復習三角函數求值時發現學生對于學過的拆角技巧求值基本不會，大部分學生采用解方程的思想解題.為什么教過的方法學生不會用，而解方程的方法卻有那么多的學生采用.從中反思：學生受習慣思維的束縛，按部就班，缺少獨立求異的思維，這對學生的發展是不利的.筆者通過對學生學情和教師教學的分析，提了幾點突破思維習慣的建議：一是暴露學生原有的思維框架，改善學生的思維習慣；二是加強變式教學，拓展學生思維廣度；三是防止解題教學的簡單化，提高學生思維深度，與大家共勉.

1．問題提出

在高三的一節三角函數復習課上，筆者給出這樣一道題目：

據課堂上觀察，學生的做法主要有以下兩種：

一種是(很多學生采用的方法)解方程的思想方法：就是利用兩角和的正弦公式將sin(α+β)展開，得到sinβ，cosβ的一個關系式，再結合sin2β+cos2β=1去解cosβ.在給定的時間內，很多學生還沒算出答案，有的甚至中途放棄了.

另一種是利用拆角的技巧：把β看成是(α+β)-α，則cosβ=cos[(α+β)-α]利用兩角差的余弦公式展開計算.但這種方法用的學生很少，一個班就五六位學生左右.

筆者在另外一個班也給出這道題進行試驗，結果大致一樣，學生大部分選擇了解方程的思想.課后，筆者想：拆角的方法思路巧妙，過程簡潔，課堂上也講過這種方法，但為什么過了一段時間后能順利求解這一問題的學生那么少.這說明平常將看似很好的方法直接灌輸給學生，其教學效果是很低的，學生對解題方法的認識只停留在賞析的層面上，沒能在大腦中留下深刻的印象，對拆角的方法并沒有深刻的理解.我們可以想象，如果下次再出現類似的題目，還是有很多學生用解方程的方法.好的方法學生不會用，為什么會如此？ 這是值得思考的一個問題.

2．原因分析

2.1 學生的想法

課后筆者找了幾位學生談心,經過訪談了解到學生的一些想法.

甲同學認為(基礎較好)：平時在求解三角函數值時經常是利用同角三角函數關系式求解，大部分就是解方程的方法.一看此題，就發現和原來做的很類似，而且利用sin(α+β)展開，容易找到sinβ，cosβ的關系，再結合sin2β+cos2β=1，很自然就想到消元解方程了，就是沒想到計算會那么復雜.

學生乙：(頭腦靈活，平時有點懶)：讀完題目，很快就找到了題目的突破口，聯立方程求解，計算沒什么意思，就不算了，主要是方法知道了就可以了.像乙這類學生平時缺少思考，學習習慣不怎么好，只會耍點小聰明.

學生丙：曾經碰到過類似題目，嘗試過解方程，解起來很困難，后來聽老師講解拆角的方法，印象很深.對三角函數的求值問題，不同的類型要選擇不同的方法.對于此題試過解方程，但發現計算量大，就嘗試用拆角來解，沒想到就很方便的解出來了.

2.2 教師的看法

聽了學生的想法，筆者也對任課的部分老師做了探討性的調查.經討論，對學生的這種解法主要歸結為兩個方面：一是這類題目本身具有一定的難度，拆角是一種技巧，對學生的數學思維能力要求比較高.在學生的思想中，α+β始終是看成兩個角的和，α，β才認為是一個單獨的角，也就是對整體思想的理解還不夠，所以學生很難想到把β看成是(α+β)-α.二是學生受到慣性思維的影響，一看到這道題目就自然而然想到解方程，這個想法是很自然的.但對于一個二元一次方程和一個二元二次方程構成的方程組，通過消元之后，雖然只有一個變量，但往往難于因式分解，要用求根公式來解，結果很多學生就被計算給卡住了.

2.3 心理學視角

這次解方程解不出來，下次碰到了大部分學生還是解方程.而且現在這一屆學生如此，換了一屆學生仍會出現同樣的問題，這可能也有心理學上的原因吧！

在心理學上，學生的這種現象叫做思維慣性.什么是思維慣性呢？從心理學上講：我們把這種按照積累的思維活動、經驗教訓和已有的思維規律，在反復使用中所形成的比較穩定的、定型化了的思維路線、方式，叫做思維慣性.簡單地說：就是以前怎么做，我現在就模仿著做.

思維慣性一方面有利于學生按照一定的程序思考數學問題，比較順利地求得一般同類數學問題的答案.另一方面這種習慣思維又會帶來負面效應.學生由于受思維習慣的影響，不注重變換思維的方式，缺乏探索解決問題的途徑和方法，缺少了思考的空間，這對學生思維能力的培養是不利的，從而也影響到學生解題能力.

那么，作為一線教師，我們該怎么做呢？筆者通過自己的教學實踐，提出了幾點改善的措施.

3 .改善措施

3.1 暴露學生原有的思維框架，改善學生的思維習慣

就如本文開頭講的這道三角函數的求值問題.雖然教師在課堂上講過拆角的方法，但是過了一段時間讓學生做，還是有一大部分學生利用解方程的方法.既然這樣，教師就讓學生順著他們的思路往下解，而不是馬上否認此方法不行.讓學生出錯，摔跟頭，讓他們從錯誤中尋找原因，要讓他們經歷困難和挫折，才能感受深刻.

本題學生錯的主要有以下一些步驟：

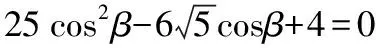
②聯立得到的一元二次方程還要用求根公式求根，學生求根公式經常算錯.(能解出一元二次方程的根的學生寥寥無幾)

③即使解出來了根還得檢驗，可能會有增根.(做到這步的學生幾乎沒有)

既然解方程過程這么麻煩，那有沒有其他的方法呢？這時再講解拆角的方法，學生就有一種豁然開朗的感覺.通過兩種方法的對比，讓學生切身體驗到第二種方法的簡便和優點.成功的體驗不僅限于結果，還有思考的過程，有時過程比結果更精彩.回想教師自己，可能第一次解這類題時也是用解方程的方法，通過不斷地積累、思考以及認知的提高，自身的思維能力和解題能力也在逐步提升.學生正處于積累經驗的初期，在解題中培養學生悟性尤為重要.我們可以以典型題為載體，讓學生經歷失敗與成功，培養學生多嘗試的思考模式和探究習慣，這是一條突破學生慣性思維的有效途徑.

3.2 加強變式教學，拓展學生思維廣度.

如:函數f(x)=x2+bln(x-1),其中b∈R，若f(x)在其定義域內單調遞增，求b的取值范圍.雖然是高三的學生了，但還是有很多學生是這樣解的：

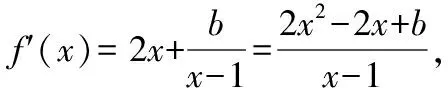
從學生的解答過程中，可以看出，學生的思維還停留在初中的水平上，對于二次函數的恒成立問題，學生習慣性的認為定義域是R，第一反應就是Δ≤0，他們的這種習慣思維導致此題失誤.那么在課堂上，筆者不如這樣來設計：已知函數f(x)=2x2-2x+b，

①對?x∈R,恒有f(x)≥0,求b的取值范圍.這個學生很擅長，基本沒問題.

②對?x∈[1，+∞),恒有f(x)≥0,求b的取值范圍.這是二次函數定區間，定對稱軸問題，但注意此時對稱軸并不在定義域內，則要結合定義域求最小值.

③若f(x)=2x2+bx+2,當x∈[-1,1]，f(x)≥0,求b的取值范圍.二次函數定區間，不定對稱軸，此時要討論對稱軸的位置.

上述設計層層遞進，每做完一題，適時指出解決這類問題的要點以及前后兩題之間的聯系，讓學生關注定義域在解決函數問題中的作用.因為很多學生對于二次函數問題，習慣的認為其定義域是R，所以要改變他們的這種習慣的思維.通過變式，加深了學生對函數概念的理解.定義域變了，即使對應法則不變，函數也是跟著變的.所以在解函數問題時首先要關注函數的定義域.通過這樣的練習，他們對函數的概念有了進一步的理解，學生的思維空間得以提升，想問題，做事情也就會考慮周全，這是一種好的思維習慣.好的思維習慣的養成，對消除學生的思維慣性和培養學生的思維邏輯能力有很大的幫助.

3.3 防止解題教學的簡單化

高三復習常常是以解題教學為主，因為復習的內容多，時間緊，很多老師往往分析了題目的思路，然后進行歸納，形成套路，沒有分析題目所蘊含的數學思想和方法，就題論題的教學對學生的思維能力的提高是不利的.

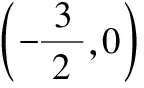
①方法上的拓展，平面幾何和解析幾何不是單獨的兩個內容，他們之間有著密不可分的聯系.本題還可以利用橢圓第二定義及三角形相似這樣來解：

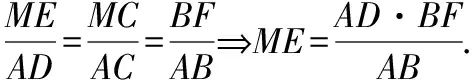
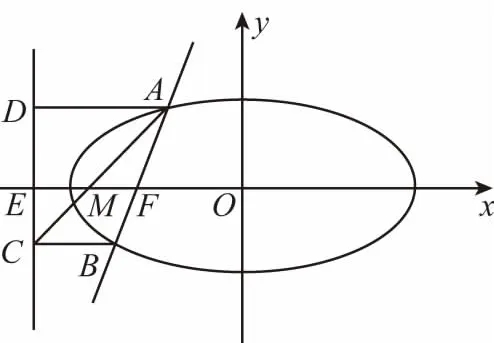
把①式代入②③中即可得ME=MF，學生驚嘆，好簡單呀！教師也可順著思路講到在歷年的高考題中也經常會出現用平面幾何知識來解圓錐曲線的題目.如：

( )

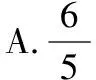
利用第二定義解比較方便.

②結論的延伸，本題的曲線是橢圓，那么換成雙曲線或是拋物線是不是還有類似的結論呢？感興趣的學生興致就被提上來了.課后學生通過獨立思考和探索，有學生說其實就是一個定值問題，等價于直線AC經過一個定點.那么，還可以進一步思考，若F點改成其他的橢圓內的與x軸的交點，定直線是準線外的其他直線，直線AC是否還經過定點呢？通過這樣的變式教學，學生的思維也漸漸展開了，對題目的研究也就深了，思維的空間得到了拓展，增強了學生解題的悟性.若是碰到新題、活題，學生思考問題的空間也就不再是那么的固定和狹隘，對學生解題能力的提高是很有利的.

4.結束語