例談數學課堂導入的方法

江蘇 雷亞慶

我們知道好的開始是成功的一半，好的課堂導入也是課堂教學取得良好效果的基礎與關鍵.精心設計的課堂導入設疑激趣，能夠迅速調動學生思考的積極性，引導學生進入特定的情景之中，從而進入最佳學習狀態，獲得良好的課堂效果.

一、復習導入

通過對原有知識的復習提問，引導學生發現問題，提出問題.復習導入要熟悉學生原有的認知水平，精心選擇復習與提問的支點，“溫故知新，由舊導新”.

案例1：《直線的方程》的導入

問題1：直線斜率的意義是什么？斜率公式是什么？

問題2：已知直線過點(-1，3)，斜率為-2.試寫出該直線上另一點的坐標.

問題3：這樣的點有多少個？

問題4.這些點的坐標滿足什么關系式？

問題5：問題一般化，如果一條直線過定點，斜率為k，這條直線上的點的坐標滿足什么關系式呢？

通過復習前節課所學內容，引導學生自主探究直線方程，甚至建構直線方程的概念.

二、作業糾錯導入

學生通過糾正作業中錯誤的過程，深化對數學概念的理解，同時對正確的解法充滿期待，從而順利導入新課的學習.

案例2：《求非等差非等比數列的通項公式》的導入

師：對于昨天的作業：已知數列{an}中，a1=1，an+1=an+n，求數列{an}的通項公式.很多同學是這樣做的：

∵an+1=an+n,

∴an+1-an=n,

∴數列{an}是等差數列.

∴an=a1+(n-1)·d=1+(n-1)n,

即an=n2-n+1.

這種解法正確嗎？

生1：我認為不對，因為等差數列的通項公式應該是關于n的一次函數形式，而這種解法所得的結果卻是二次函數.

師：那么此解法錯在哪里呢？

生2：已知條件不符合等差數列的定義.它的每一項與前一項的差不是同一個常數.

學生紛紛點頭表示同意.

師：看來錯誤的原因是我們對等差數列的概念理解不準確.那么這個數列的通項公式到底如何求解呢？

糾錯導入達到了兩個目的：一是加深了對等差數列的定義的正確理解；二是在尋求正確解法的過程中自然地導入了求其他數列通項的學習.

三、游戲導入

通過設計與新課內容相關的小游戲，增加趣味性，可以迅速吸引學生的注意力，使學生的思維順勢進入新課的正確軌道.

案例3：《不等式的證明》的導入

師：同學們來猜一個謎語， “考試不偷看”，猜一數學名詞.

生：真分數.

師：很好，現在請大家任意寫下一個真分數，然后在分數的分子和分母分別加上同一個正數，新的分數與原分數的大小關系如何？

生： 變大了.

師：大家能否得到一個一般性結論呢？

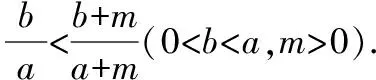
師：能否證明？

學生都希望證明自己發現的結論，所以很快地進入了思維的狀態.

四、實驗導入

實驗導入是根據學生學習之初的心理活動特征，設計演示實驗，讓學生在實驗中感悟數學，建構數學，激發學生的學習興趣.

案例4：《立體幾何引言課》導入

師：用五根吸管可以搭成幾個正三角形？請大家動手搭搭看(教師事先為同學們準備好了塑料吸管，四人一組，合作交流).

生很快搭出兩個正三角形.

師：六根吸管能否搭出四個正三角形呢？

學生在平面內始終無法完成.經過小組討論和實驗，終于擺出了正四面體.

師：大家在實驗的過程中體會到有些問題在平面內無法解決，需要把目光放到空間里去考慮.這就是我們接下來要學習的空間幾何.

學生在實驗的成就感中開心地進入立體幾何章節的學習.

五、數學史導入

在數學發展歷史中有很多動人的故事，通過故事導入，可以使學生對所學內容產生濃厚的興趣，激起強烈的求知欲望.

案例5：《等差數列前n項和公式》的導入

師：大家知道德國著名的數學家高斯嗎？他被人們稱為數學王子.

生點頭.

師：高斯在學生時代就顯示出與眾不同的數學能力.有一次老師出了一道題目，其他同學剛剛動筆，他便算出了答案.大家想不想知道他當時做的題目是什么，他是如何做的？

生點頭.

師：這個問題就是計算“1+2+3+4+…+100”，當時高斯很快就得出答案，下面同學們也來挑戰一下高斯如何？

學生情緒高漲，迅速拿筆嘗試起來，很快進入教師期望的課堂狀態之中.

六、生活情境導入

生活中處處有數學，由生活中的實例導入新課，既可以激發學生的學習興趣，又符合學生從實踐到理論，從感性認識到理性認識的認知規律.

案例6：《函數的周期性》的導入

師：同學們，我們一學期有一百多天的課，可為什么我們教室里只有五天的課表呢？

生：周一至周五的課表，加上周六和周日，每隔七天會重復出現，所以只要五天的課表！

師：說得非常好，實際上這位同學說的是一種我們生活中常見的周期現象，大家還能舉些類似的例子嗎？

生：還有四季輪回，地球公轉，潮漲潮落，還有勻速圓周運動等等.

師：是的.那么這些周期現象如何用數學的方法表示呢？這就是我們今天要學習的函數的周期性.

由學生十分熟悉的課表出發引出生活中的周期現象，既符合學生原有的認知基礎，又很自然地過渡到函數周期性的學習.

七、設疑導入

設疑導入是利用一些暫時懸而未決的問題，與學生已有觀念形成認知沖突來導入新課的方法.

案例7：《數學的擴充》的導入

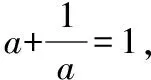
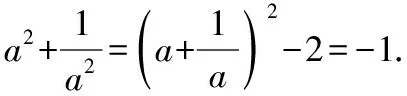
師：大家想知道個中緣由嗎？奧秘就在我們即將學習的新課中.

學生興趣盎然，積極投入到復數的學習中去.

設疑導入方法使學生置身于矛盾之中，激起他們解決矛盾的強烈愿望，促使他們積極主動地學習新的知識.

八、相關學科導入

數學是自然科學的基礎學科，和其他學科特別是物理學科有著密切的聯系.導入新課時，如果從這些學科的問題出發，既符合學生的認知，又容易引起學生的興趣，從而順利導入新課.

案例8：《任意角》概念的導入

師：函數是反映客觀世界變化規律的最基本的數學模型，比如說，在我們初中學過的勻速直線運動中，當速度是100時，路程s與時間t的關系可以用什么函數來刻畫呢？

生 ：s=100t，所以是正比例函數模型.

師：那我們高一物理剛剛學過的勻加速直線運動中，當初速度和加速度固定時，末速度v與時間t以及路程s與時間t的關系可以用什么函數模型來刻畫呢？

生 ：一次函數模型和二次函數模型.

師： 很好！從剛才的例子中我們可以看出現實生活有很多有規律的現象是可以通過函數模型加以刻畫和研究的.下面我們再看看這樣一種運動可以用什么函數模型來刻畫呢？

學生充滿好奇與期待.

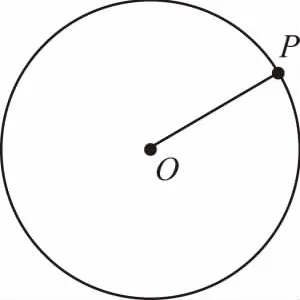
師：如圖，點P在半徑為r的圓O上繞著圓心O做勻速圓周運動(教師用幾何畫板演示圓周運動，學生認真觀察)，請同學思考以下問題：

點P的運動有何規律？

生：點P在圓上不停地轉動，而且OP在繞點O轉動時形成一個角.

生：而且每轉一圈會回到原來的位置.

師：很好！大家發現點P的運動呈周而復始，循環往復的特點，實際生活中有這種規律的現象還有哪些？請大家試著舉幾個例子.

生：摩天輪，水車.

生：地球公轉，鐘表，月圓月缺，潮漲潮落，四季更迭，每7天一個星期.

師：實際上還有很多這樣的現象，這現象都呈周而復始、循環往復的特點，我們可以稱之為周期現象.大家想想我們學過的函數有沒有可以刻畫這種周期現象的函數呢？

生：我覺得如果一個函數可以描述周期現象的話，它的圖象一定是具有來來回回周而復始的特征的，但是我們學過的函數中沒有哪個函數的圖象是具有這樣的特點，所以我們學過的函數中沒有哪個函數是可以刻畫周期現象的.

師：說得非常好.因為我們學過的函數中沒有可以刻畫周期現象的.因此我們需要學習新的函數來刻畫周期現象.這就是我們本章要學習的三角函數.那么要研究三角函數，顯然要從“角”談起.(老師板書課題“角”)