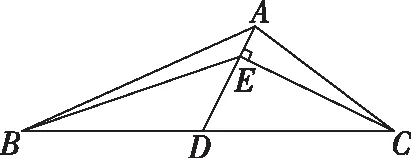
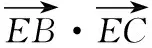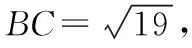高考復習課貴在題精法多真參與

江蘇 宋衛東

解題教學是高考數學復習課的重點和核心．美國著名數學教育家G·波利亞說過：“一個專心的認真備課的老師能夠拿出一個有意義但又不復雜的題目，去幫助學生挖掘問題的各個方面，使得通過這道題，就好像通過一道門戶，把學生引入一個完整的理論領域．”一節課教師通過一個問題(例題)的引領，讓學生積極參與教學，并根據自己的認知，從不同的角度思考問題，做到一題多解，借題發揮，從而產生思維的碰撞，進而理解數學的本質，掌握解決數學問題的規律和方法，達到“做一題，通一類，會一片”的目的，從而提升學生的數學核心素養．近日筆者在高三教學視導中聽了一節復習課，上課教師一節課就處理一道習題，學生們主動參與課堂，積極思考，從不同的角度探尋出不同的解法，教師及時參與其中并適時點撥、總結，教與學的氛圍濃厚，給筆者留下深刻的印象．

一、課堂簡錄

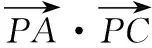
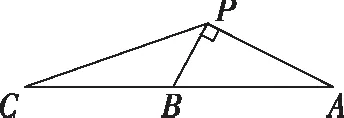
教師出示習題，學生獨立思考、嘗試10分鐘，然后組內討論5分鐘左右．

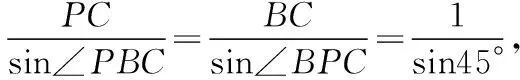
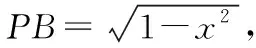
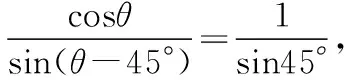
教師：同學3，你是怎么想到設∠PBA為θ的呢？

學生3：設∠PBA=θ后，可以用θ的三角函數來表示其他的量，相比剛才的兩種解法就減少了未知數的個數．

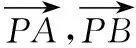
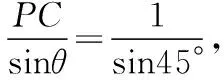
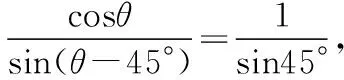
∴sin45°cosθ=sin(θ-45°)，∴sinθ=2cosθ．又sin2θ+cos2θ=1，

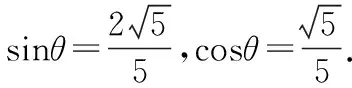
MRI，即磁共振成像，在臨床上有著良好的應用，尤其是在對顱腦、脊髓、心臟大血管等進行成像檢查，其效果最佳。因此，采用MRI對兒童進行垂體結構和病變的觀察，其效果良好，而且該檢查方式是檢查異位垂體后葉的唯一影像學方式。而3.0T MRI，其組織對比度、化學位移分辨率、磁敏感性對比都明顯較高，不僅可以對顯示細微解剖結構進行優化，還可以有效提高影像的分辨率。不僅如此，在相同信噪比的基礎上，3.0T MRI還可以提高采集的速度[4]。

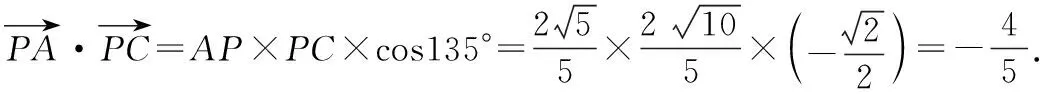
教師：以上三位同學都是從設∠PBA=θ入手，剛才說了同學3利用基底法，同學4是用了間接法兩邊平方求數量積，同學5與同學1相同，是運用定義法求數量積，只是處理的方式不同．還有其他解法嗎？

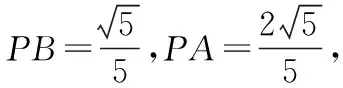
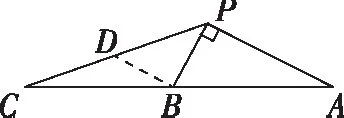
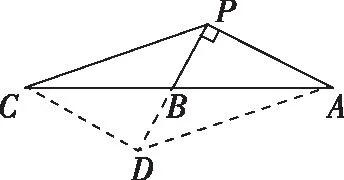
教師：同學6，你是怎么想到過點B作PB的垂線的呢？

學生6：我的想法是把45°放到直角三角形中，進而利用中位線定理和勾股定理求AP，PC的長度．

教師：很好，同學6是運用幾何法求線段的長度，思路清晰，過程簡捷，還有沒有同學采用另外的幾何法來做的？

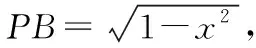
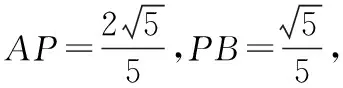
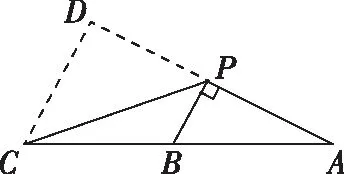
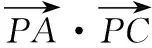
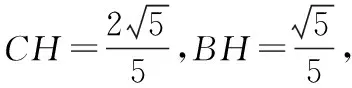
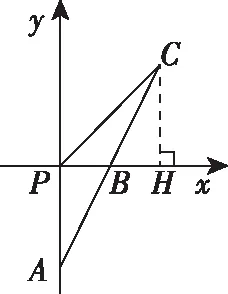
教師：漂亮!你是怎么想到要建系的呢？

學生9：我是將直角放到平面直角坐標系中，發現能求出各個點的坐標，因此采用坐標法求平面向量的數量積的．

教師：還有沒有不同的建系方法呢？

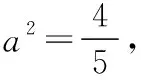
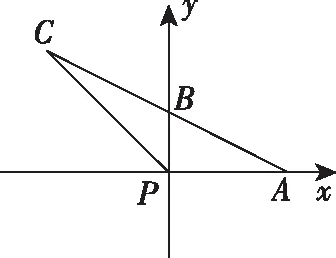
教師： 同學9與同學10都是從坐標入手，利用直角建立平面直角坐標系，通過確定各點的坐標求出平面向量的數量積．請同學們思考，什么時候能利用建系的方法求向量的數量積呢？

學生11：常見的三種情況：一是題目中有垂直(直角)；二是題目中有特殊角，比如30°，45°，60°，120°，135°等；三是利用對稱性建系，比如橢圓等圓錐曲線的標準方程的建立就是利用對稱性建系的．

教師：很好．還有其他想法嗎？(學生均表示沒有)

教師：定義法、基底法、坐標法、幾何法是處理平面向量數量積問題的法寶，請同學們課后針對這個題目進行整理、總結和體會．本節課就上到這里．

二、幾點思考

1.題不在“多”，有“思想”則靈

解題是學好數學的必要途徑．本節課教師由一個習題出發，放手讓學生獨立思考、探索發現，然后將話語權交給學生，通過生生互動、師生互動，讓學生自己探究解決．可以說這節課是深刻的、有思維深度的課．然而當前高考數學復習刷題成風，題海浪涌，學生苦，教師累．學習數學離不開解題，但沉溺題海并不意味著能考好數學，不如通過分析典型例題的解題過程來學會解題．題并不是刷得越多學生學習越好，如果缺乏解題反思，在沒有理解掌握的基礎上，學生做題越多，越會加深對錯誤做法的記憶，從而誤導他們的學習．因此，教師要精選有“思想”的習題作為課堂上的例題，高考數學復習課的成敗主要取決于例題的選擇，例題不在于“多”，更不在于“難”，關鍵在于學生能通過探究尋找出解題的切入點，教師通過適當的精講點撥，能與學生共同總結出解決問題的規律和方法，并探尋通性通法，提升學生解決問題的能力．教師在選取例題時一定要思考“為什么要選擇這道題目，此題與其他題相比優勢在哪里？通過解此題，對于解其他題有何幫助？”，從思維的鍛煉、能力的形成角度看，讓學生學會思考要比單純的解題訓練來得更深刻、有效．例題要少而精，要控制好難度，復習的目的不是為難學生，而是通過例題的解決來幫助學生鞏固知識，探尋解決問題的方法，激發學生的學習興趣，幫助學生更加有效地學習數學，促進他們數學核心素養的形成和發展．

2.“師獨演”不如“生紛紜”

啟迪學生的深度思維必須放手讓學生去發現，要把數學探究的主動權交給學生．本節課教師積極營造學生參與的氛圍，留出一定的時間讓學生獨立思考、嘗試，教師沒有將自己的解題經驗簡單地灌輸給學生，沒有用自己的想法代替學生的思維，而是讓學生的思維先行，允許學生提出自己的見解，讓學生去聯想、類比、探索并及時反思．學生每提出一種解法后，教師及時追問“你是怎么想到的”、“還有沒有其他的解法”，并與學生平等地交流和探討，及時地點評和總結，多角度揭示問題本質，拓寬解題思路，力求對解題規律進行深化，達到“做一題，會一類”的目的．教師要準確地把握學生已有的認知，要根據學生的不同需求而教學，才能尋求學生思維的最近發展區，提高教學的有效性．復習課中，確立學生的主體地位并不影響教師主導作用的發揮，教師要從理解學生出發，在教學生如何學習和思考上下功夫，解題后要引導學生思考：解此題用到了哪些知識？它們是怎樣聯系起來的？解題的關鍵在哪里？思路是怎樣打通的？還有其他的解法嗎？這種解法能用于其他問題嗎？哪種解法是通性通法？解法多時，教師還要注意解法的優化，一種解法更適合哪一類的問題情境，要給學生建模塑型．復習課教師一定要轉變教學觀念，轉換教學方式，要在精講點撥上下功夫，不要“一言堂”，要舍得花時間讓學生發表自己的意見，暴露學生的真實想法，在尊重學生認知的基礎上，讓學生會自主學習、探究學習、合作學習，從而引發學生的深度思維，讓課堂真正變成“學堂”．數學是自然的，不是強加于人的，只有沿著學生的思維方向探究、生成，這樣的復習才能和諧高效，才能真正彰顯“以人為本”的理念．

3.適當變式，讓例題煥發“生命力”

一題多解能夠訓練學生的發散思維，一題多變則能訓練學生思維的深度．本課由于時間關系，教師只做到解法上的訓練，而沒有進行問題的拓展變式，這不能不說是個遺憾．如果添加如下變式，教學效果則會更好．