一類帶負交叉擴散項的SIR傳染病模型的空間Turing斑圖
周 文,胡 偉,陳金瓊,凱 歌
(1.安徽師范大學數學與統計學院,安徽蕪湖 241002)
(2.北京工業大學機電學院,北京 100124)
1 引言
根據世界衛生組織的最新研究,傳染病依舊是人類死亡的第一殺手.由于對傳染病的研究不宜采用實驗的形式,因此理論分析與數值模擬常被用于傳染病的機理研究上.此時選擇合適的傳染病的動力學模型顯得十分重要,常見的傳染病模型有SI,SIR,SEIR等等.
在傳染病的動力學研究中,許多學者做出有意義的結果,特別是傳染病模型的空間斑圖動力學[1?4].孫桂全,靳禎等人研究了一類帶有時滯的SIR空間傳染病模型的Turing失穩,通過數值模擬得出了條狀與點狀共存的斑圖[1].王瑋明等人研究了一類SI傳染病模型,通過推導模型的振幅方程做出斑圖選擇,得到了不同類型的Turing斑圖[2].馬知恩和周義倉在研究中提出了這樣的一個比例依賴型的模型[5]
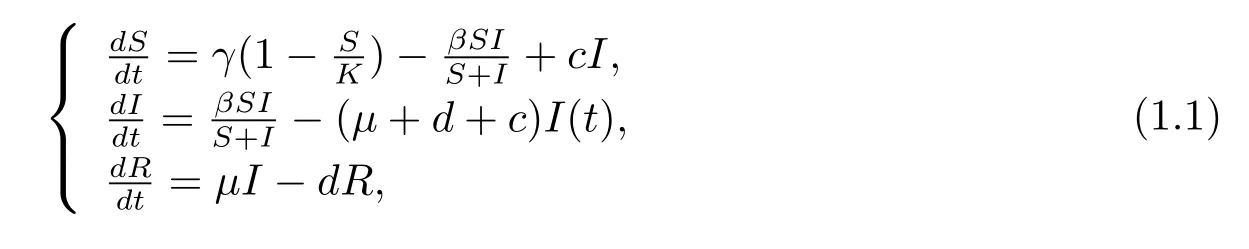
由于R與S,I無關,所以作者利用穩定性理論討論了下面一個微分方程組的平衡點的存在性與穩定性
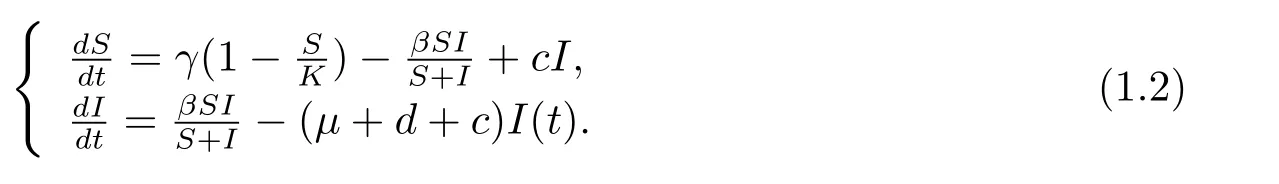
考慮到疾病對易感者與感染者心理上的影響,本文在此基礎上研究了一類帶有負交叉擴散項的SI傳染病模型
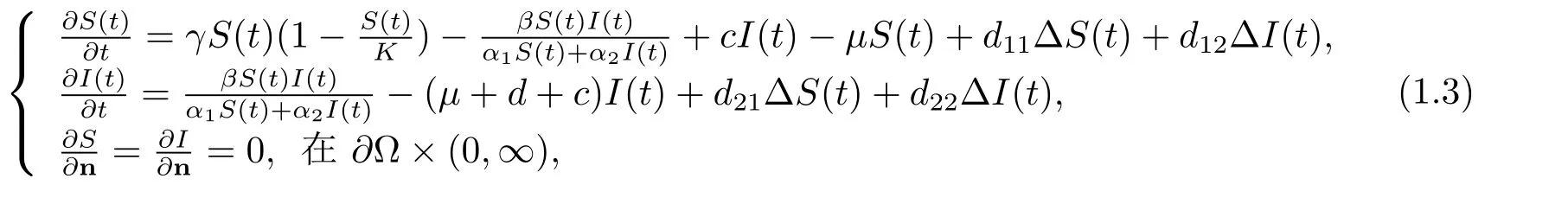
在這里S(t)和I(t)分別代表時間t時易感者和感染者的密度,γ和K分別代表了內稟增長率和環境的承載力,μ代表人口的自然死亡率,d代表了因病死亡率,c代表了染病者的恢復率,β是傳染病系數,是傳染率,α1和α2心理影響系數,并且α1和α2都是常數,?代表空間?中的Laplace算子,Neumann邊界條件表明模型(1.3)是自我封閉的,并且是零流量的,n代表著光滑邊界??上的單位外法向量.
這里需要指出的是,在之前的文獻[1–4]中,研究的傳染病模型所帶的交叉擴散系數都是正數,其生物學意義是人群總是從另一人群的高密度區域向低密度區域移動[6?7].而在實際生活中,人群從低密度區域向高密度區域移動的現象也是存在的.一方面,考慮到在生活中易感者有辨別染病者的能力并且會遠離染病者,同時染病者也會遠離易感者[6].另一方面,在疾病爆發初期,由于人們的心理因素,覺得人多的地方就是安全的地方,染病者反而會盡量接近易感者.所以在某種特定的情況下,這種染病者向易感者移動的現象在模型中則表現為交叉擴散系數為負數.據我們所知,帶有負交叉擴散系數的傳染病模型的Turing斑圖在生物模型中很少被研究.因此本文將研究帶有負交叉擴散系數的二維模型中的Turing斑圖的生成問題.
2 Turing空間的確定
首先考慮模型(1.3)
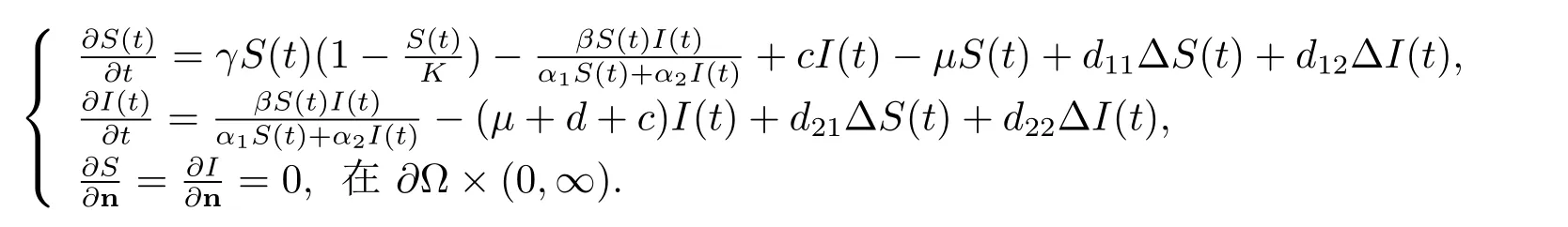
易知系統(1.3)有很多平衡點,包括E0=(0,0),穩定節點E1=(K(1?,0),和正平衡點E?=(S?,I?),從生物學上考慮,正平衡點更加有討論的意義,其中
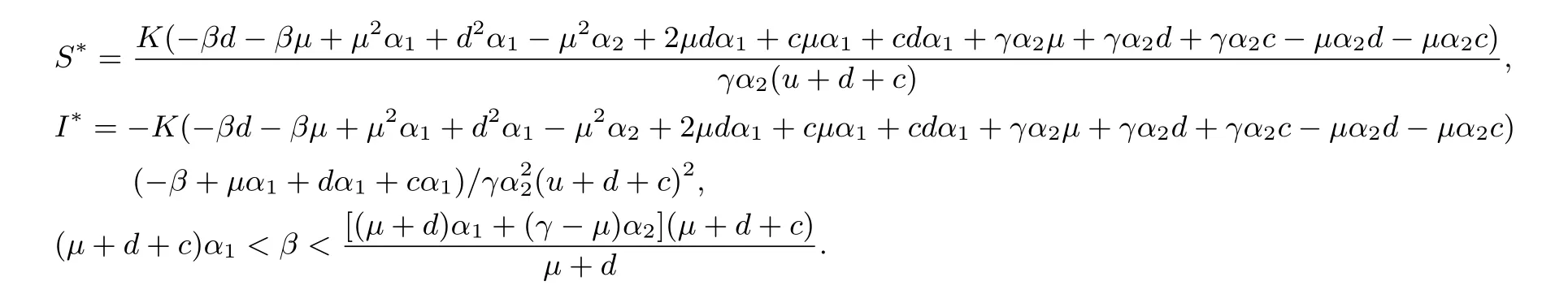
定理2.1不帶有擴散項的系統(1.3)的平衡點(S?,I?)是局部漸近穩定的.
證 為了討論方便,記
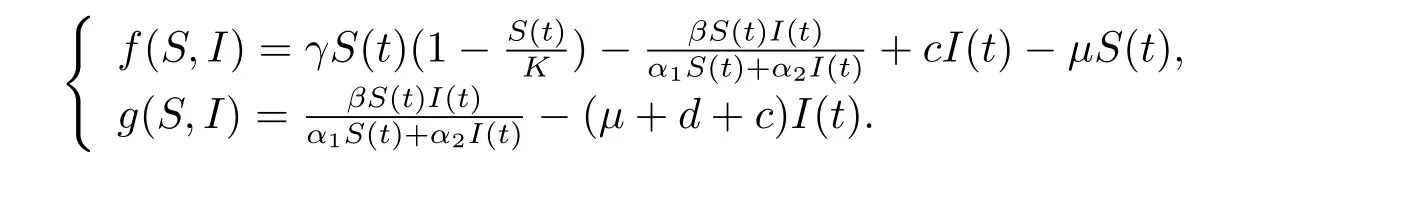
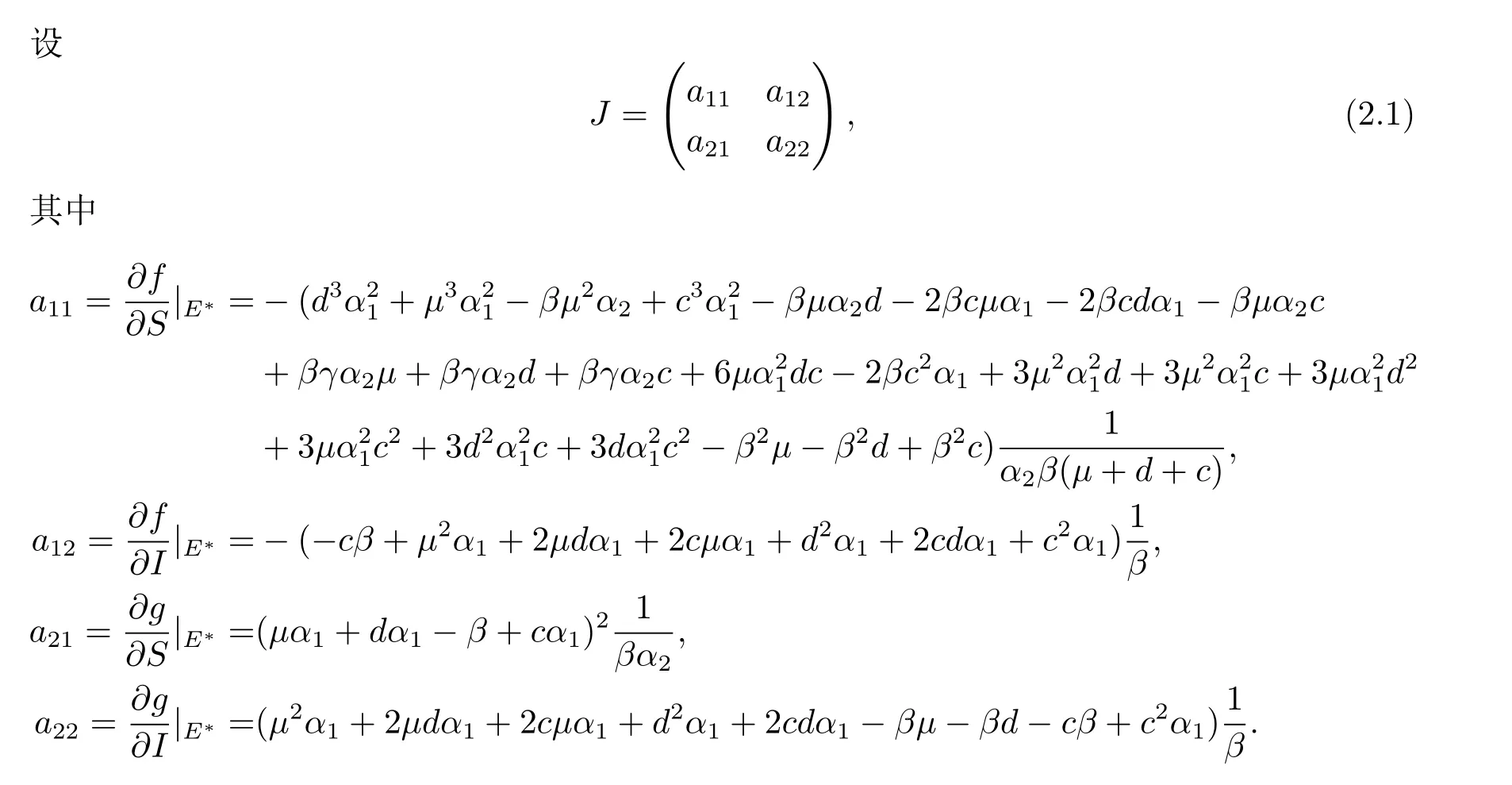
J的特征方程是
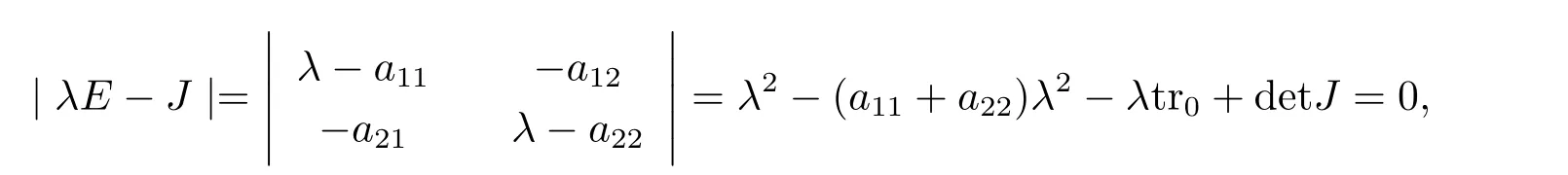
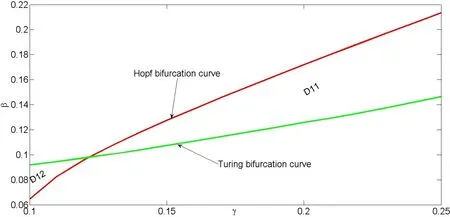
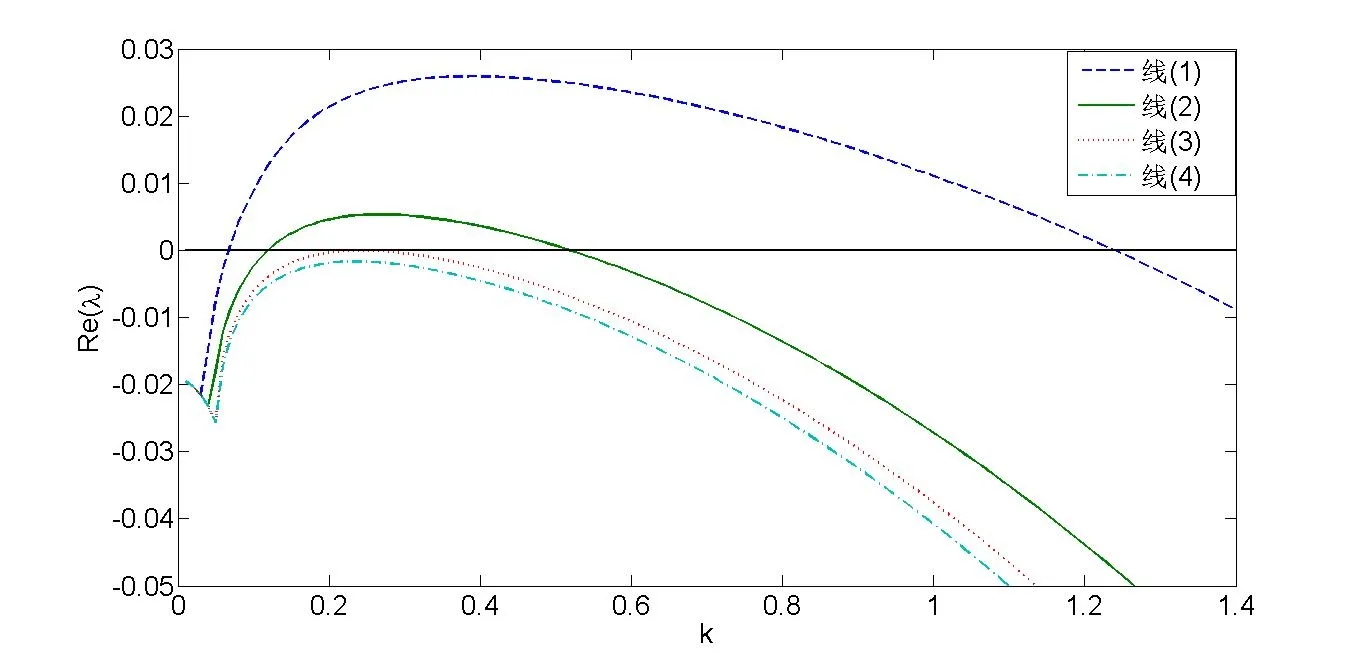
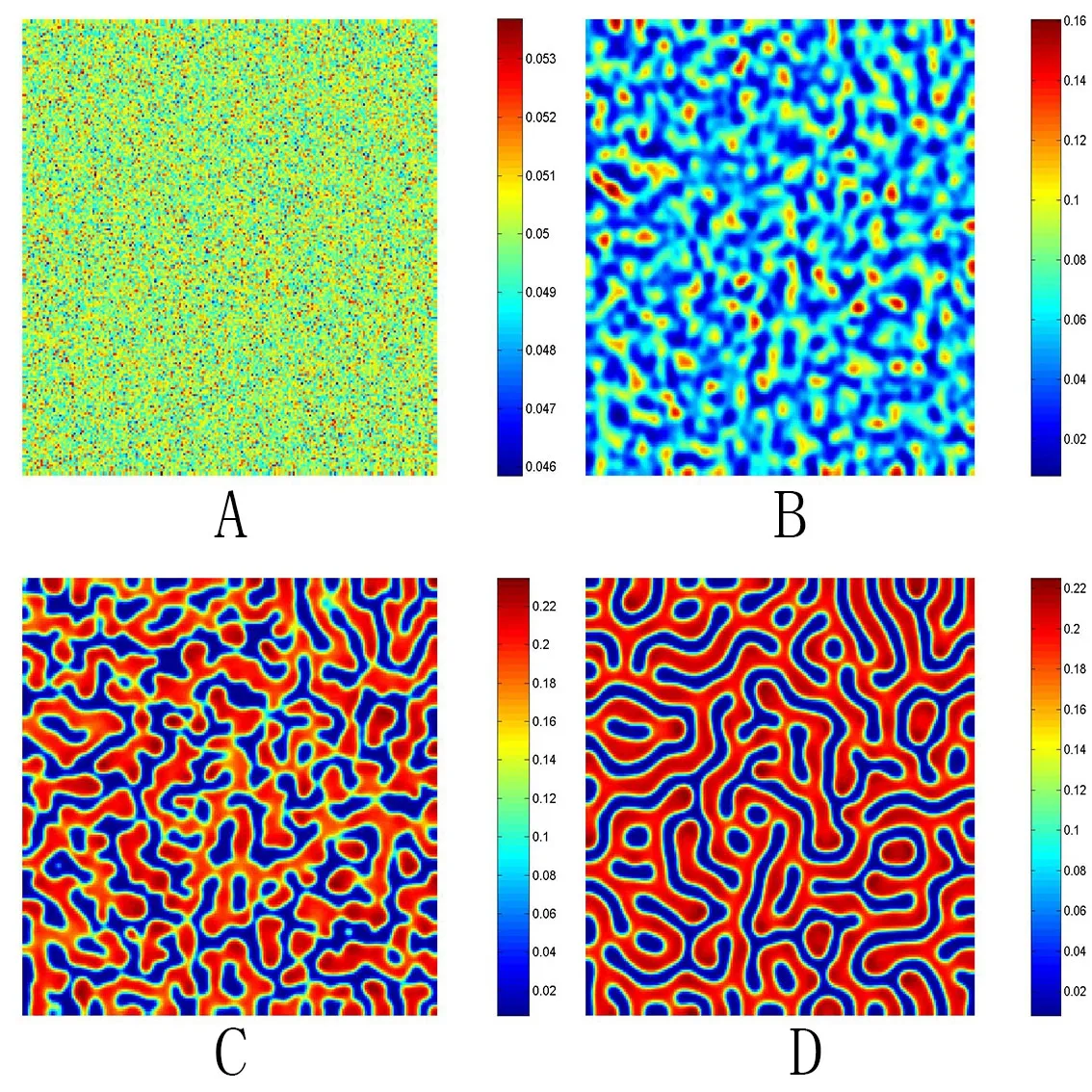
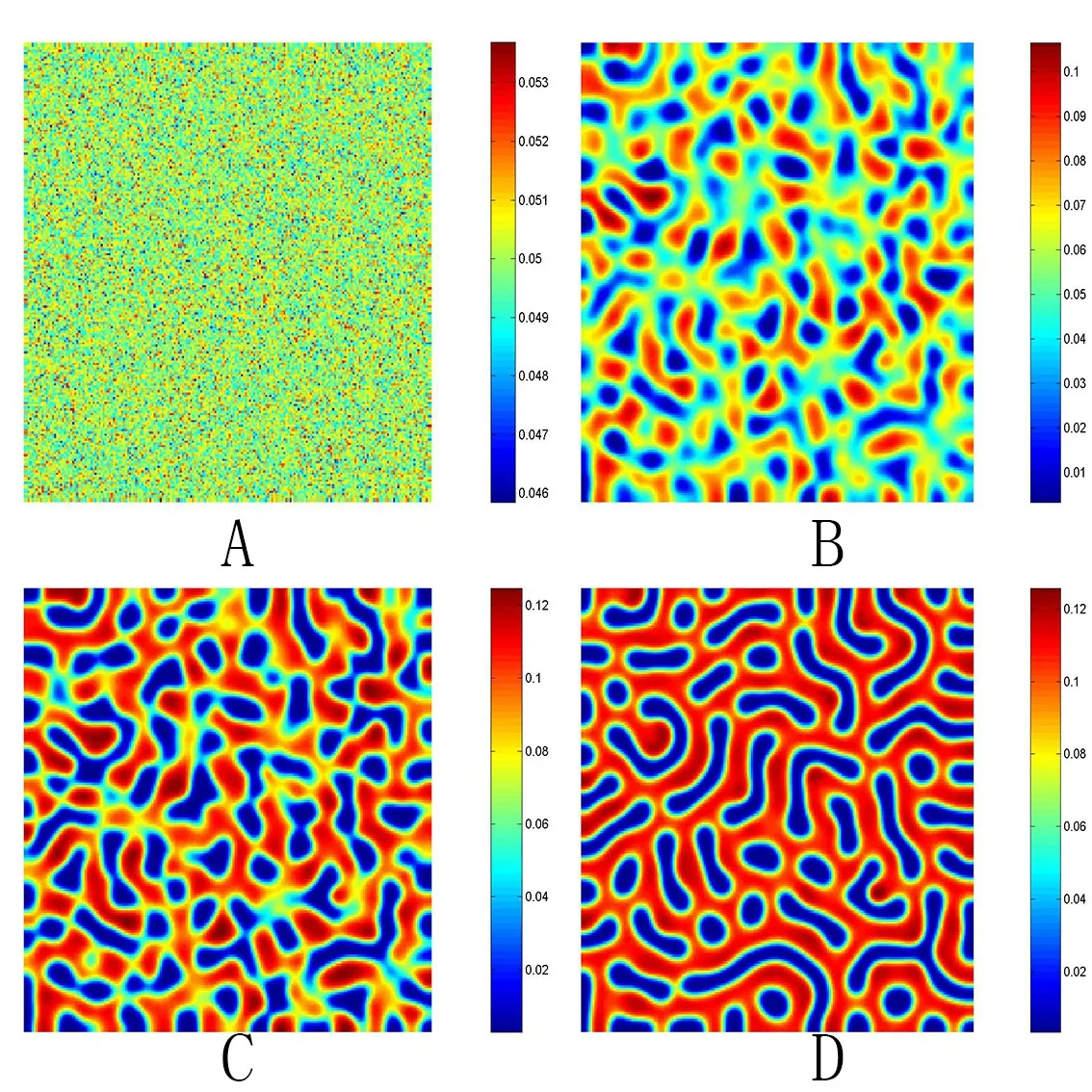
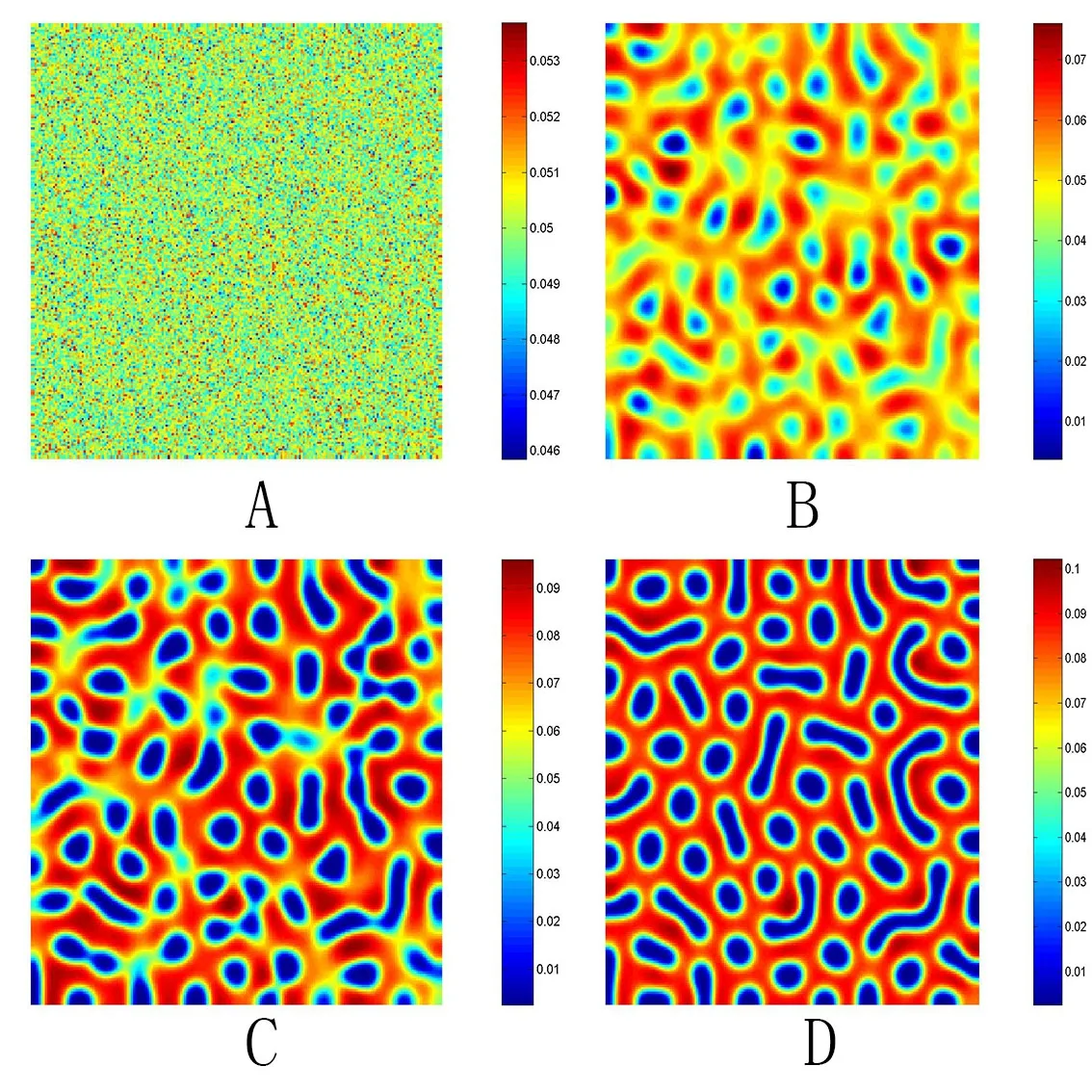
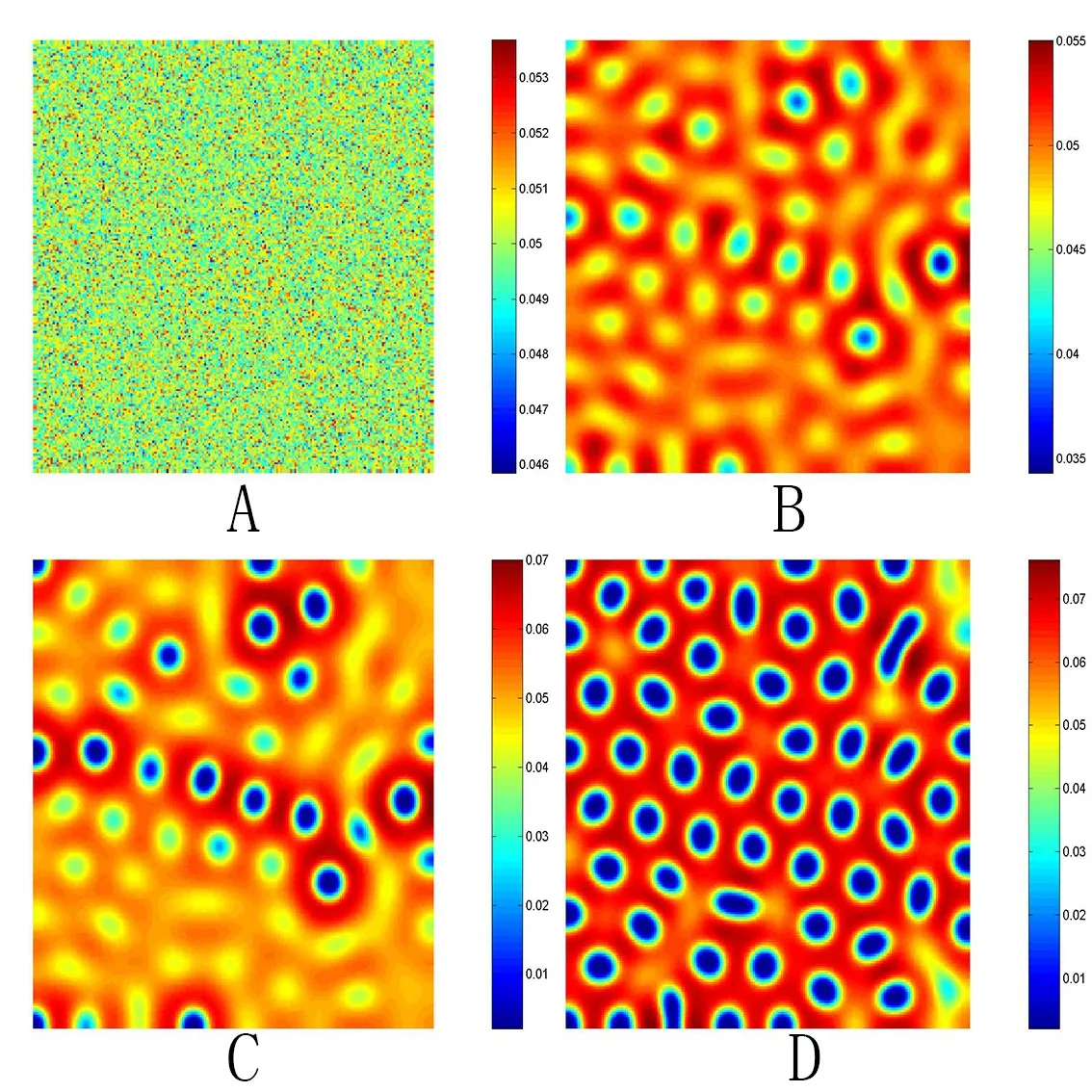
其中tr0=a11+a22,detJ=a11a22?a12a21.易知tr0<0和detJ>0當且僅當max{t1,t3}<β 通過Routh-Hurwitz,可知(S?,I?)是局部漸進穩定的. 現在考慮系統(1.3),并且對平衡點(S?,I?)進行線性化分析.如下面所示,在平衡點(S?,I?) 處作微擾: 這里pλ是在時間t上的擾動增長率;kx和ky是相應的振幅;i是虛數單位并且有i2=?1;k=是波數;S0和I0是兩個正常數.把(2.2)式帶入系統(1.3),并且省略所有的非線性項,可以得到特征方程 特征方程(2.3)的解為如下形式 其中 選擇β作為分支參數.當Im(λk)6=0和Re(λk)=0在k=0時成立,系統出現Hopf分支,這樣能得到Hopf分支曲線 利用穩定性定理[9?11],可知道當Im(λk)=0和Re(λk)=0在k=kT6=0時成立,Turing分支出現,且波數kT滿足因此分支參數βT滿足如下Turing分支曲線 根據Hopf和Turing分支曲線[12,13],能得到Hopf分支區域和Turing不穩定區域. 圖1:模型(1.3)的分支圖,其中d11=0.02,d22=5,d12=0.1,d21=?0.1 在圖1中,可以看到系統(1.3)的分支圖包含了Turing分支線和Hopf分支線,并且它們把γ?β參數空間分成了四個區域,區域D11被稱為Turing空間,在這里發生Turing失穩,區域D12被稱為Hopf空間,在這里發生Hopf失穩. 為了更好地理解參數對系統穩定性的影響作用,在圖2,給出了隨參數d21變化的色散關系圖.線(3)對應著Turing臨界值d21=?1.13,當d21=?0.9>?1.13時,Turing失穩發生;當d21=?1.2 圖2:Re(λ)(特征值λ的實部)和k的關系,γ=0.2,K=1,μ=0.12,d=0.08,c=0.04,α1=0.4,α2=0.5,d11=0.02,d22=5,d12=0.1,β=0.1380和不同的d21:線(1):d21=?0.05;線(2):d21=?0.9;線(3):d21=?1.13;線(4):d21=?1.2 在這一部分,我們將通過Matlab對系統(1.3)進行一系列的數值模擬.所有的數值模擬均運用齊次Neumann邊界條件.將空間區域離散為200×200個格子.對空間的離散采用有限差分法,設定空間步長為?h=0.25,對時間的離散采用歐拉方法,取定時間步長為?t=0.01. 首先設d11=0.02,d22=5,d12=0.1,γ=0.2,μ=0.12,β=0.1380,d=0.08,c=0.04,α1=0.4,α2=0.5.現在研究參數d21的不同值所產生的斑圖. 圖3:時間:(A)t=0;(B)t=20000;(C)t=40000;(D)t=800000 圖4:時間:(A)t=0;(B)t=56000;(C)t=70000;(D)t=490000 在圖3中,d21=?0.05,這時可見:(A)中顏色條數值基本不變,初值選取為平衡解加上一個隨機擾動;(B)中出現類條狀斑圖;(C)中出現條狀斑圖;(D)條狀斑圖幾乎占據了整個區域,且系統的動力學行為不再發生變化. 圖4,圖5分別是d21=?0.7和d21=?0.9時,染病者的時間演化圖.由圖4和圖5可見:隨著時間的演化,最終點狀斑圖和條狀斑圖共存.但圖4中條狀斑圖占優;而當d21達到?0.9時,點狀斑圖會占優(圖5(D)).由圖6可見,當d21增至?1.1時,最終點狀斑圖幾乎占滿整個空間. 圖5:時間:(A)t=0;(B)t=90000;(C)t=120000;(D)t=800000 圖6:時間:(A)t=0;(B)t=520000;(C)t=600000;(D)t=800000 本文研究了在Neumann邊界條件下,負交叉擴散對帶有非線性傳染率的傳染病模型的影響.具體表現為負交叉擴散可引起系統(1.3)在平衡點E?處的Turing失穩,并由此得到了不同類型的斑圖,包括點狀斑圖、條形斑圖和點條混合斑圖.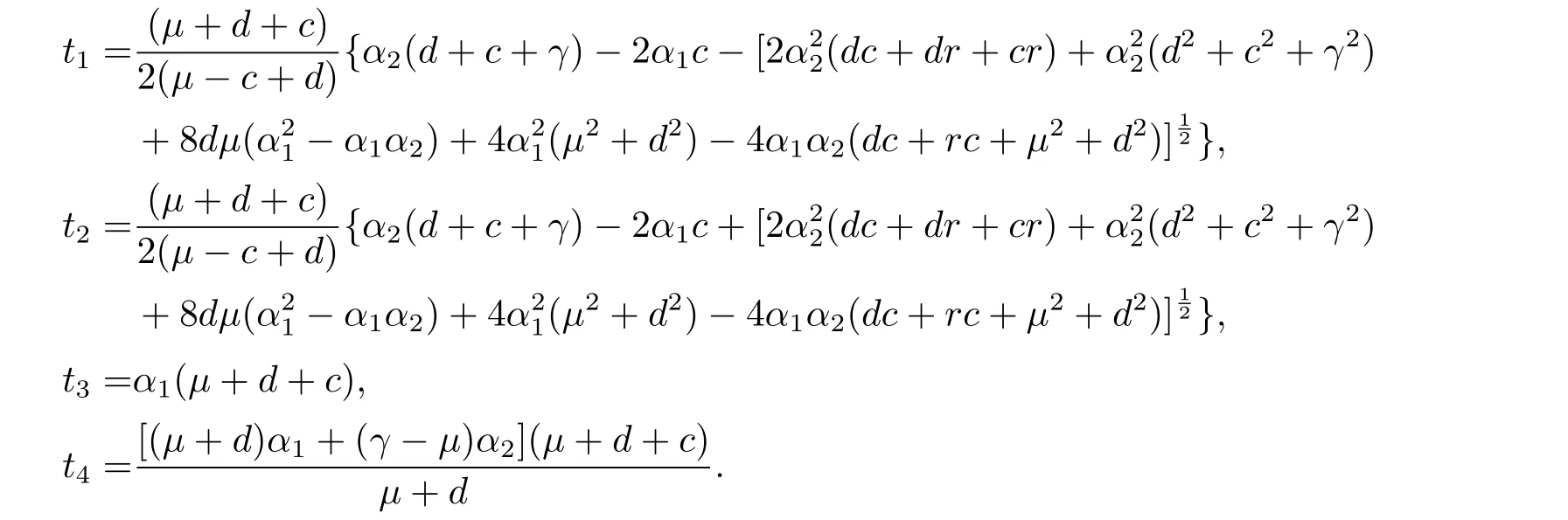
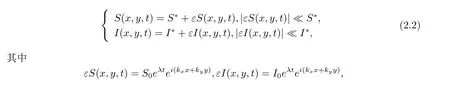
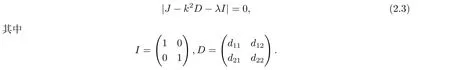

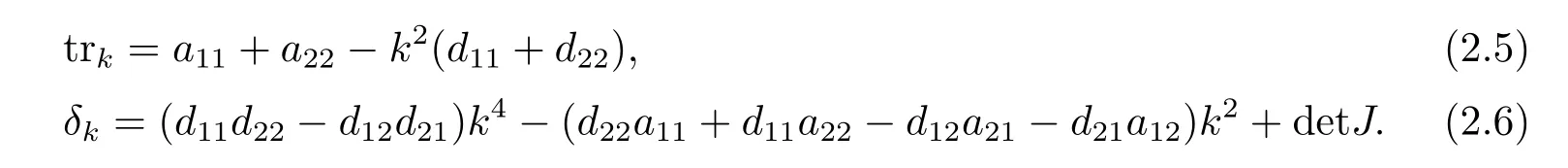


3 數值模擬
4 結論

